 |
Формулы произведения функций
|
|
|
|
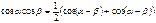
Формулы половинного аргумента
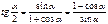
Формулы двойного аргумента
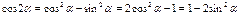
Формула дополнительного угла
где
Определение тригонометрических функций
Универсальная подстановка
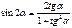
Свойства тригонометрических функций
| Функция | Свойства | |||
| Область определения | Множество значений | Четность-нечетность | Период | |
| cosx | 
| 
| cos(-x)= cosx | |
| sinx |
| 
| sin(-x)= -sinx | |
| tgx | 
| 
| tg(-x)= -tgx | |
| ctgx |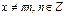 
|
| ctg(-x)= -ctgx | |
Тригонометрические уравнения
Косинус:
Уравнения с синусом
Частные формулы:
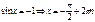
Общая формула:
Уравнения с тангенсом и котангенсом
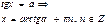
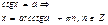
Формулы обратных триг функций
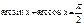
| Если 0 < x £ 1, то arccos(-x) = p - arccosx arcsin(-x) = - arcsinx | Если x > 0, то arctg(-x) = - arctgx arcctg(-x) = p - arcctgx |
Обратные триг функции
| Функция | Свойства | ||
| Область определения | Множество значений | ||
| arccosx | 
| [ 0; p ] | |
| arcsinx |
| [-p/2; p/2] | |
| arctgx | 
| (-p/2; p/2) | |
| arcctgx | 
| (0; p) | |
Геометрия
Теорема косинусов, синусов
Теорема косинусов:
Теорема синусов:
Площадь треугольника
 |  | ||||
 |
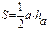
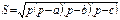
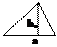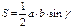
Средняя линия
Средняя линия – отрезок, с соединяющий середины двух с сторон треугольника.
Средняя линия параллельна т третьей стороне и равна е её половине: 
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного
Равносторонний треугольник
треугольник, у которого все стороны равны.
|
|
|
v Все углы равны 600.
v Каждая из высот является одновременно биссектрисой и медианой.
v Центры описанной и вписанной окружностей совпадают.
v Радиусы окружностей: 
Площадь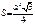 
Равнобедренный треугольник
треугольник, у которого две стороны равны.
1.Углы, при основании треугольника, равны
2.Высота, проведенная из вершины, является б биссектрисой и медиан
|
 |
v Теорема Пифагора: 
Площадь: 
v Тригонометрические соотношения: 
v Центр описанной окружности лежит на середине гипотенузы.
v Радиусы окружностей: 
v Высота, опущенная на гипотенузу: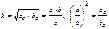 
v Катеты: 
Основные соотношения в треугольнике
Ø Неравенство треугольника:
a + b > c; a + c > b; b + c > a
Ø Сумма углов:
Ø Против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
Ø 
Против равных сторон лежат равные углы, и обратно, против равных углов лежат равные стороны.
Биссектриса
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
· Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам: ab: ac = b: c
· Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
· 
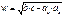
Конус
|
|
 |
Усеченный конус
 |
 |
Вписанная окружность
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
- Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой:
a + b = c + d
Описанная окружность
Касательная, секущая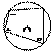 
·
· Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
|
|
|
· Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
· Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
· Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой: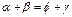 
Длина окружности, площадь
 |
 |
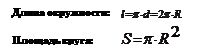
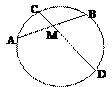Хорда
Хорда – отрезок, соединяющий две точки окружности.
· Диаметр, делящий хорду пополам, перпендикулярен хорде.
· В окружности равные хорды равноудалены от центра окружности.
· Отрезки пересекающихся хорд связаны равенством:
Шар
 |
 |
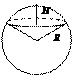Шаровой сектор
Шаровой сегмент
Центральный, вписанный угол
Сектор
 |
Касательная, секущая
 |
Касательная – прямая, имеющая с окружностью одну общую точку.
Секущая – прямая, имеющая с окружностью две общие точки.
X 
X 
X 
Призма
Прямая
Призма
Цилиндр
Медиана
 |
Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
· Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершины треугольника).
· Медиана делит треугольник на два треугольника с равными площадями.
Правильная пирамида
Правильная пирамида
пирамида, у которой в основании и правильный многоугольник, а вершина с м проецируется в центр основания.
М Все боковые рёбра равны между м м собой и все боковые грани – равные м равнобедренные треугольники.
Усеченная пирамида
Скалярное произведение
 |
Сумма, разность векторов
Углы на плоскости
 |
|
|
|
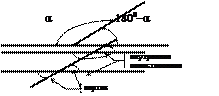