 |
Перевод чисел из одной системы счисления в другую.
|
|
|
|
Министерство образования и науки Российской Федерации
ФГБОУ ВПО «Тульский государственный университет»
Технический колледж имени С.И. Мосина


МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К практическим и самостоятельным работам
по дисциплине
«Информатика»
по специальности
Компьютерные системы и комплексы
Программирование в компьютерных системах
(углубленная подготовка)
Тула 2014
Цикловой комиссий информационных технологий | ||
| Протокол от «__»_________20____ г. №_____ | ||
| Председатель цикловой комиссии И.В.Миляева |
| Авторы: | |
Практическая работа № 1
Тема: Представление информации в двоичной системе счисления.
Представление информации в различных системах счисления.
1. Цель работы: научиться переводить числа из одной системы счисления в другую.
Краткие теоретические сведения. Примеры решения заданий.
Система счисления – это совокупность правил для обозначения и наименования чисел.
Непозиционной называется такая система счисления, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.
Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Наименование системы счисления соответствует ее основанию (например, десятичной называется система счисления так потому, что ее основание равно 10, т.е. используется десять цифр).
Система счисления называется позиционной, если значение цифры зависит от ее места (позиции) в записи числа.
Системы счисления, используемые в компьютерах
|
|
|
Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.
Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7.
Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F.
Перевод чисел из одной системы счисления в другую.
Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
Примеры:
III (3), IV (4), XXII (22), XLI (41), LXXXIII (83)
Количество цифр применяемых в позиционной системе счисления называется основанием системы счисления p. Местоположение символа в числе называется разрядом, каждый разряд имеет свой вес.
В любой системе счисления число можно представить
Аn An-1 … A2 A1 A0, A--1 A-2 … A—m= An *pn + An-1 *pn-1 +…+ A2 *p2 + A1 *p1 + A0 *p0 + A-1 *p-1 + A-2 *p-2 +…+ A-m *p-m
Например:
345,16(10) = 3 * 102 + 4 * 101 + 5 * 100 + 1 * 10-1 * 6 * 10-2,
где (10) - основание десятичной системы счисления.
Наиболее употребляемыми в настоящее время позиционными системами являются:
|
|
|
2 — двоичная (в дискретной математике, информатике, программировании);
3 — троичная;
8 — восьмеричная;
10 — десятичная (используется повсеместно);
12 — двенадцатеричная (счёт дюжинами);
13 — тринадцатеричная;
16 — шестнадцатеричная (используется в программировании, информатике);
60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).
В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.
В вычислительной технике при кодировании информации широко используются двоичная, восьмеричная и шестнадцатиричная системы счисления, которые представлены в таблице 1.
Таблица 1
| Система счисления | |||
| двоичная | восмиричная | десятичная | шестнадцатиричная |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Чтобы перевести число из одной системы счисления в другую необходимо разделить его на основание той системы в которую оно переводится, полученный остаток будет младшим разрядом числа в новой системе счисления, частное от деления делится на основание, остаток - следующий разряд и так далее, деление продолжается до тех пор пока не получится частное меньше основания системы в которую мы переводим - это будет старший разряд число в новой системе счисления.
Например, перевести число 351 из десятичной системы счисления в шестнадцатиричную и двоичную:

351(10) = 15F(16)
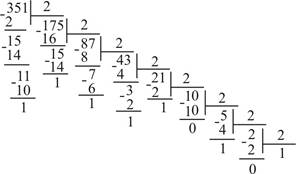
351(10) = 101011111(2)
Для перевода чисел из двоичной системы счисления в восьмеричную, шестнадцатиричную и наоборот можно воспользоваться следующим правилом: группа цифр из 3-х, 4-х двоичной системы заменяется на соответствующую цифру для восьмеричной, шестнадцатиричной системы и наоборот в соответствии с таблицей 2.
Например:
110 111 100 001(2) = 6741(8)
2305(8) = 010 011 000 101(2)
1111 0000 1011(2) = F0B(16)
577(16) = 0101 0111 0111(2)
Таблица 2
|
|
|
| Система счисления | |||
| двоичная | восьмиричная | двоичная | шестнадцатиричная |
| - | - | ||
| - | - | ||
| - | - | А | |
| - | - | В | |
| - | - | С | |
| - | - | D | |
| - | - | E | |
| - | - | F |
Задание
Таблица заданий:
Перевести:
- из двоичной в восьмиричную и 16-ричную;
- из восьмиричной в двоичную и 16-ричную;
- из десятичной в двоичную, восьмиричную и 16-ричную;
- из 16-ричной в двоичную, восьмиричную и десятиричную.
| Система счисления | ||||
| nn | Двоичная | Восьмиричная | Десятичная | 16-иричная |
| A4C2 | ||||
| A136 | ||||
| 9CA9 | ||||
| 5BA8 | ||||
| 6F89 | ||||
| 371A | ||||
| A625 | ||||
| 9D56 | ||||
| 2A71 | ||||
| CADA | ||||
| CCD9 | ||||
| 4EEA | ||||
| AB65 | ||||
| AAA1 | ||||
| 19D2 | ||||
| CF1F | ||||
| D098 | ||||
| D5B3 | ||||
| AE66 | ||||
| 786B | ||||
| B4FA | ||||
| BEBD | ||||
| 112D | ||||
| 1C82 |
4. Контрольные вопросы
1. Что такое система счисления?
2. Что такое основание системы счисления?
3. Что такое непозиционная система счисления?
4. Что такое позиционная система счисления?
5. Из каких знаков состоит алфавит десятичной и двоичной систем?
6. Почему в вычислительной технике взята за основу двоичная система счисления?
7. Какое наибольшее десятичное число можно записать тремя цифрами:
· в двоичной системе;
· в восьмеричной системе;
· в шестнадцатеричной системе?
Практическая работа № 2
|
|
|


