Вычислить неопределенные интегралы:

Контрольная работа по математике.

Вариант № 8

 

1. Вычислить пределы функций:

1) 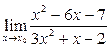; если х₀ = - 2; х₀ = - 1; х₀ = ¥

2)

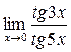
3)

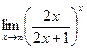
4)

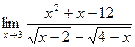
Решение:

1) ;

Получили неопределенность. Разложим числитель и знаменатель на множители:

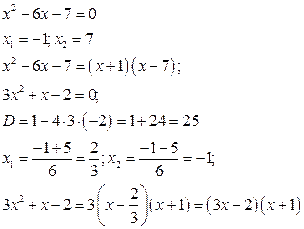
Тогда

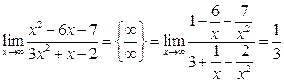
2)

Применили следствие из первого замечательного предела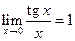

3)

Здесь применили второй замечательный предел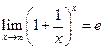

4)

 

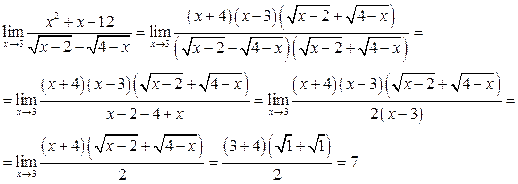
Найти производные функций:

1)

2)

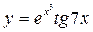
3)

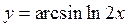
Решение:

1) По правилу дифференцирования частного 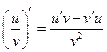и сложной функции получим:

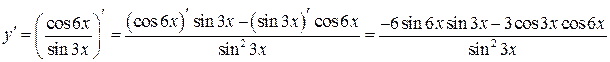
2) По правилу дифференцирования произведения 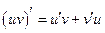получим

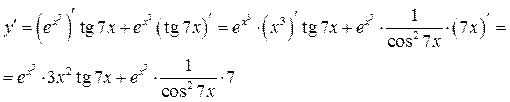
3) По правилу дифференцирования сложной функции

3. Исследовать свойства функции и построить её график:

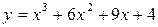
Решение:

1) Областью определения данной функции являются все действительные значения аргумента х, то есть D(y): 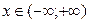, а это значит, что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных асимптот.

2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

Решая полученное квадратное уравнение по формулам Виетта, делаем вывод о том, что функция имеет две критические точки .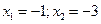

Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:

x		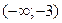-3	(-3;-1)	-1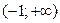
	+		-		+
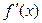
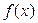
	&	max	(	min	&

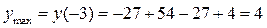
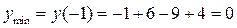
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем II производную заданной функции и приравняем ее к нулю:

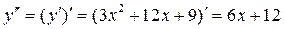
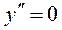, т.е.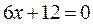

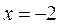
Итак, функция имеет одну критическую точку .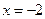

Разобьем область определения полученной точкой на части, в каждой из которой установим знак II производной:

x		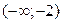-2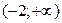
	-		+
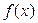
		т.п.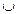

Значение 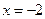является абсциссой точки перегиба графика функции,

ордината этой точки:

4) Выясним наличие у графика заданной функции наклонных асимптот.

Для определения параметров уравнения асимптоты воспользуемся формулами: .

Имеем .

Таким образом, у графика заданной функции наклонных асимптот нет.

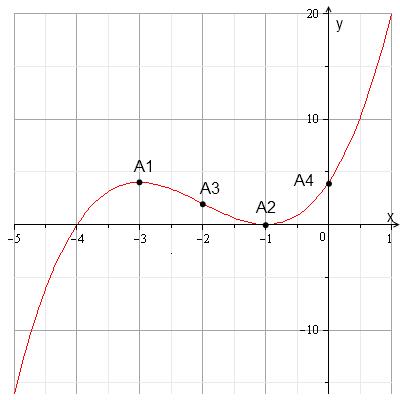
5) Для построения графика в выбранной системе координат изобразим точки:

максимума А₁(-3; 4),

минимума А₂(-1; 0),

перегиба А₃ (-2; 2)

точку пересечения графика с осью Оу А₄ (0; 4).

С учетом результатов предыдущих исследований построим кривую.

Вычислить неопределенные интегралы:

1)

2)

Решение:

1)

 

 

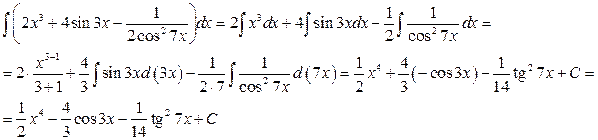
2)

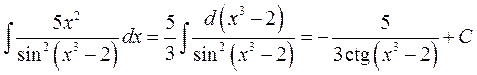
5. Вычислить интеграл методом средних прямоугольников и методом трапеций с шагом n = 10. Определить погрешность вычислений. Сравнить результаты.

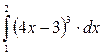
Решение:

1) Составим таблицу, вычислив предварительно значения каждой колонки

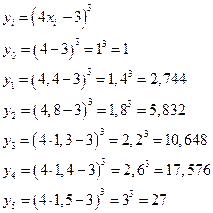
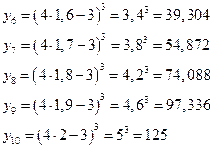
Составим таблицу

i	xi	yi
	1,1	2,744
	1,2	5,832
	1,3	10,648
	1,4	17,576
	1,5
	1,6	39,304
	1,7	54,872
	1,8	74,088
	1,9	97,336

2) Вычислим интеграл методом средних прямоугольников.

 

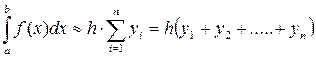
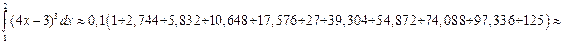
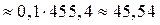
3) Вычислим интеграл методом трапеций

 

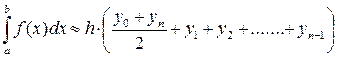
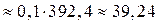
4) Вычислим точное значение интеграла

 

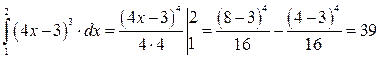
5) Вычислим погрешности

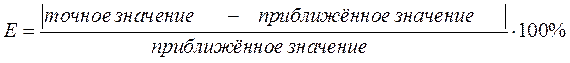
метод средних прямоугольников:

 

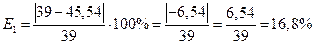
метод трапеции:

 

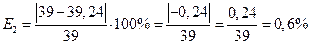
6. Вычислить площадь фигуры, ограниченной параболами:

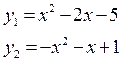
Решение:

1) Сделаем чертеж парабол:

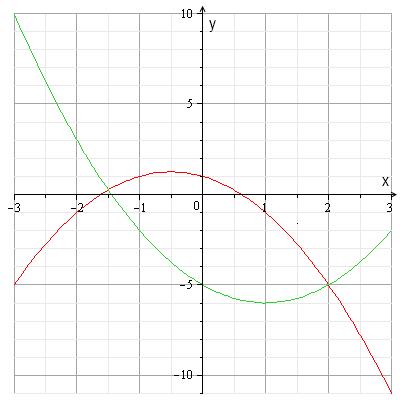
2) Найдем абсциссы точек пересечения заданных парабол.

Для этого приравняем правые части их уравнений: .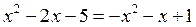

Решаем полученное квадратное уравнение:

.

Вычисление площади фигуры осуществляем по формуле

,

где 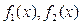- кривые, ограничивающие фигуру .

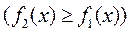В нашем случае

7. Решить дифференциальные уравнения:

1) Найти частное решение дифференциального уравнения

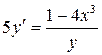, если y₀ = 3 при x₀ = 1

2) Найти общее решение дифференциального уравнения второго порядка:

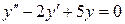
Решение:

1)

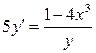
Преобразуем данное уравнение:

Мы получили дифференциальное уравнение первого порядка с разделенными переменными.

Представим 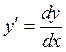, получим

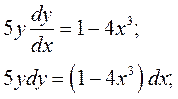
Проинтегрируем обе части уравнения:

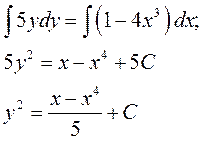
Нашли общее решение дифференциального уравнения, где С – произвольная постоянная.

Определим значение С, для этого подставим в общее решение дифференциального уравнения значения х₀ и у₀.

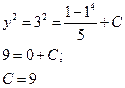
Итоговый ответ: 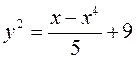или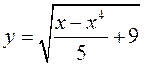

2)

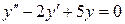
Для заданного дифференциального уравнения составим соответствующее характеристическое уравнение 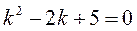по принципу: .

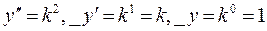Решим полученное квадратное уравнение :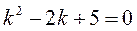

Получили два различных комплексных числа 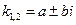, тогда общее решение данных уравнений записывается в виде: .

В нашем случа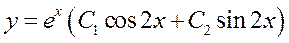е , где 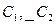- произвольные постоянные.

 

Список использованной литературы

1. Богомолов Н.В. Математика: учеб. для ссузов. - М.: Дрофа, 2006. - 395 с.

2. Богомолов Н.В. Практические занятия по математике. - М.: Высш. шк., 2002. - 495 с.

3. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2003. - 208 с.

4. Валуцэ И.И. Математика для техникумов. – М.: Наука. Гл. ред. Физ.мат. лит., 1990 – 576 с.: ил.

5. Пехлецкий И.Д. Математика. - М.: Издательский центр "Академия", 2002. - 304 с.

6. Соловейчик И.Л. Сборник задач по математике с решениями для техникумов. - М.: ООО "Издательский дом "ОНИКС 21 век", 2003. - 464 с.

Поделиться:

Воспользуйтесь поиском по сайту: