Расчет рамно-балочных систем

Министерство образования и науки

Российской Федерации

Казанский государственный архитектурно-строительный университет

Кафедра строительной механики

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к расчетно-графической работе

“Расчет рамно-балочных систем

на устойчивость”

 

 

Казань

УДК 624.04 (075)

ББК 38.112

Ш17

 

 

Ш17 Методические указания к расчетно-графической работе “Расчет рамно-балочных систем на устойчивость” / Составители Р.А. Шакирзянов, Ф.Р. Шакирзянов. – Казань: КГАСУ, 2011. – 16 с.

 

Печатается по решению редакционно-издательского совета Казан-ского государственного архитектурно-строительного университета.

 

Методические указания предназначены для успешного усвоения теоретических знаний, закрепления навыков по расчету сооружений на устойчивость и выполнения расчетно-графической работы (РГР) по устойчивости сооружений.

Определяются общая схема и последовательность выполнения РГР, даются рекомендации для ее самостоятельного выполнения и примеры решения задач расчета рамно-балочных систем на устойчивость методом перемещений.

 

Ил. 8, табл. 4

 

 

Рецензент

 

Кандидат физико-математических наук, профессор кафедры теоретической механики КГАСУ

А.З. Камалов

 

УДК 624.04(075)

ББК 38.112

 

 

Ó Казанский государственный

архитектурно-строительный

университет, 2011

 

Ó Шакирзянов Р.А., Шакирзянов Ф.Р.,

ОБЩИЕ ПОЛОЖЕНИЯ

Строительная механика − это наука о принципах и методах расчета сооружений на прочность, жесткость и устойчивость. Поэтому бакалавры и магистры, обучающиеся по направлению “Строительство” и изучающие курс строительной механики, а также аспиранты и специалисты-строители, повышающие квалификацию по этому направлению должны знать теоретические положения, принципы и методы расчета сооружений на устойчивость.

Под воздействием внешней нагрузки в рамно-балочных системах (рис. 1 а) могут возникать большие продольные усилия (рис. 1 б), приводящие к потере устойчивости системы. В таких случаях (рис. 1 в), а также при узловом воздействии нагрузки (рис. 1 г) может ставиться задача проверки этих систем на устойчивость.

Рис. 1

Обе эти задачи можно решать методом перемещений по единой методике, если принять упрощающие гипотезы:

– нагрузка прикладывается только в узлах;

– продольные силы вызывают только центральное сжатие;

– при потере устойчивости напряжения остаются в упругой зоне;

– деформации малы и расстояния между узлами сохраняются.

Алгоритм расчета на устойчивость методом перемещений

1. Определение числа неизвестных.

2. Выбор основной системы.

3. Построение эпюры продольных сил N ₀ в основной системе.

4. Определение параметров устойчивости стержней

.

Все параметры устойчивости необходимо выразить через максимальный из них и обозначить v=max v_i , а остальные определить как , где коэффициенты .

5. Запись канонических уравнений.

6. Рассмотрение единичных состояний основной системы.

7. Построение эпюр изгибающих моментов в единичных состояниях.

8. Определение коэффициентов канонических уравнений.

9. Решение уравнения устойчивости .

10. Определение критических сил и приведенных длин сжатых стержней по формулам

, .

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. На одноэтажную раму действует сосредоточенная сила, направленная вдоль оси одной из стоек (рис. 2 а). Определить величину этой силы, при которой рама достигает критического состояния.

Рис. 2

Решение.

1. Определяем число неизвестных по методу перемещений:

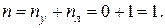
2. Выбираем основную систему (рис. 2 б).

3. Строим эпюру продольных сил в основной системе (рис. 2 в).

4. Параметры устойчивости стержней:

, .

5. Каноническое уравнение будет

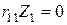
(так внешняя нагрузка до момента потери устойчивости не вызывает изгиба элементов, то ).

6. Рассмотрим единичное состояние основной системы (рис. 3 а).

7. В единичном состоянии строим эпюру изгибающих моментов. При этом надо помнить следующее: в стержне 3 в основной системе имеется сжимающие усилие (рис. 2 в), поэтому при построении эпюры изгибающих моментов в этом стержне надо пользоваться специальной таблицей метода перемещений (табл. 2 в приложении), а в стержнях 1 и 2 сжимающие силы отсутствуют, поэтому при построении эпюр моментов в этих стержнях надо использовать обычную таблицу метода перемещений (табл. 3). Тогда эпюра моментов для стержня 3 будет криволинейной, а для стержня 1 будет прямолинейной (рис. 3 б). Следует отметить, что в данной задаче построение этой эпюры не обязательно.

Рис. 3

8. По рис. 3 в определяем коэффициент канонического уравнения:

.

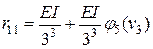9. Каноническое уравнение 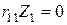имеет два решения:

1) , 2) .

Согласно основной системе (рис. 2 б), второе решение соответствует закреплению 3-го стержня в горизонтальном направлении. Поэтому этот стержень, подвергнутый воздействию сжимающей силы P, можно рассматривать отдельно (рис. 3 г).

Такие задачи решаются теоретически, результаты их расчета приведены в приложении в табл. 1. Нашему случаю соответствует 4-ая схема этой таблицы, из которого определяем коэффициент приведенной длины стержня μ=0,7. Тогда

.

Если рассматривать первое решение, то

.

Из него получаем уравнение 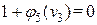или .

Тогда, используя табл. 4, определяем корень уравнения .

Итак, получили два решения: 1) , 2) . По критерию Эйлера, критической является наименьшая из них. Поэтому .

10. Определяем величину критической силы и коэффициент приведенной длины стержня. Принимая

,

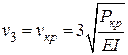получаем

, .

Как видно из данного примера, уравнение дает завышенное значение приведенной длины стержня (а значит и критической силы). При решении других задач получаются аналогичные результаты. Поэтому в дальнейшем решения типа рассматривать не будем.

 

Задача 2. Провести расчет рамы, представленной на рис. 4 а, на устойчивость методом перемещений.

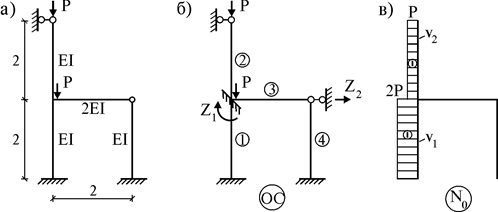
Рис. 4

Решение.

1. Определяем число неизвестных по методу перемещений:

2. Выберем основную систему (ОС). Она получается введением двух условных связей − заделки и опоры (рис. 4 б).

3. Строим эпюру продольных сил в основной системе (рис. 4 в). В ней имеются два стержня, в которых есть сжимающие продольные усилия.

4. Параметры устойчивости стержней рамы будут:

, , .

Наибольший из них соответствует 1-му стержню. Поэтому примем его параметр устойчивости за основной и обозначим

.

Так как

,

имеем .

5. Запишем систему канонических уравнений:

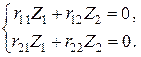
Эта однородная система уравнений имеет два решения:

1) 2) .

Второе решение, как дающее завышенное значение критического корня, рассматривать не будем. А первое решение с учетом принимает вид

.

Это и есть уравнение устойчивости.

6. Рассмотрим два единичных состояния основной системы, в которых обозначим деформации элементов и реактивные усилия (рис. 5):

Рис. 5

7. Используя таблицы метода перемещений, в обоих состояниях строим эпюры изгибающих моментов (рис. 6 а, б).

Рис. 6

При этом при построении эпюр в стержнях 1 и 2 (в них учитывается сжатие) основной системы используем специальную таблицу метода перемещений (табл. 2), а при построении эпюр в стержнях 3 и 4 (где сжимающие силы отсутствуют) используем обычную таблицу метода перемещений (табл. 3). Поэтому эпюры моментов для стержней 1 и 2 них будут криволинейными, а для стержней 3 и 4 − прямолинейными.

8. Коэффициенты системы канонических уравнений определяем согласно единичным состояниям (рис. 5) и по рис. 6 а, б:

;

;

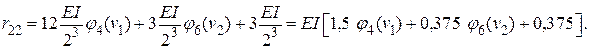
9. Решаем уравнение устойчивости. Для этого подставим найденные коэффициенты в уравнение устойчивости и сократим его на EI. Получим трансцендентное уравнение (уравнение с бесконечным числом корней). С целью определения наименьшего положительного корня этого уравнения вначале определим интервал, в котором этот корень находится. Для этого проведем следующие рассуждения:

1) уравнение устойчивости зависит от параметра устойчивости 1-го стержня рамы , поэтому исследуем поведение этого стержня;

2) в состоянии “малой жесткости” рамы, когда изгибные жесткости всех стержней (кроме 1-го) равны нулю (рис. 7 а), стержень 1 можно рассматривать отдельно как показано на рис. 7 б. В этом случае по табл. 1 имеем . Тогда ;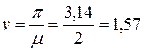

Рис. 7

3) в состоянии “большой жесткости”, когда изгибные жесткости всех стержней (кроме 1-го) равны бесконечности (рис. 7 в), стержень 1 можно рассматривать отдельно как показано на рис. 7 г. По табл. 1 принимаем . Тогда, ;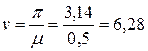

4) в действительности жесткость 1-го стержня находится в интервале от нуля до бесконечности. Следовательно, искомый корень уравнения устойчивости находится между найденными крайними величинами, т.е.

.

Теперь уточним его. Это удобно проводить в следующей табличной форме (значения специальных функций берутся из табл. 4):

3,0	2,1	0,656	0,660	5,301	0,839	-0,764	0,089	-0,810	0,205	0,503
4,0	2,8	0,293	0,294	4,028	0,696	-0,823	-0,637	-2,319	-1,450	-6,520
3,2	2,2	0,599	0,620	5,130	0,815	-0,758	-0,038	-0,993	-0,055	-0,854
3,1	2,2	0,629	0,620	5,188	0,828	-0,776	0,027	-0,993	0,043	-0,380

При заполнении этой таблицы вначале в найденном интервале определяются точки, между которыми функция меняет свой знак. Например, при 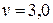имеем , а при имеем . Значит, критический корень уравнения лежит в этом интервале (рис. 8 а). Далее, поэтапно сужая интервал, устанавливаем, что искомый критический корень уравнения устойчивости лежит в интервале 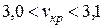. При необходимости проводим интерполяцию (рис. 8 б) и принимаем .

Рис. 8

10. Определяем критические силы и приведенные длины сжатых стержней:

, .

, .

П Р И Л О Ж Е Н И Е

Таблица 1. Коэффициенты приведенных длин прямых стержней

 

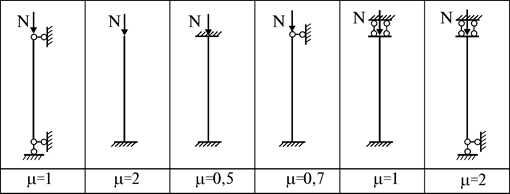
Таблица 2. Реакции сжатого стержня от единичных перемещений

(специальная таблица метода перемещений)

Таблица 3. Реакции стержня от единичных перемещений

(обычная таблица метода перемещений)

 

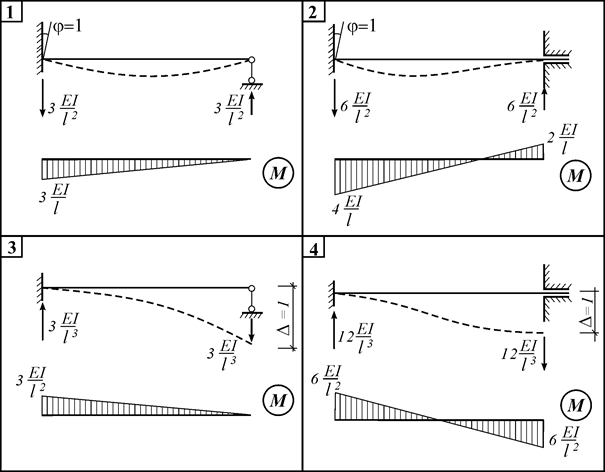
Таблица 4. С пециальные функции метода перемещений и их значения

 

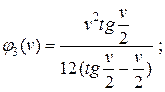
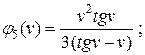
Значения этих функций в интервале 0÷2π см. на стр. 14-15:

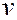
0,0
0,1	0,9997	1,0002	0,9998	0,9990	0,9993	0,9960
0,2	0,9987	1,0007	0,9993	0,9960	0,9973	0,9840
0,3	0,9970	1,0015	0,9985	0,9910	0,9940	0,9640
0,4	0,9947	1,0027	0,9973	0,9840	0,9893	0,9360
0,5	0,9916	1,0042	0,9958	0,9750	0,9832	0,8999
0,6	0,9879	1,0061	0,9940	0,9640	0,9757	0,8557
0,7	0,9836	1,0083	0,9918	0,9510	0,9669	0,8035
0,8	0,9785	1,0109	0,9893	0,9360	0,9565	0,7432
0,9	0,9727	1,0138	0,9864	0,9189	0,9447	0,6747
1,0	0,9662	1,0172	0,9832	0,8999	0,9313	0,5980
1,1	0,9590	1,0209	0,9797	0,8788	0,9164	0,5131
1,2	0,9511	1,0251	0,9757	0,8557	0,8998	0,4198
1,3	0,9424	1,0297	0,9715	0,8307	0,8814	0,3181
1,4	0,9329	1,0348	0,9669	0,8035	0,8613	0,2080
1,5	0,9227	1,0403	0,9619	0,7744	0,8393	0,0893
π/2≈1,57	0,9149	1,0445	0,9581	0,7525	0,8225
1,6	0,9116	1,0463	0,9565	0,7432	0,8152	–0,0381
1,7	0,8998	1,0529	0,9508	0,7100	0,7891	–0,1743
1,8	0,8871	1,0600	0,9447	0,6747	0,7606	–0,3194
1,9	0,8735	1,0676	0,9382	0,6374	0,7297	–0,4736
2,0	0,8590	1,0760	0,9313	0,5980	0,6961	–0,6372
2,1	0,8436	1,0849	0,9241	0,5566	0,6597	–0,8103
2,2	0,8273	1,0946	0,9164	0,5131	0,6202	–0,9931
2,3	0,8099	1,1051	0,9083	0,4675	0,5772	–1,1861
2,4	0,7915	1,1164	0,8998	0,4198	0,5304	–1,3896
2,5	0,7720	1,1286	0,8908	0,3700	0,4793	–1,6040
2,6	0,7513	1,1417	0,8814	0,3181	0,4234	–1,8299
2,7	0,7295	1,1559	0,8716	0,2641	0,3621	–2,0679
2,8	0,7064	1,1712	0,8613	0,2080	0,2944	–2,3189
2,9	0,6819	1,1878	0,8505	0,1497	0,2195	–2,5838
3,0	0,6560	1,2057	0,8393	0,0893	0,1361	–2,8639
3,1	0,6287	1,2251	0,8275	0,0267	0,0424	–3,1609
π ≈3,14	0,6168	1,2337	0,8225			–3,2899
3,2	0,5997	1,2462	0,8152	–0,0381	–0,0635	–3,4769
3,3	0,5691	1,2691	0,8024	–0,1051	–0,1847	–3,8147
3,4	0,5366	1,2940	0,7891	–0,1743	–0,3248	–4,1781
3,5	0,5021	1,3212	0,7751	–0,2457	–0,4894	–4,5727
3,6	0,4655	1,3509	0,7606	–0,3194	–0,6862	–5,0062
3,7	0,4265	1,3834	0,7455	–0,3954	–0,9270	–5,4904
3,8	0,3850	1,4191	0,7297	–0,4736	–1,2303	–6,0436
3,9	0,3407	1,4584	0,7133	–0,5542	–1,6269	–6,6969
4,0	0,2933	1,5019	0,6961	–0,6372	–2,1726	–7,5060
4,1	0,2424	1,5501	0,6783	–0,7225	–2,9802	–8,5836
4,2	0,1878	1,6037	0,6597	–0,8103	–4,3156	–10,196
4,3	0,1287	1,6636	0,6404	–0,9005	–6,9947	–13,158
4,4	0,0648	1,7310	0,6202	–0,9931	–15,327	–21,780
4,4934	0,0000	1,8017	0,6006	–1,0820	–∞/+∞	–∞/+∞
4,5	–0,0048	1,8070	0,5991	–1,0884	227,93	221,18
4,6	–0,0809	1,8933	0,5772	–1,1861	14,669	7,6160
4,7	–0,1645	1,9920	0,5543	–1,2865	7,8186	0,4553
3 π /2≈4,71	–0,1755	2,0051	0,5514	–1,2991	7,4038
4,8	–0,2572	2,1056	0,5304	–1,3896	5,4023	–2,2777
4,9	–0,3607	2,2375	0,5054	–1,4954	4,1463	–3,8570
5,0	–0,4772	2,3923	0,4793	–1,6040	3,3615	–4,9719
5,1	–0,6099	2,5757	0,4520	–1,7155	2,8130	–5,8570
5,2	–0,7629	2,7960	0,4234	–1,8299	2,3986	–6,6147
5,3	–0,9422	3,0648	0,3935	–1,9474	2,0668	–7,2965
5,4	–1,1563	3,3989	0,3621	–2,0679	1,7884	–7,9316
5,5	–1,4182	3,8236	0,3291	–2,1917	1,5455	–8,5379
5,6	–1,7481	4,3794	0,2944	–2,3189	1,3266	–9,1268
5,7	–2,1803	5,1346	0,2580	–2,4495	1,1235	–9,7065
5,8	–2,7777	6,2139	0,2195	–2,5838	0,9302	–10,283
5,9	–3,6679	7,8727	0,1790	–2,7219	0,7421	–10,861
6,0	–5,1594	10,727	0,1361	–2,8639	0,5551	–11,444
6,1	–8,2336	16,739	0,0907	–3,0102	0,3656	–12,037
6,2	–18,590	37,308	0,0424	–3,1609	0,1700	–12,643
2π=6.28	–∞	+∞		–3,2899		–13,159

 

 

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к расчетно-графической работе

Расчет рамно-балочных систем

На устойчивость

 

 

Составители: Шакирзянов Рашит Аглеевич,

Шакирзянов Фарид Рашитович

 

Редактор: Г.А. Рябенкова

 

Редакционно-издательский отдел

Казанского государственного архитектурно-строительного университета

 

Подписано в печать 28.04.11 Формат 60´84/16

Заказ № 215 Бумага офсетная № 1 Усл.-печ. л. 1,0

Тираж 200 экз. Печать ризографическая Уч.-изд. л. 1,25

 

Печатно-множительный отдел КГАСУ

420043, г. Казань, ул. Зеленая, 1

 

Поделиться:

Воспользуйтесь поиском по сайту: