 |
Определение переходной функции цепи h(t) .
|
|
|
|
Курсовая работа
Выполнил:
Студент 2 курса, Лукашов А.С.
Группы 114 - З
Проверил:
Ефименко А.А.
Знаменск 2012
Цель работы:
Курсовая работа по дисциплине “Теоретические основы электротехники” имеет целью закрепление знаний студентов по соответствующим разделам учебной дисциплины. В ходе самостоятельного выполнения КР студенты приобретают практические навыки анализы и расчета электрических цепей переменного синусоидального тока в установившихся режимах, построения частотных характеристик, а также анализа цепей при переходных режимах.
1. Дана схема:
Изобразим на схеме токи.
рис 1.1
Данные цепи:
L = 2 мГн
C = 8 мкФ
R1 = 6 Ом
R2 = 200 Ом
R3 = 2 Ом
Um = 115 В
F = 1000 Гц
U0 =15 В
Tимп = 3 τ
Выполнение работы:
Для приложенного входного напряжения uвх(t)=Um * sin(wt)
комплексная амплитуда напряжения: Um= Um * ej0° = 115* ej0°
Рассчитаем индуктивное сопротивление катушки и емкостное сопротивление конденсатора для заданной частоты:
XL = ωL = 2πfL = 2π * 1000 * 2*10-3 = 12,56 Ом
XC = 
= 
= 
= 19,9 Ом
Комплексные сопротивления элементов цепи:
Z1 = R1 = 6 Ом
Z2 = jωL = jXL = j12,56 Ом
Z3 = 
= -jXC = -j19,9 Ом
Z4 = R3 = 2 Ом
Z5 = R2 = 200 Ом
рис 1.2
Zвх = Z1 + Z2 + 
= 6 + j12,56 + 
=
= 6 + j12,56+ 
=
= 6 + j12,56+ 
=
= 6 + j12,56 + 
= (9,88-j6,75) Ом
По закону Ома находим комплексную амплитуду тока в первой ветви:
Im1 = 
= 
= 
= 
= 
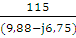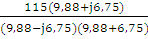= = (7,93+j5,42) А
Показательная форма: Im1 =9,6* ej34,4°А
Токи второй и третьей ветвей найдем по формуле “Разброса токов”:
Im2 = Im1s w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/><w:lang w:val="EN-US"/></w:rPr><m:t>4</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
= 9,6* ej34,4° 
= (0,346-j0,7)А
|
|
|
Im3 = Im1 
= 9,6* ej34,4°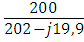 
= (7,62+j6,15)А
В показательной форме: Im2 =0,78* e-j63,7°А
Im3 =9,79* ej38,9°А
Мгновенные значения токов:
i1(t) = 9,6sin(ωt + 34,4°) A
i2(t) =0,78sin(ωt – 63,7°) A
i3(t) = 9,79sin(ωt +38,9°) A
Действующие значения токов (I = 
)
I1 = 6,8А, I2 = 0,55А, I3 = 6,9А,
Комплексную амплитуду выходного напряжения найдем по закону Ома:
Um.вых = Im3·Z4 = 9,79* ej38,9° *2 = 19,58* e-j38,9°A
Мгновенное значение: uвых(t) = 19,58*sin (ωt +38,9°)В
Действующее значение: U = 13,9В
Для построения топографической диаграммы рассчитаем комплексные потенциалы всех точек цепи. При этом потенциал точки е примем равным нулю, иначе говоря, заземлим эту точку. Тогда
φe = 0 В,
φa = Um = 115 В,
φb = φa – Z1Im1 = 115 – 6(7,93+j5,42) = (67,42- j32,52) В
φc = φb – Z2Im1 = (67,42-j32,52) - j12,56 (7,93+j5,42) = (135,5 - j132,1) В
φd = φc – Z3Im3 = (135,5 - j132,1) + j19,9 (7,58+j6,13) = (13,6 + j18,7) В
Для построения топографической и векторной диаграммы на комплексной плоскости, выбрав удобный масштаб(обязательно одинаковый по действительной и мнимой осям), отложим в виде точек найденные комплексные значения потенциалов φa ….φе.Затем соединим точки так, чтобы получить разности соответствующих потенциалов,или векторы,изображающие напряжения на каждом элементе цепи, а именно a-e, a-b, b-c, c-d, d-e, причем стрелку ставим в сторону первой буквы каждой пары, результат построения диаграммы – на рисунке 1.3
Для определения комплексной передаточной функции цепи
W(
) = 
Необходимо выразить выходное напряжение через входное, иначе говоря, проделать практически те же действия, что и при расчете в п.3.2, но только в общем виде:
Zвх = Z1 + Z2 + 
;
Im1 = = 
;
Im3 = Im1 = 
. 
= 
,
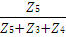Uвых = Im3Z4 = 
Таким образом
W() = 
Подставляем соответствующие выражения для комплексных сопротивлений, получаем
W() =
После домножения на 
и с учетом того, что j2 = -1, окончательно получаем выражение комплексной передаточной функции:
|
|
|
W() =
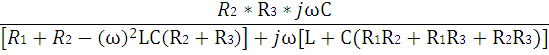
Амплитудно-частотная характеристика (АЧХ) – это зависимость от частоты отношения амплитуд выходного и входного напряжений, или модуль комплексной частотной характеристики:
A(
) = = | W() |,
A() =
По этой формуле строим график. На этом графике фактически построена зависимость от частоты f, выраженной в герцах, с учетом связи с угловой частотой: 
= 2πf
При построении логарифмической амплитудно-частотной характеристики (ЛАЧХ) по оси ординат откладывают значения частоты в логарифмическом масштабе, а по оси ординат – величину 20lg(A()), измеряемую в децибелах.
График ЛАЧХ представлен на рис 1.5
Фазо-частотная характеристика (ФЧХ) – это зависимость от частоты разности фаз между выходным и входным напряжениями, или аргумент комплексной частотной характеристики:
Δψ() = ψUвых – ψUвх = arg(W()),
Δψ() = -arctg(
)
График ФЧХ обычно изображают при логарифмическом масштабе оси частот. Соответствующая кривая приведена на рис 1.6
Определение переходной функции цепи h(t).
Переходной функцией цепи называется реакция на воздействие в виде единичной ступенчатой функции. Значит, для её определения необходимо проанализировать переходной процесс Uвых(t) при подключении цепи к источнику постоянной Э.Д.С.,равной 1В, при нулевых начальных условиях, рис.
рис 1.7
Классический метод.
Классический метод предполагает представление искомой величины (в данном случае выходного напряжения) в виде суммы принужденной, или установившейся, составляющей и свободной составляющей:
uвых(t) = uпр(t) + uсв(t).
1)Расчет принужденной составляющей
В установившемся режиме постоянная э.д.с. может вызывать только постоянные токи в цепи. Постоянный ток через емкость протекать не будет, а индуктивность представляет собой для постоянного тока короткое замыкание. Поэтому ток третьей ветви равен нулю, i3пр = 0, а i1пр = i2пр.
i1пр = i2пр = 
= 
= 0,00485 A
Из уравнения –i2прR2 + i3прR3 + uвыхпр = 0 следует, что
uвыхпр = i2пр R2 = 0,00485*200= 0,97 В
2) Определение общего вида свободной составляющей.
Составляем характеристическое уравнение цепи с помощью приравнивания к нулю выражения для входного сопротивления Z(p) относительно входных зажимов, имея в виду, что сопротивление индуктивного элемента равно pL, а емкостного равно 1/pC.
|
|
|
Z(p) = R1+ pL + 
=0,
p2LC(R2+R3) + p[L+C(R1R2+R1R3+R2R3)] +R1+R2 = 0
С численными значениями:
p23,23*10-6+p 0,0133+206= 0
Корни характеристического уравнения:
p1,2 = 
= (-2059±j5762,5)1/c
Корни характеристического уравнения получились комплексно – сопряженными, что говорит о том, что переходный процесс является колебательным, и свободная составляющая имеет следующий общий вид:
uвыхсв(t) = Ae-δt sin(ωt+γ)
где δ = -2059 1/c – постоянная затухания, ω = 5762,5 рад/с – угловая частота затухания колебаний, А и γ – постоянные интегрирования, которые должны быть определены из начальных условий.
Общий вид результата как суммы двух составляющих:
uвых(t) = uвыхсв + Ae-δt sin(ωt+γ)
3) Определение начальных условий.
Для вычисления постоянных интегрирования необходимо знать начальное значение искомой величины и начальное значение ее первой производной.
Так как выходное напряжение является напряжением на емкости, то по закону коммутации оно не может измениться мгновенно. До подключения э.д.с. оно было равно нулю, следовательно, и в первый момент после подключения остается равным нулю: uвых(0) = 0.
Также по закону коммутации не может измениться мгновенно ток, протекающий по индуктивности, который до подключения тоже был равен нулю. Следовательно i1(0) = 0.
Если обе эти величины равны нулю, то в соответствии с законами Кирхгоффа в момент t = 0 оказываются равными нули и токи второй и третьей ветвей (i2(0) = 0 и i3(0) =0). Но ток i3 – это ток, протекающий через емкость, а он связан с напряжением соотношением i3 = C 
. Значит, значение первой производной выходного напряжения равно току номер 3, деленному на С:
u’вых(0) = 
= 0
4) Вычисляем постоянные интегрирования.
При t = 0:
Из второго уравнения можно найти γ:
γ = arctg (
) = arctg(
) = 70,3°
Из первого уравнения найдем A:
A = - 
= - 
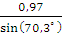= -1,03
Окончательный результат:
h(t) = uвых(t) = 0,97 – 1,03e-2059tsin(5745t+70,3°) В
Постоянная времени процесса
τ = 1/ 
= 1/2059 = 0,485 мС
Операторный метод.
Действия операторным методом при нулевых начальных условиях в значительной мере подобны действиям, при анализе символическим методом цепей синусоидального тока при замене в выражениях сопротивлений комбинации “j 
” на букву “p”. Поэтому можем воспользоваться полученным выражением для комплексной частотной характеристики, записав на месте “j ” букву “p”. Таким образом, мы найдем то, что называется передаточной функцией цепи:
|
|
|
W(
) =
= 
С помощью этой функции легко записать операторное выходное напряжение при заданном операторном входном напряжении:
Uвых(pв) = W(p) Uвх(p)
В нашем случае на входе действует постоянная э.д.с., равная 1В. Ее операторным изображением является 1/p. Значит, операторным изображением переходной функции h(t) будет.
H(p) = 
= 
Остается найти оригинал по формуле разложения:
h(t) = 
e pkt, где
N(p) = R2, M(p) = p[p2LC(R2+R3) + p[L+C(R1R2+R1R3+R2R3)]+R1R2]
Pk – корни многочлена M(p), m – степень многочлена M(p).
Находим корни p(p23,23*10-6 + p0,0133+ 206) = 0
Так как выражение в скобках в точности совпадает с характеристическим уравнением, которое решали классическим методом, то к ранее определенным корням следует добавить еще нулевой корень:
P1 = -2059+j5745, p2 = -2059-j5745, p3 = 0
N(p) не зависит от р, поэтому N(p1) = N(p2) = N(p3) = R2 = 200
M’(p) = 9,69*10-6p2+0,0266p+206
M’(p1) = M’(-2059+j5745) =
= 9,69*10-6(-2059+j5745) 2 +0,0266(-2059+j5745)+206=
=-365,6-j131,1
M’(p2) = M’(-2059-j5745) = -365,6+ j131,1
M’(p3) = M’(0) = 206
= 
= 0,515·ej160,3°
= 0,515· e-j160,3°
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
= 
= 0,97
Подставляем в формулу разложения:
h(t) = 0,515·e j160,3 ·e(−2059+ j5745)t + 0,515e− j160,3e(−2059− j5745)t + 0,97 =
= 0,515·e−2059t (e j(5745t+160,3) + e− j(5745t+160,3)) + 0,97 =
= 1,03e−2059t cos(5745t +160,3°) + 0,97= 0,97 −1,03e−2059t sin(5745t + 70,3°)
Последнее в точности соответствует результату, полученному классическим методом. График переходной функции приведен на рис 1.8
При выполнении последнего пункта задания следует иметь в виду, что зная переходную функцию цепи h(t), нетрудно записать выражение для реакции на любое заданное воздействие с помощью интеграла Дюамеля:
uвых(t) = Uo * h(t) + 
τ)*h(t - τ)dτ
Результатом применения интеграла Дюамеля к воздействию в форме прямоугольного импульса длительностью Тимп и высотой Uо, будет:
uвых(t) = 
Конкретно при заданных U0 = 10 В, Тимп = 3τ = 3*0,263*10-3 и определенной в переходной функции,графики входного и выходного напряжений приведены на рис 1.9
|
|
|
