Комплексная задача оптимизации.

Задача оптимизации планирования в масштабе региона требует рассмотрения достаточно большого числа вариантов различных водоохранных мероприятий при комплексном рассмотрении всех имеющихся источников загрязнения. Объем, возникающий при этой задаче таков, что перебор всех вариантов при наличии большого числа источников затруднен. Поэтому для решения поставленной задачи оптимизации необходим эффективный метод оценки вариантов. Естественным подходом при этом является выделение иерархической структуры во множестве вариантов таким образом, чтобы перебор, отсев и сужение круга поиска начинались на верхнем агрегированном уровне с последующей детализацией и уточнением на нижних уровнях. Соответственно и задачу оптимизации можно разбить на несколько последовательных подзадач. Сначала проводится оптимизация первого (агрегированного) уровня при самом обобщенном описании объекта и грубый отбор лучших вариантов.

На последующих этапах делается детальное сравнение отобранных вариантов и т.д.

Для задач водоохраны может быть рассмотрено 3 уровня оптимизации и соответственно 3 класса моделей:

1. Модели оптимизации функционально-различных технических средств.

2. Модели, в которых рассматривается взаимодействие технических средств одного вида, но разных типов.

3. Модели оптимизации операционно различных технических решений.

Модели первого класса определяют как оптимальным образом распределить «нагрузку» по охране вод между различными группами мероприятий:

1. Мероприятия в рамках самого производства, т.е. замена одного технологического процесса другим, дающим меньше отходов и максимальное повторное использование и т.д., т.е. реализации или достижения наилучших достижимых технологий.
2. Мероприятия по очистке сточных вод до их поступления в водную среду на локальных и внеплощадочных очистных сооружениях.
3. Мероприятия, связанные с самой водной средой (интенсификация процессов самоочищения засчет аэрации и других способов).

Модели второго и третьего классов направлены на дальнейшую детализацию (выбор наилучшего размещения очистных сооружений, степени очистки на каждом сооружении отдельно и т.д.).

В качестве типовых можно назвать следующие задачи оптимизации:

1. Оптимизация степени очистки сточных вод.

2. Выбор оптимальной технологии очистки.

3. Агрегирование очистных мероприятий.

4. Оптимизация водного режима.

5. Оптимизация режима сброса сточных вод.

6. Искусственная аэрация.

7. Надежность функционирования сети станций.

8. Оптимизация очередности строительства.

Рассмотрим более подробно задачи оптимизации первого типа.

Рассмотрим формальную постановку задачи оптимизации степени очистки сточных вод.

Пусть вдоль водотока расположено “n” источников загрязнения. Требуется взаимоувязать степени очистки P_i так, чтобы суммарная стоимость очистных мероприятий была минимальной, т.е. решается задача такого типа:

∑S^or_i(P_i)→min _Pi (13)

∑U^or_i(P_i)≥U^or (14)

P_i^min≤P_i<P_i^max

S^or_i – приведенные затраты на очистку в i-том пункте.

U^or – отнесенное к контрольному створу снижение концентрации примесей в водном объекте, предусмотренное в результате очистки сточных вод.

U^or_i - снижение концентрации примесей в контрольном створе в результате удаления части примеси на i-той очистной станции.

P_i^min и P_i^max – это минимально допустимая и максимально возможная степени очистки сточных вод.

В отдельных работах проводится более детальная постановка задачи для неконсервативных загрязнений, включающих в рассмотрение процессы смешения и самоочищения. Для различного типа задач могут накладываться ограничения по двум и более параметрам. Например, по БПК и растворенному кислороду.

В том случае, если рассматривается большое число точек загрязнения, то применяется разбиение водотока на отдельные участки, содержащие, как правило, не более 10 точек каждый.

Задача выбора оптимальных технологий очистки.

Пусть в некоторой фиксированной точке требуется очищать некоторое количество сточных вод определенного химического состава. Требуемое качество сточных вод на выходе очистной системы считается уже определенным исходя из интересов бассейна в целом. С этой целью используются типовые модели конвективно-диффузионного переноса и превращения веществ (КПД и ПВ) или модели типа уравнений Фелпса-Стритера.

(15)

Она расшифровывается как нестационарная двухмерная неоднородная модель для неконсервативных примесей.

(16)

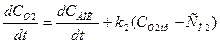(17)

В практике водоохраны имеется много различных видов очистки (механический, химический, биологический и их комбинации).

Для каждого вида и метода очистки считаются известными:

1. степень очистки, допускаемая процессом (т.е. максимально возможная удаляемая доля по каждому компоненту загрязнений).
2. Капитальные и эксплутационные затраты на соответствующие очистные сооружения в зависимости от требуемой мощности очистки.

Задача состоит в том, чтобы спроектировать оптимальную по стоимости (в терминах приведенных затрат) схему очистки, отвечающую заданным требованиям по ПДС для каждого источника загрязнений по всем расчетным компонентам.

В практике проектирования систем водоотведения исследуется зависимость факторов экономической эффективности и качества воды от различия в технологии использования воды и очистки.

Из-за большого разнообразия задач встречаются случаи, когда необходимо определить эффективную компоновку очистки сточных вод при наличии одновременно как органических, так и термических загрязнений.

 

5. Основные характеристики экологического стандарта технологического процесса производства для отдельного вида продукции и нормативы качества окружающей среды. (Технологическое нормирование и нормирование окружающей среды).

Методы прогнозирования

 

 

В настоящее время существует большое количество методик, методов и способов прогнозирования. Однако, все они основаны на двух крайних подходах: эвристическом (основанном на интуитивном, опирающимся на предшествующие опыты решения родственных задач) и математическом (основанном на системе математических соотношений, описывающих изучаемый процесс как явление с помощью любых математических средств, то есть языка дифференциальных или интегральных уравнений, теории множеств, абстрактной алгебры, математической логики, теории вероятности и т.д.).

Наибольший научный интерес представляет собой математический метод прогнозирования. Оно (прогнозирование) заключается в использовании имеющейся информации об объекте прогнозирования, обработки этой информации математическими методами, получении зависимости, связывающей эти характеристики со временем или некоторыми другими независимыми переменными, и вычислении характеристик объекта в заданный момент времени при заданных значениях других независимых переменных. Нахождение закономерностей в поведении прогнозируемого объекта позволяет построить её математическую модель, которая вследствие явления изоморфизма позволяет исследовать реальные физические процессы путём их математического моделирования. Одинаковые по форме математические выражения при различном физическом содержании, входящих в них символов получили название «изоморфные».

Объективная основа всех научных аналогий обуславливается материальным единством мира, единством пространственно-временных форм движения, законов и других общих атрибутов. Математический изоморфизм различных физических систем позволяет с помощью одних систем изучать другие. На выбор математической модели прогнозируемого объекта оказывают влияние цель и задачи прогнозирования, а также величина интервала прогнозирования. С применением методов и средств обратных (определение граничных условий по заданному физическому полю) и инверсных (определение коэффициентов модели по заданному физическому полю) задач определяются неизвестные параметры математической модели объекта. Прогнозирующая система должна быть замкнутой по отношению к результатам прогнозирования, что дает возможность внесения поправок и изменений в элементы прогнозирующей системы. Модель должна строиться для решения конкретной задачи исследования и отражать те стороны и связи изучаемого явления, которые являются важными именно для данного исследования. В инженерных исследованиях выделяют следующие типы моделей:

1. Модели детерминированных процессов при полной априорной (до начала исследования) информации об их параметрах;

2. Модели детерминированных при неполной априорной информации о параметрах модели (неизвестны начальные условия при известных дифференциальных уравнениях; неизвестны некоторые коэффициенты);

3. Процесс является детерминированным и информация о нем не искажена, но вид модели процесса априорно не известен.

4. О процессе априорно ничего не известно, и поступающая информация искажена (является искаженной) различными помехами.

 

В настоящее время наиболее разработаны методы и средства для первых 2-х типов моделей. Анализ результатов математического прогнозирования позволяет принимать обоснованное решение по комплексу мероприятий, связанных с управлением окружающей среды. Прогнозирование мероприятий по охране вод при сбросе производственных, бытовых и сельскохозяйственных стоков в водоемы связано с необходимостью:

а) определить степень очистки сточных вод;

б) обеспечить стабильность биологических циклов в заданных участках водоемов и водотоков ниже выпуска сточных вод при наименьших затратах, распределенных на очистку между всеми предприятиями, которые сбрасывают сточные воды в пределах заданного участка.

Поэтому при проектировании и строительстве любого природоохранного комплекса (на любой его стадии) необходимы соответствующие его типу и масштабу проектно-изыскательские работы и теоретическое обоснование в виде численного прогноза. В качестве базовых используются экологические стандарты технологического процесса производства и нормативы качества окружающей среды.

 

Табл. Основные характеристики экологических стандартов технологического процесса для отдельного вида продукции и норматива качества окружающей среды

 

Технологическое нормирование – экологический стандарт технологического процесса ЭСТП	Нормирование окружающей среды
Предмет нормирования
Количество вредных веществ, которые могут быть допущены к попаданию в водную среду от данного технологического процесса производства определенного вида продукции вследствие использования апробированного в мировой практике инженерно-технических и технологических решений	Структурные гидрохимические и гидробиологические показатели качества природных вод и донных отложений, а также интегральная оценка токсичности воды.
Количество нормированных показателей
должно быть достаточным для оценки уровня прогрессивности принятого водопользователем технологического процесса, соответствующего с точки зрения загрязнения окружающей среды определению «наилучшей существующей технологии»	должно быть достаточным для того, чтобы отследить процессы происходящие в водном бассейне как по гидрохимическим, так и по гидробиологическим показателям с целью обеспечения устойчивости гидро-экосистемы.
Номенклатура нормированных показателей
Должны использоваться интегральные показатели, характеризующие тенденцию сокращения сброса вредных веществ путем внедрения водопользователем новых прогрессивных технологических процессов с наименьшими потерями в водную среду используемых в технологическом процессе сырья, химикатов, продуктов переработки	1. по гидрохимическому блоку: - общефизические показатели и показатели неорганических веществ; - общие показатели органических веществ; - показатели неорганических промышленных загрязняющих веществ; - показатели органических промышленных загрязняющих веществ; 2. по гидробиологическому блоку: - показатели обилия организмов; - характеристики качественного состава; - пространственно-временное распределение; - биотические взаимодействия; - структура популяций; 3. интегральный показатель токсичности.
Цель установления норматива
Побудить водопользователя к внедрению прогрессивных технологических процессов с минимальным загрязнением окружающей среды, соответствующих определению «наилучшая существующая технология».	Обеспечение устойчивости гидроэкосистемы и сохранение способности ее к саморегуляции за счёт компенсационных механизмов. Оптимальное использование экологической емкости гидроэкосистемы и ее экологического потенциала. Поддержание самоочищающей способности гидроэкосистемы.
Для чего используются нормативы
Для управления качественными характеристиками водного объекта и прогнозирования его состояния. В перспективе нормативы должны использоваться как экономические рычаги государственного регулирования качества водных объектов, реализуемые путем взимания платежей за загрязнение окружающей среды	Для обеспечения заданных стандартов качества поверхностных вод в створах в соответствии с категорией водопользования и поддержания гидроэкосистемы на гомеостатическом плато. Для распределения квот нагрузки между всеми водопользователями и для регулирования сброса загрязняющих веществ с целью эффективного использования биологических, химических и физических процессов самоочищения. Сегодня нормативы используются для осуществления механизмов платежей за загрязнение поверхностных вод.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: