Природа молекулярных колебаний

 

 

 

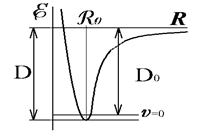
Истинный энерге­тический уровень связывающего со­стояния 2-х атом­ной молекулы не может совпадать непосредственно с минимумом потенциальной кривой

в адиабатическом приближении. Это означало бы на­рушение принципа Гейзенберга  R × p _x ³ h.

Если R º R ₀, то R º0, и это невозможно...!!!

Проблема решается за счёт поднятия истинного уровня над минимумом, и при R = R ₀ возникает необходимый диапазон отклонений  R ¹0. Они периодичны – это колебания. Максимальное отклонение от положения равновесия– амплитуда колебания.

Потенциал молекулярных колебаний. Амплитуда.

Около минимума вблизи R ₀ адиабатический потенциал – энергетическую кривую можно ап­проксими­ровать параболой. Периодически меняющееся смещение равно x = R - R ₀. Движение ядер с параболическим по­тенциалом – гармоническое колебание. Его законы, полученные в классической физике, в основном справед­ливы и в квантовой механике. Спра­ведливы известные соотношения. Потенциальная энергия и силовая кон­станта равны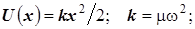  

Формула квантования энергии осциллятора: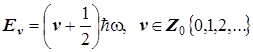  

Возбуждение молекулярных колебаний при поглощении излучения.

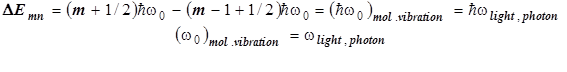
Так, регистрируя резонансную частоту поглощаемого излучения, тем самым изме­ряем и собственную частоту молекулярного колебания.

Валентные колебания (периодические смещения ядер от равновесия):

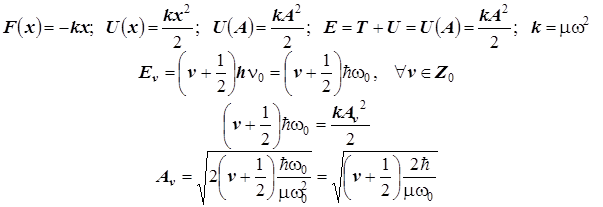
Здесь представлены величины:

Колеблющаяся масса связи A - B рассчитывается как приведённая величина:

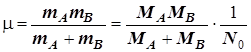
N ₀ -число Авогадро, M_A, M_B – молекулярные массы в у.е.,

_2 =2c(1/) - Круговая частота колебания.

Последняя формула позволяет вычислить амплитуду колебания на основании его соб­ственной частоты. Линейное колебание это простейший вид молекулярной деформации.

Если оно состоит лишь в удлинении и сокращении связи, то называется ва­лентным. Амплитуда вычисляется на основании лишь собственной частоты и даёт возможность количе­ственно и наглядно оценить степень деформируемости молекулы.

ПРИМЕРЫ Вы найдёте в кафедральном практикуме-СБОРНИКЕ Методические указания к лабораторным работам по курсу “Физическая химия” 1985 год. “колебательная спектроскопия”, 4.5.2.Стр. 41-44, а также в новом практикуме 2002 года издания

Задача 2.

 

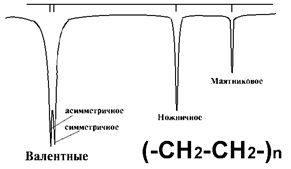
В спектре ИК-поглощения полиэтилена (-CH₂-CH₂-)₂ наблюдается сравнительно небольшое число хорошо выделенных колебательных полос. Это полосы с частотами (волновыми числами) (720, 1420, 2800, 2900) см^-1. Две пер­вые полосы принадлежат деформационным колебаниям (маятниковому и нож­ничному). Полосы 2800, 2900 см^-1 принадлежат валентным колебаниям. Рассчи­тать амплитуды валентных колебаний на двух низших уровнях (v =0, 1).

 

 

 

Рис. ИК-спектр Полиэтилена (тонкая плёнка)

 

РЕШЕНИЕ. Удобно выполнить в системе СГС. (Вы можете сделать это и в системе СИ).

В обоих этих колебаниях колеблющаяся масса одна и та же. Это приведённая

1) Приведённая масса связи C-H равна _CH = [(12×1)/ (12+1)] / 6.023×10²³ г =1.533×10 ^-24 г

2) В обоих валентных колебаниях (симметричном 2860 и асимметричном 2950) синхронно движутся ядра двух атомов водорода, поэтому колеблющаяся масса удваивается и равна 2×1.533×10 ^-24 г» 3.07×10 ^-24 г

3) Круговая частота колебания равна _2 ×c× (1/)=6.28×3×10¹⁰×2850 =5.369×10¹⁴ рад/с

4) Величина 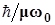 = (6.62×10^-27/2)/ (3.07×10 ^-24×5.369×10¹⁴)= 0.64×10^-18 см²

5) Амплитуда нулевого колебательного уровня:

A₀=(0.64×10^-18 см ²)^1/2 » 0.8×10^-9 см =0.08 A⁰

6) Это значение примерно на порядок менее длины связи.

7) Амплитуда первого колебательного уровня:

A₀=(3×0.64×10^-18 см ²)^1/2 » 1.39×10^-9 см» 0.14 A⁰

Амплитуда возрастает на возбуждённых уровнях....

ВЫВОД

 

Известно, что длина химической связи C-H в соединениях равна 1.06 - 1.1 A⁰.

Найденные амплитуды имеют разумные физические значения, составляя в основном и близлежащем возбуждённом состояниях 8-14% от длины связи.

Деформационные колебания (периодические изменения валентных углов): (эти вычисления Вы выполняете по мере возможности)

Периодические изменении валентных углов называются деформационными колеба­ниями. В этом случае амплитуда уже не линейная, а угловая.

Воспользуемся известными аналогиями в описании поступательного и вращательного движений. При переходе от линейного к вращательному движению следует заменить:

линейное смещение x -угловым отклонением .

линейную амплитуду A - угловой амплитудой .

массу  - моментом инерции I.

Константа упругости линейного колебания k =^заменяется аналогичной константой упругости углового (деформационного) колебания  =I^

Формула для расчёта линейной амплитуды превратится в формулу для вычисления угловой амплитуды.

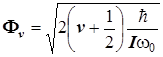
Задача 2.

 

В спектре ИК-поглощения полиэтилена (-CH₂-CH₂-)₂ наблюдается сравнительно небольшое число хорошо выделенных колебательных полос. Это полосы с частотами (волновыми числами) (720, 1420, 2800, 2900) см^-1. Две пер­вые полосы принадлежат деформационным колебаниям (маятниковому и нож­ничному). Две последние полосы принадлежат валентным колебаниям. Рассчи­тать амплитуды деформационных колебаний на основных уровнях (v =0).

Пример расчёта смотри в практикуме

“Методические указания к лабораторным работам по курсу “Физическая химия””

1985 год. “колебательная спектроскопия”, 4.5.2.Стр. 41-44.

Указание. В этой задаче главный упор делается на вычисление моментов инерции. У маят­никового колебания он равен удвоенному моменту инерции связи C-H. У ножничного равен половине момента инерции связи C-H.

Повороты отдельных связей принимаются относительно атома C.

123	Поделиться:

Воспользуйтесь поиском по сайту: