Найти точки пересечения прямой общего положения с поверхностью

(задачи 8,9,10)

План:

1. Заключить прямую во вспомогательную плоскость;

2. Построить линию пересечения этой плоскости с поверхностью;

3. Точки, которые являются общими для полученной линии пересечения и исходной прямой, - искомые;

4. Определяется видимость.

Задача №8

Найти точки пересечения наклонной призмы с прямой (рис.28).

1.

Р2

Заключим прямую во фронтально-проецирующую плоскость

lÎP^П_2.

2. Поскольку фронтальная проекция Р₂ плоскости Р, в которую заключена прямая l, совпадает с её фронтальной проекцией l₂, то фронтальные проекции точек пересечения ребер призмы

А₁А₂¢Çl₂=1₂; B₁B₂¢Çl₂=2₂; C₁C₂¢Çl₂=3₂

определяются в их пересечении с фронтальным следом плоскости Р₂.

Горизонтальная проекция сечения 1₁2₁3₁ находится с помощью линии

Рис. 28

связи.

 

3. Пересечением 1₁2₁3₁ с горизонтальной проекцией прямой l₁ отмечаются точки М₁ и N₁ - горизонтальные проекции точки пересечения прямой с призмой, затем строятся их фронтальные проекции M₂, N₂.

4. Определяют видимость.

Проекция точки (×)M₁ лежит на видимой части сечения ® М₁ - видима, проекция l₁ до М₁ - видима, между М₁ и N₁ - невидимы. Проекция N₁ лежит на невидимой части сечения ® N₁ - невидима и l₁ до ребра С₁С₁¢ - невидима.

 

Рассмотрим видимость точек на плоскости П₂.

Так как грань А₂А₂¢В₂В₂¢ видима ® (×) М₂, принадлежащая этой грани - видима. Грань А₂А₂¢С₂С₂¢ - невидима ® (×)N₂ - принадлежащая этой грани - невидима. l₂ - до М₂ - видима, между М₂ и N₂ - невидима, от N₂ - С₂С₂¢ - невидима.

 

 

Задача №9

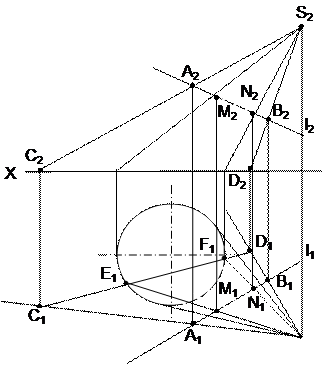Определить точки пересечения прямой с конусом

(рис.29)

 

 

Рис.29

Заключить прямую в плоскость, проходящую через вершину конуса. Для этого соединим две произвольные точки прямой А и В с вершиной S (рис.29).

Найти линию сечения её с плоскостью основания конуса (точки С и D), тогда в точках Е и F пересечения прямой CD с окружностью основания конуса начнутся образующие SE и SF, по которым вспомогательная плоскость рассечет поверхность. Пересечение прямой АВ в точках М и N с образующими SE и SF определяет точки пересечения прямой с поверхностью конуса.

Задача №10

Найти точки пересечения со сферой (рис.30).

Заключим прямую l во фронтально проецирующую плоскость: lÌQ^П₂. В сечении сферы этой плоскостью получится окружность, которая на плоскость П₂ проецируется в отрезок 1₂8₂, а на плоскость П₁ в эллипс.

Для определения точек, принадлежащих этому эллипсу, сфера и вспомогательная плоскость Q рассекаются горизонтальными плоскостями - посредниками (a, b). Чем больше таких плоскостей, тем точнее будут построения. Проводить их следует на участке между наивысшей (1) и наинизшей (8) точками, лежащими на главном меридиане. Эти точки называются опорными. К опорным также относятся точки 4 и 5, лежащие на экваторе.

Каждая из плоскостей - посредников рассекает сферу по окружности соответствующего радиуса r_a, r_b. Эти окружности на плоскость П₁ проецируются в окружности. Горизонтальные проекции точек линии сечения (1₁, 2₁, 3_1, ..., 8₁) лежат на окружностях соответствующих радиусов.

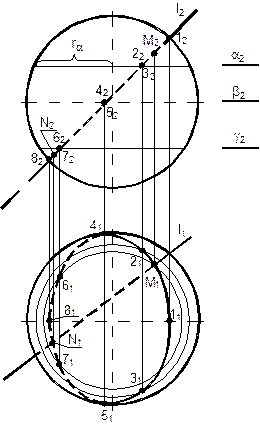
P2 Рис.30

Соединяем их с учетом видимости. Проекция прямой l1 пересекает сечение в точках М1 и N1. Точки M и N – искомые. Последний этап – определение видимости. На горизонтальной проекции видны те точки (11; 21; 31; 41; 51), фронтальная проекция которых расположена выше экватора, а проекции точек 61, 71, 81 - невидимы.M1 - видима, N1 - невидима. На фронтальной проекции видны те точки, горизонтальная проекция которых расположена ниже главного меридиана: N2 - видима, M2 - невидима. Между точками пересечения прямая всегда невидима.

 

Задача №11

Найти линию пересечения плоскости общего положения с пирамидой (рис.31).

План:

1. На поверхности выделить простейший линейчатый каркас;

2. Для каждой линии каркаса найти точки пересечения их с плоскостью (см. задачу №3);

3. Полученные точки соединить с учетом видимости.

Если поверхность гранная (пирамида, призма), то задача на определение линии пересечения сводится к нахождению точки пересечения ребер поверхности с секущей плоскостью. Например, найдем точку пересечения ребра SA с плоскостью a(m||n).

 

SAÌP^П₂ ; aÇP=1,2 (1₂,2₂®1₁,2₁); ASÇ12=M(M₁,M₂).

Аналогично находим точки пересечения ребер:

SBÇa=N(N₁®N₂)

SCÇa=L(L₁®L₂)

Соединить точки с учетом видимости ®DMLN.

 

 

 

 

Рис. 31

 

 

Пересечение поверхностей

Для построения линии пересечения поверхностей следует использовать вспомогательные плоскости, как правило, плоскости уровня, которые рассекают исходные поверхности по простейшим сечениям (окружности, прямые линии). Общие точки этих сечений, принадлежат линии пересечения поверхностей. Набирая достаточное количество точек, соединяют их с учетом видимости. Характерными точками сечения являются низшая и высшая точки сечения, точки смены видимости.

Задача №12

Найти линию пересечения прямого кругового конуса со сферой (рис. 32).

 

Для получения опорных (низшей и высшей) точек сечения рассекаем поверхности фронтальной плоскостью уровня l (l₁), проходящей через ось конуса и центр сферы. В этом случае фронтальные проекции конуса и сферы являются также фронтальными проекциями сечения конуса и сферы. Точки 1₂ и 2₂ - точки пересечения указанных сечений – фронтальные проекции искомых точек.

 

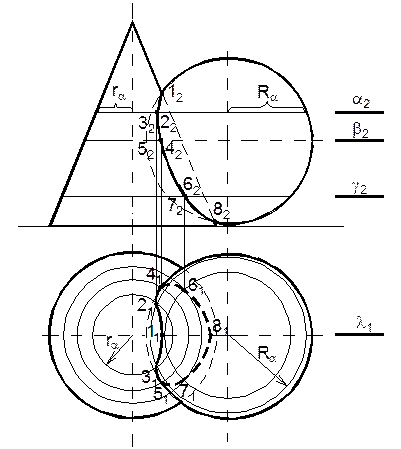
Рис. 32

Для построения остальных точек сечения используют горизонтальные плоскости - посредники a, g, b, причем через горизонтальную ось сферы проведение секущей плоскости обязательно.

Так, в частности, в результате пересечения поверхностей горизонтальной плоскостью a (a₂) в сечении получаем окружности радиусом R_a и r_a, которые пересекаются на плоскости П₁ в точках 3₁ и 4₁, фронтальные проекции 3₂, 4₂ которых лежат на проекции плоскости a (a₂).

Определение видимости точек сечения.

Точки, принадлежащие линии сечения поверхностей видны, если они видны одновременно на двух поверхностях.

На горизонтальной проекции конуса все точки видимы. На горизонтальной проекции сферы видны те точки, которые на фронтальной проекции сферы лежат в верхнем полушарии сферы. Для получения точек смены видимости (5,6) рассекаем поверхности, плоскостью b (b₂), проходящей через экватор сферы, получаем проекции 5₁6₁®5₂6₂; проекции точек 1₁, 3₁, 4₁, 5₁, 6₁ - видимы, проекции точек 7₁, 8₁, 9₁, 10₁ - невидимы. Для получения линии сечения соединяем их с учетом видимости.

 

Задачу №13 на построение линии пересечения поверхностей решить аналогичным методом самостоятельно. В качестве секущих плоскостей рекомендуется использовать фронтальные плоскости - посредники.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: