 |
Последовательность выполнения работы
|
|
|
|
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ
Теоретические сведения
Абсолютная и относительная погрешности. Знак равенства в приближенных вычислениях имеет не тот смысл, как в алгебре. Равенство означает не совпадение значений, а лишь близость значений. Точность приближенного равенства, т.е. степень близости точного значения 
и приближенного 
, характеризует абсолютная погрешность, 
.
На практике вместо абсолютной погрешности, которая обычно неизвестна, используют предельную абсолютную погрешность, 
причем слово предельная для краткости опускают. Если интересует точность уже проведенного расчета, то за берут число, которое возможно ближе к “истинной” погрешности. Называют это оценкой погрешности. Оценка погрешности может быть грубой или более точной. Погрешность может быть задана заранее, тогда вычисление проводится так, чтобы это неравенство выполнялось.
Для того чтобы записать, что является приближенным значением с абсолютной погрешностью , пишут:
Относительной погрешностью, часто выражаемой в процентах, называют величину 
такую, что
Относительная погрешность более полно характеризует степень точности приближенного числа, поскольку можно сравнивать точность задания величин, как существенно различающихся по порядку, так и выраженных в разных единицах измерения.
Верные и сомнительные цифры. Значащую цифру называют верной в узком смысле, если абсолютная погрешность числа не превышает 1/2 единицы разряда, соответствующего этой цифре.
Например, 
; 
;
.
Имеем 
; также 
. Следовательно, верные цифры в узком смысле 9 и 3. Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превышает единицы разряда, соответствующего этой цифре (В примере 9, 3 и 4). Цифры, стоящие в более младших разрядах, называют сомнительными.
|
|
|
Последовательность выполнения работы
Пример 1. Заданы точное и приближенное значения числа. Найти абсолютную и относительную погрешности (решение приведено на рис. 2.1)
; 
; 
Рис. 2.1 – Решение примера 1
Пример 2. Найти предельные абсолютные и относительные погрешности чисел 
и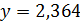 
, если они имеют только верные цифры: а) в узком смысле, б) в широком смысле.
Решение задания приведено на рис. 2.2
Рис. 2.2 – Решение примера 2
Пример 3. Задано число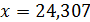 
и относительная погрешность 
. Определить количество верных цифр числа по его относительной погрешности.
Решение: так как 
и 
, то число 
имеет, по крайней мере, две цифры, верных в узком смысле. Определим абсолютную погрешность:
Значит, в узком смысле верными являются цифры 2 и 3.
Пример 4. Пусть , 
. Определить количество верных цифр в числе .
Решение: так как и 
, то число имеет, по крайней мере, одну цифру, верную в узком смысле (цифра 9). Проверим этот результат, используя определение цифры, верной в узком смысле.
Для этого определим абсолютную погрешность:
Полученная абсолютная погрешность не превышает половину единицы разряда сотен. Следовательно, цифра 9 верна в узком смысле, как по относительной погрешности, так и по абсолютной.
Пример 5. Пусть ,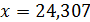 
. Определить все верные цифры числа.
Решение: так как 
, то число имеет, по крайней мере, четыре цифры, верных в узком смысле (цифры 2, 4, 3, 0). Вычислим
Пример 6. При взвешивании двух грузов получили следующие значения их масс 
кг и 
кг. Считая абсолютную погрешность взвешивания равной 1 г, определить относительную погрешность измерения масс тел 
. Какое из тел взвешено более точно?
Решение примера на рис. 2.3.
Рис. 2.3 – Решение примера 6
Пример 7. Определить, какое равенство точнее 
или 
Решение: найдем значения данных выражений с бóльшим числом десятичных знаков: 
, 
. Вычислим предельные абсолютные погрешности, округляя их с избытком:
|
|
|
Предельные относительные погрешности составляют:
Так как 
, то равенство 
является более точным.
Пример 8. Округлить сомнительные цифры числа, оставив верные знаки:
а) в узком смысле 
;
б) в широком смысле 
.
Определить абсолютную погрешность результата.
Решение:
а) пусть 
. Согласно условию, погрешность 
; это означает, что в числе 
верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдём приближенное значение числа, сохранив десятые доли:
Полученная погрешность больше 0,05; значит, нужно уменьшить число цифр в приближенном числе до двух:
Поэтому обе оставшиеся цифры верны в узком смысле.
б) 
; 
тогда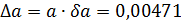 
. В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:
Значит, и в округлённом числе 
все три цифры верны в широком смысле.
Пример 9. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры:
а) в узком смысле 
;
б) в широком смысле 
Решение: а) так как все четыре цифры 
верны в узком смысле, то абсолютная погрешность 
, а относительная погрешность
б) так как все пять цифр числа 
верны в широком смысле, то: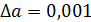 
;
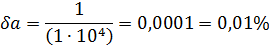
da=1/(1∙104)=0,0001= 0,01%.
Пример 10. Вычислить и определить погрешности результата.
где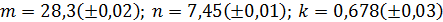 
Решение. Находим 
Далее имеем
откуда 
4. Контрольные вопросы:
1. Что такое абсолютная и относительная погрешности?
2. Что значит цифра, верная в широком и узком смыслах?
3. Как определить количество верных цифр по относительной погрешности приближенного числа?
4. Как определяются абсолютная и относительная погрешности в арифметических действиях?
Варианты заданий к лабораторной работе 2
Задание 1
1) Определить, какое равенство точнее.
2) Округлить сомнительные цифры числа, оставив верные знаки:
а) в узком смысле; б) в широком смысле.
Определить абсолютную погрешность результата.
3) Найти предельные абсолютные и относительные погрешности
чисел, если они имеют только верные цифры:
а) в узком смысле; б) в широком смысле.
Варианты заданий приведены в табл. 1.1.
| № вар. | Задание 1 | Задание 2 | Задание 3 | |||
| а) | б) | а) | б) | |||
| 19/41=0,463 |  =6,630
| 22,55300 (±0,01600) | 2,85460; d=0,30% | 0,2387 | 42,8840 | |
| 7,15=0,467 |  =5,480
| 17,28340; d=0,30% | 6,42570 (±0,00240) | 3,7510 | 0,5370 | |
 =3,240
| 4/17=0,253 | 2,34850 (±0,00420) | 0,34484; d=0,40% | 11,4450 | 2,0430 | |
| 15/7=2,14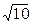0 |  =3,160
| 34,83400; d=0,10% | 0,57480 (±0,00340) | 2,3445 | 0,7450 | |
| 6/7=0,857 |  =2,190
| 5,43500 (±0,00280) | 10,84410; d=0,50% | 8,3450 | 0,2880 | |
| 12/11=1,091 |  =2,610
| 8,24163; d=0,20% | 0,12356 (±0,00036) | 12,4500 | 3,4453 | |
| 2/21=0,095 |  =4,690
| 2,45430 (±0,00320) | 24,56430; d=0,10% | 0,3740 | 4,3480 | |
| 23/15=1,530 |  =3,130
| 23,57400; d=0,20% | 8,34450 (±0,00220) | 20,4300 | 0,5760 | |
| 6/11=0,545 |  =9,110
| 3,78340 (±0,00410) | 7,52100; d=0,12% | 5,6340 | 0,0748 | |
| 17/19=0,895 |  =7,210
| 21,68563; d=0,30% | 13,53700 (±0,00260) | 41,7200 | 0,6780 | |
| 21/29=0,723 | =6,630
| 0,35670; d=0,042% | 13,62530 (±0,00210) | 0,5746 | 236,5800 | |
| 50/19=2,630 |  =5,190
| 1,78400 (±0,00630) | 0,85637; d=0,21% | 18,3570 | 2,1600 | |
| 13/17=0,764 |  =5,560
| 3,68780 (±0,00130) | 15,87300; d=0,42% | 0,3648 | 21,7000 | |
| 7/22=0,318 |  =3,600
| 27,15480 (±0,00160) | 0,39450; d=0,16% | 8,7300 | 14,8620 | |
| 17/11=1,545 |  =4,240
| 0,86470 (±0,00130) | 24,36180; d=0,22% | 2,4516 | 0,8630 | |
| 5/3=1,667 |  =6,160
| 3,75420; d=0,32% | 0,98351 (±0,00042) | 62,7400 | 0,3890 | |
| 49/13=3,770 |  =3,740
| 83,73600; d=0,085% | 5,64830 (±0,00170) | 5,6432 | 0,0085 | |
| 13/7=1,857 |  =2,640
| 2,88670; d=0,43% | 32,74860 (±0,00120) | 0,0384 | 63,7450 | |
| 19/12=1,580 |  =3,460
| 4,88445 (±0,000520) | 0,096835; d=0,32% | 12,6880 | 4,6360 | |
| 51/11=4,640 |  =5,910
| 38,42580 (±0,00140) | 0,66385; d=0,34% | 6,7430 | 0,5430 |
|
|
|
Задание 2
Задание. Вычислить и определить погрешности результата.
Варианты заданий приведены в табл. 1.2
| Вариант | ||
| a | 3,8500 (±0,0001) |
| b | 2,0435 (±0,0004) | |
| c | 62,6000 (±0,0001) | |
| Вариант | ||
| a | 4,300 (±0,050) |
| b | 17,210 (±0,020) | |
| c | 8,200 (±0,050) | |
| m | 12,417 (±0,003) | |
| n | 8,370 (±0,005) | |
| Вариант | ||
 : 
| a | 1,141(±0,002) |
| b | 3,156 (±0,001) | |
| h | 1,140 (±0,030) | |
| Вариант | ||
| a | 228,600 (±0,060) |
| b | 86,400 (±0,020) | |
| c | 68,700 (±0,050) | |
| Вариант | ||
| a | 13,500 (±0,020) |
| b | 3,700 (±0,020) | |
| m | 4,220 (±0,004) | |
| c | 34,500 (±0,020) | |
| d | 23,725 (±0,005) |
| Вариант | ||
| a | 8,530 (±0,050) |
| b | 6,271 (±0,002) | |
| h | 12,480 (±0,002) | |
| Вариант | ||
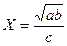
| a | 3,850 (±0,004) |
| b | 16,200 (±0,050) | |
| c | 10,800 (±0,100) | |
| Вариант | ||
| a | 2,754 (±0,001) |
| b | 11,700 (±0,040) | |
| m | 0,560 (±0,005) | |
| c | 10,536 (±0,002) | |
| d | 6,320 (±0,008) | |
| Вариант | ||
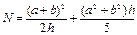
| a | 0,5620 (±0,0010) |
| b | 0,2518 (±0,0025) | |
| h | 0,6800 (±0,0030) | |
| Вариант | ||
| a | 3,4560 (±0,0020) |
| b | 0,6420 (±0,0005) | |
| c | 7,1200 (±0,0040) | |
| Вариант | ||
| a | 23,160 (±0,020) |
| b | 8,230 (±0,005) | |
| c | 145,500 (±0,080) | |
| d | 28,600 (±0,100) | |
| m | 0,280 (±0,006) | |
| Вариант | ||
| a | 8,51 (±0,020) |
| A | 23,42 (±0,005) | |
| S | 45,80 (±0,100) | |
| h | 3,81 (±0,004) | |
| Вариант | ||
| a | 0,6430 (±0,0005) |
| b | 2,1700(±0,0020) | |
| c | 5,8430 (±0,0010) | |
| Вариант | ||
| h | 21,10 (±0,040) |
| a | 22,08 (±0,020) | |
| b | 31,11 (±0,002) | |
| Вариант | ||
| a | 27,160 (±0,006) |
| b | 5,030(±0,010) | |
| c | 3,600 (±0,020) | |
| m | 12,375 (±0,004) | |
| n | 86,200 (±0,050) | |
| Вариант | ||
| a | 0,3575 (±0,0002) |
| b | 2,6300 (±0,0100) | |
| c | 0,8540 (±0,0005) | |
| Вариант | ||
| a | 16,342 (±0,001) |
| b | 2,500 (±0,030) | |
| c | 38,170 (±0,002) | |
| d | 9,140 (±0,005) | |
| m | 3,600 (±0,040) | |
| Вариант | ||
| a | 2,456 (±0,0015) |
| h | 1,760 (±0,0020) | |
| Вариант | ||
| D | 54,000 (±0,500) |
| d | 8,235 (±0,001) | |
| Вариант | ||
| D | 36,500 (±0,100) |
| d | 26,350 (±0,005) |
|
|
|
|
|
|
