Распознавание изображений, содержащих ярко выраженную текстуру.

1 Цель работы: изучить методы распознавания текстур, получить практические навыки распознавания, реализовать алгоритмы распознавания.

 

2. Указания к выполнению лабораторной работы.

 

Текстура является характерным признаком, применяемым для сегментации изображений на области интереса и для классификации этих областей. Текстура описывает пространственное распределение цветов или значений интенсивности на изображении. Одна из задач текстурного анализа заключается в точном определении понятия текстуры. Известны два основных подхода.

Структурный подход. Текстура представляет собой множество примитивных текселов, расположенных в некотором регулярном или повторяющемся порядке. Тогда структурное описание текстуры могло бы состоять из описания текселов и их пространственной взаимосвязи.

Статистический подход. Текстура является количественной характеристикой распределения значений интенсивности в области изображения. Вместо обнаружения текселов по пиксельным данным полутоновых (или цветных) изображений мож­но вычислить численные характеристики текстур (текстурные статистики).

Текстура изображения обычно включает упорядоченные узоры, состоящие из правильных элементов (которые иногда называют текстонами). Естественный способ представления текстуры – это найти текстоны и описать их расположение. Недостаток такого описания текстуры заключается в том, что нет известного канонического набора текстонов, т.е. не ясно, что следует искать. Преимущество такого метода состоит в том, что простые элементы узора нетрудно найти с помощью фильтрации изображения.

Преимущество преобразования изображения в новый базис, которое дает его свертка с фильтром, состоит в том, что этот процесс выявляет структуру изображения. Это происходит благодаря тому, что реакция фильтра сильнее тогда, когда узор изображения на каком-либо участке похож на ядро фильтра, и слабее в противном случае. Таким образом, можно представить текстуру изображения в виде реакции набора фильтров. Набор различных фильтров должен состоять из серий узоров – как правило, пятен и полос – при определенной последовательности масштабов. Несмотря на то, что такой подход является сильно избыточным, он дает представление структуры (ее «пятнистости», «полосатости» и т.д.), которое является очень полезным.

Фильтры пятен очень полезны благодаря сильной реакции на небольшие участки, которые отличаются от соседних, также они могут определять неориентированную структуру. Фильтры полос ориентированы и лучше реагируют на ориентированную структуру. Единственно правильного ответа на вопрос, какими фильтрами стоит пользоваться и сколько должно быть фильтров, нет. Обычно берется, по меньшей мере, один фильтр пятен и набор ориентированных фильтров полос для различных направлений, масштабов и фаз. Фазой полосы называют фазу поперечного сечения перпендикулярно полосе, которую определяют по аналогии с фазой синусоиды. Большое число фильтров приводит к более подробному, но в тоже время и к более перегруженному описанию изображения.

Методы сегментации текстурных изображений делятся условно на две категории: статистические и структурные.

Примером статистического подхода является использование матриц совпадений, формируемых из исходных изображений, с последующим подсчетом различных статистических моментов (характеристик).

Метод матрицы совпадений позволяет определить, содержат ли участки изображения текстуры одного класса путем вычисления для каждого участка так называемой матрицы совпадений.

Матрица совпадений – это двумерный массив P, в котором индексы строк и столбцов образуют множество V допустимых на изображении значений пикселей. Например, для полутоновых изображений V может быть множеством допустимых значений интенсивности (яркости), а для цветных изображений V может быть множеством возможных цветов. Значение P(а, b) указывает, сколько раз значение a встречалось на изображении в некотором заданном пространственном отношении со значением b. Пространственное отношение описывается вектором d. Этот вектор задает смещение между пикселем с яркостью a и пикселем с яркостью b. Например, в качестве пространственного отношения может быть выбрано «значение b является правым соседом для значения a».

Через d обозначим вектор перемещения (dx, dy), где dx соответствует перемещению в направлении строк, a dy – перемещение в направлении столбцов. Следовательно, формально матрицу совпадений можно записать следующим образом:

 

(1)

 

где

 

(2)

. (3)

 

Матрицы совпадений представляют свойства текстуры, но они не удобны для непосредственного применения при анализе изображений, например, для сравнения двух текстур. Вместо этого матрицы совпадений используются для вычисления числовых характерных признаков, которые могут служить более компактным представлением текстуры. На основе матрицы совпадений можно вычислить следующие характерные признаки:

 

;

;

;

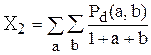; (4)

;

;

.

 

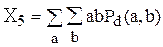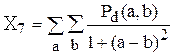Сегментация изображения на основе матриц совпадений проводится следующим образом. Входное изображение размерностью N×N разбивается на фрагменты размером n×n. В результате получаем × фрагментов.

Для каждого фрагмента строятся четыре матрицы для следующих векторов перемещения:

 

d₁=(0, 1), d₂=(0, -1), d₃=(-1, 0), d₄=(1, 0). (5)

 

По полученным матрицам вычисляют характеристики (4). В результате для каждого фрагмента получают вектор характеристик , состоящий из 28 элементов. Полученный вектор нормализуют путем деления на максимальное значение.

Те фрагменты, для которых выполняется условие (6), принадлежат одному классу текстур.

 

(6)

 

где ρ – мера близости;

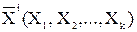– вектор признаков i-ого фрагмента;

i,j=1,…, , i≠j;

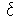– некоторая пороговая величина.

Если вектора фрагментов удовлетворяет заданному критерию принятия решения (6), то фрагментам присваиваются одинаковые метки.

Существует еще один подход к вычислению текстурных характеристик, который предполагает обнаружение различных типов текстур с помощью локальных масок. Лавс (Laws) разработал энергетический подход, в котором оценивается изменение содержания текстуры в пределах окна фиксированного размера. В этом методе оценивается изменение содер­жания текстуры в пределах окна фиксированного размера. Для вычисления энергетических характеристик используется набор из шестнадцати масок размерами 5x5. Для получения масок используется 4 вектора: вектор L (1, 4, 6, 4, 1) предназначен для вычисления симметричного взвешенного локального среднего значения, вектор Е (-1, -2, 0, 2, 1) – для обнаружения краев, S (-1, 0, 2, 0,-1) — для обнаружения пятен, a R (1, -4, 6, -4, 1) — для обнаружения образа в виде ряби.

На первом шаге в методе Лавса предлагается устранить интенсивность влияния освещения. Для этого по изображению перемещается окно (в данном случае было выбрано окно размером 15х15), в котором из значения каждого пиксела вычитается локальное среднее значение. После обработки к изображению применяется каждая из 16 масок, в результате чего формируется 16 профильтрованных изображений. Далее строятся энергетические текстурные карты. Каждый пиксел карты представляется суммой пикселов, находящихся в области 15х15 вокруг него. После получения 16 энергетических карт некоторые симметричные карты комбинируются и формируются 9 окончательных энергетических карт.

Таким образом, каждому пикселу соответствует вектор из
9 текстурных характеристик, и сегментация проводится на основе сравнения данных векторов различных фрагментов изображения.

При структурном подходе, например, на основе мозаики Вороного, строится множество многоугольников. Многоугольники с общими свойствами объединяют в области. Для исследования общих свойств часто используют признаки – моменты многоугольников.

Сегментация с использованием мозаики Вороного состоит из трёх шагов: построения примитивов, составления мозаики, анализа элементов мозаики. Чаще всего для получения примитивов к изображению применяются фильтры, как при выделении границ. Затем выбираются точки локальных максимумов. Часто к точкам локальных максимумов применяют метод наращивания, в результате чего получают компоненты из 8-ми связных элементов. Полученные таким образом компоненты или точки локальных максимумов определяют как примитивы. Затем строится мозаичное разбиение Вороного для примитивов. Рассмотрим построение для случая, когда примитивы являются точками.

Пусть дано множество S из трех и более примитивов. Пусть не все точки лежат на одной прямой. Рассмотрим пару точек Р и Q. Построим прямую – геометрическое место точек, равно удаленных от Р и Q. Получим две полуплоскости и . Для любой точки Р можно провести такое разбиение со всеми 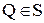. Пересечение определяет многоугольник, все точки которого ближе к Р, чем к какой-либо другой точке. Такой многоугольник называют многоугольником Вороного для данной точки. Рассматривают множество многоугольников, называемое диаграммой Вороного. Многоугольники с общими свойствами объединяют в области. Для вычисления свойств часто используют центр тяжести и момент площади многоугольника. Момент площади (p+q) – гo порядка для многоугольника относительно примитива с координатами (х, у) определяется так:

 

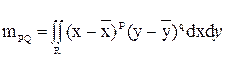, (7)

 

где (p+q)=0, 1,2,...;

– координаты центра тяжести многоугольника.

Часто используются признаки:

 

, (8)

 

, (8)

 

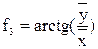, (9)

 

где 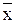, – координаты центра тяжести многоугольника.

Все выше рассмотренные методы сегментации изображений весьма приемлемы с точки зрения вычислительных затрат, однако, для каждого из них характерна неоднозначность разметки точек в реальных ситуациях из-за необходимости применения эвристик (выбор порогов, совпадения яркостей, выбор цифровых масок и т.д.).

 

 

3.Порядок выполнения работы

 

Реализовать один из методов распознавания текстур – метод матриц совпадений, метод Лавса, метод мозаик Вороного. Провести сравнение методов.

 

 

4.Контрольные вопросы и задания

 

1. Какие методы распознавания текстур известны?
2. Какие недостатки имеют эти методы?

Поделиться:

Воспользуйтесь поиском по сайту: