 |
Многочлены с вещественными коэффициентами
|
|
|
|
Многочлены и их корни
1. Многочлены: основные понятия
Теория многочленов является развитием той части школьного курса алгебры, которая начинается решением уравнения первой степени с одной неизвестной и находит своё продолжение в теории квадратных уравнений и в решении некоторых видов уравнений более высоких степеней.
Общий вид уравнения n -й степени (n – натуральное число) есть
 .
.
Обыкновенно изучение уравнений сводят к их решению. Однако представляет интерес более общая задача изучения левой части этого уравнения. При этом нам пригодятся комплексные числа.
Определение 1. Многочлен (полином) n-й степени от переменной x – это выражение вида
 . .
| (1) |
В определении нет ограничений на вид коэффициентов  . В общем случае они могут быть и комплексными числами (
. В общем случае они могут быть и комплексными числами ( ). То же самое можно сказать о переменной x.
). То же самое можно сказать о переменной x.
Многочлен (1) записан по убывающим степеням неизвестной x. При необходимости можно использовать и другие формы записи, например, по возрастающим степеням x.
Из определения следует, что любое число (кроме 0) можно рассматривать как многочлен нулевой степени ( можно трактовать как коэффициент при
можно трактовать как коэффициент при  ). Число 0 также можно рассматривать как многочлен, но это единственный многочлен, степень которого не определена.
). Число 0 также можно рассматривать как многочлен, но это единственный многочлен, степень которого не определена.
Для сокращённой записи многочленов используют обозначения 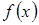 ,
,  ,
,  и т.п. При необходимости указать в сокращённой записи степень многочлена, пишут
и т.п. При необходимости указать в сокращённой записи степень многочлена, пишут  ,
,  ,
,  и т.п. В этой форме записи отражён тот факт, что многочлен можно рассматривать и как функцию переменной x.
и т.п. В этой форме записи отражён тот факт, что многочлен можно рассматривать и как функцию переменной x.
Определение 2. Равные многочлены – это многочлены, у которых равны коэффициенты при соответствующих степенях переменной x.
Определение 3. Корень многочлена 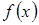 – это такое число c (в общем случае комплексное), при подстановке которого вместо переменной x многочлен
– это такое число c (в общем случае комплексное), при подстановке которого вместо переменной x многочлен 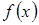 обращается в нуль.
обращается в нуль.
|
|
|
Иными словами, ( – корень
– корень 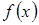 )
)  .
.
Теорема (Безу). Если многочлен 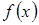 разделить на линейный многочлен
разделить на линейный многочлен  , то остаток от деления будет равен значению многочлена
, то остаток от деления будет равен значению многочлена 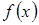 при
при  , то есть
, то есть  .
.
Математически:
 , где
, где  .
.
Важное следствие из теоремы Безу: число с тогда и только тогда является корнем многочлена, когда этот многочлен делится на  , то есть когда остаток
, то есть когда остаток  .
.
Основная теорема алгебры и следствия из неё
Теорема (основная теорема алгебры). Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Эту теорему, впервые доказанную Гауссом в конце XVIII века, мы принимаем без доказательства.
Рассмотрим следствия из основной теоремы.
Следствие 1. Если  – корень многочлена
– корень многочлена 
 , то многочлен
, то многочлен  можно разложить на произведение линейного множителя
можно разложить на произведение линейного множителя  и многочлена (n – 1)-й степени:
и многочлена (n – 1)-й степени:
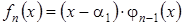 .
.
Следствие 2. Если  многочлен n -й степени, то его можно разложить в произведение n линейных множителей (
многочлен n -й степени, то его можно разложить в произведение n линейных множителей ( – коэффициент при
– коэффициент при  ):
):
 . .
| (2) |
Доказательство можно провести, применяя последовательно n раз следствие 1 к многочленам  , возникающим при выделении линейных множителей.
, возникающим при выделении линейных множителей.
Среди корней 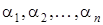 могут быть равные корни и, следовательно, среди множителей
могут быть равные корни и, следовательно, среди множителей  – равные множители. Объединим равные множители. Тогда разложение (2) можно переписать в виде
– равные множители. Объединим равные множители. Тогда разложение (2) можно переписать в виде
 , ,
| (3) |
где  и среди корней
и среди корней  уже нет равных. Говорят, что
уже нет равных. Говорят, что  – кратность корня
– кратность корня  в многочлене
в многочлене  .
.
Следствие 3. Если  – разложение многочлена на линейные множители, то с точностью до порядка сомножителей это единственное разложение такого типа.
– разложение многочлена на линейные множители, то с точностью до порядка сомножителей это единственное разложение такого типа.
Следствие 4. Если  – многочлен n -й степени
– многочлен n -й степени  , то он имеет n корней (если каждый корень считать столько раз, какова его кратность).
, то он имеет n корней (если каждый корень считать столько раз, какова его кратность).
Формулы Виета
Рассмотрим многочлен
 . .
| (4) |
Если 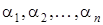 – его корни, то
– его корни, то  можно представить в виде
можно представить в виде
|
|
|
 . .
| (5) |
Перемножая линейные множители и сравнивая коэффициенты в (4) и (5), получаем формулы Виета:
 ;
;
 ;
;
 ;
;
………………………………………………
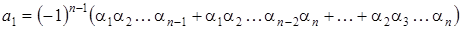 ;
;
 .
.
При  эти формулы Виета для многочлена
эти формулы Виета для многочлена  приобретают привычный со школы вид (
приобретают привычный со школы вид ( и
и  – корни многочлена):
– корни многочлена):
 ;
;  .
.
При  получим формулы Виета для кубического многочлена
получим формулы Виета для кубического многочлена  :
:
 ;
; 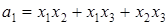 ;
;  .
.
Многочлены с вещественными коэффициентами
Всё, что было сказано выше, справедливо для многочленов, у которых коэффициенты  произвольные числа, в частности, и комплексные. Перейдём к рассмотрению более узкого, но практически важного класса многочленов – многочленов с вещественными коэффициентами.
произвольные числа, в частности, и комплексные. Перейдём к рассмотрению более узкого, но практически важного класса многочленов – многочленов с вещественными коэффициентами.
Определение. Многочлен с вещественными коэффициентами – это многочлен, у которого все коэффициенты  – вещественные числа.
– вещественные числа.
Теорема. Если комплексное число 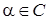 – корень многочлена с вещественными коэффициентами
– корень многочлена с вещественными коэффициентами 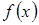 , то сопряжённое число
, то сопряжённое число  также является корнем данного многочлена.
также является корнем данного многочлена.
Иными словами, комплексные корни многочлена попарно сопряжены.
Теорема. Если комплексные числа  – корни многочлена с вещественными коэффициентами
– корни многочлена с вещественными коэффициентами 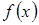 , то их кратности равны.
, то их кратности равны.
Теорема. Если 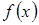 – многочлен с вещественными коэффициентами, то его можно представить (и притом единственным с точностью до порядка множителей образом) в виде произведения старшего коэффициента
– многочлен с вещественными коэффициентами, то его можно представить (и притом единственным с точностью до порядка множителей образом) в виде произведения старшего коэффициента  , линейных
, линейных  и квадратичных
и квадратичных  множителей:
множителей:
 . .
| (6) |
Достаточно очевидно, что в этом разложении линейные множители соответствуют вещественным корням  многочлена
многочлена 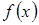 (
( – кратность корня
– кратность корня  ). Квадратичные множители соответствуют парам сопряжённых комплексных корней
). Квадратичные множители соответствуют парам сопряжённых комплексных корней 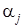 и
и  , причём в соответствии с формулами Виета
, причём в соответствии с формулами Виета  ,
,  (
( – кратность корней
– кратность корней 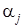 и
и  ). Очевидно, что
). Очевидно, что  .
.
Определение. Неприводимый многочлен – это многочлен с вещественными коэффициентами, который невозможно разложить на произведение многочленов с вещественными коэффициентами меньшей степени.
Среди многочленов с вещественными коэффициентами и с  неприводимыми являются лишь линейные и частично квадратные многочлены. Среди квадратных многочленов неприводимыми являются те, которые не имеют вещественных корней. Например, многочлен (6) представлен в виде произведения неприводимых многочленов.
неприводимыми являются лишь линейные и частично квадратные многочлены. Среди квадратных многочленов неприводимыми являются те, которые не имеют вещественных корней. Например, многочлен (6) представлен в виде произведения неприводимых многочленов.
|
|
|


