Понятие многочлена. Операции над многочленами.

Глава 2. Многочлены и рациональные дроби

Многочлены.

Понятие многочлена. Операции над многочленами.

1.1.1. Определение. Пусть F — некоторое числовое множество (например, это может быть множество действительных чисел R или множество комплексных чисел C). Тогда выражение f (x) вида

a ₀ xⁿ + a ₁ x^{n - 1}+...+ a_{n -1} x + a_n, (1.1.1)

где a ₀, a ₁,..., a_{n -1}, a _n — элементы множества F, x — некоторая переменная величина из, вообще говоря, произвольного (необязательно F) числового множества, называется многочленом над F. При этом, если a ₀¹0, то n называется степенью многочленаf (x) и обозначается через ст. f (x).

Многочлены будем обозначать также через g (x), h (x) и т.д., иногда снабжая их индексами: f ₁(x), f ₂(x) и т.д.

Иногда многочлен будем записывать в виде

a_nxⁿ + a_{n -1} x^{n - 1}+...+ a ₁ x + a ₀. (1.1.1¢)

Наконец, для того, чтобы подчеркнуть степень многочлена, его обозначают через P_n (x), Q_m (x) и т.д. Здесь n и m - степени соответственно P_n (x) и Q_m (x).

Многочлен может быть записан не только в виде (1.1.1) и (1.1.1¢), то есть в порядке понижения степеней, но и в произвольном порядке их следования. Если многочлен имеет вид (1.1.1) (соответственно, (1.1.1¢)), то говорят, что он записан в стандартном виде.

Любое ненулевое число из F можно рассматривать как многочлен нулевой степени, а число нуль — как многочлен неопределенной степени.

Если какой-либо коэффициент a_i у многочлена отрицателен, то принято вместо знака «+» в обозначении многочлена ставить соответствующий знак «-». Например, пишут не 3 x ³+(-4) x ²+ x +(-2), а 3 x ³-4 x ²+ x -2. Если какой-либо коэффициент a_i =0, то соответствующий член многочлена опускают. Так, пишут не 3 x ⁵+0 x ⁴+0 x ³-4 x ²+0 x -2, а 3 x ⁵-4 x ²-2.

1.1.2. Упражнение. Указать коэффициенты и степени многочленов:

а) f (x)=3 x ⁵-4 x ²+ x -2;

б) f (x)=- x ³- x +2;

в) f (x)=3 x ⁵+2 x ²-1;

г) f (x)= x ⁷;

д) f (x)=-3;

е) f (x)=(a ²-9) x ²+(a -3) x +(a -3);

ж) f (x)=(a ²-4) x ³+(a -2) x ²+3;

з) f (x)=(a ²-3 a +2) x ³+(a -1) x ²+(a -2) x +5;

и) f (x)=(a ³- a) x ²+ a (a +1) x + a.

Решение. а) В обозначениях (1.1.1) имеем a ₀=3, a ₁=0, a ₂=0, a ₃=-4, a ₄=1, a ₅=-2. Степень многочлена f (x) равна 5.

е) Если a ¹±3, то a ₀= a ²-9, a ₁= a -3 и a ₂= a +3, а степень g (x) равна 2. Если a =-3, то a ₀=0, a ₁=-6, a ₂=-6, степень g (x) равна 1. Если же а =3, то g (x) — нулевой многочлен и степень его не определена.

Ответ: а) a ₀=3, a ₁=0, a ₂=0, a ₃=-4, a ₄=1, a ₅=-2. Степень многочлена f (x) равна 5.

1.1.3. Упражнение. Записать многочлен f (x), если заданы его коэффициенты:

а) 1; -2; 3; -4; 5;

б) 2; 0; 3; -1; 0; 1; -2;

в) -5; 0; 0; 0; 0;

г) 2; -1; 3; 1; 6;

д) 1; 0; 0; 0; 0; 4;

е) 3; 0; 0; 0; 0; 0;

ж) 2; 0; -1; 0; 4; 0.

Решение. а) f (x)= x ⁴-2 x ³+3 x ²-4 x +5;

б) f (x)=2 x ⁶+3 x ⁴- x ³+ x -2;

в) f (x)=-5 x ⁴.

1.1.4. Определение. Два многочлена

f (x)= a_nxⁿ + a_{n -1} x^{n - 1}+...+ a ₁ x + a ₀, (1.1.2)

g (x)= b_mx^m + b_{m -1} x^{m - 1}+...+ b ₁ x + b ₀ (1.1.3)

называются равными, если m = n и a_i = b_i для любого индекса i. В частности, степени равных многочленов равны.

1.1.5. Упражнение. Определить, равны ли многочлены:

а) f (x)= x ⁴-2 x ³+3 x ²-4 x +5 и g (x)= x ⁴- x ³+3 x ²-4 x +5;

б) f (x)= x ⁴-2 x ³+3 x ²-4 x +5 и g (x)= x ⁴+3 x ²-4 x -2 x ³+5.

Решение. а) Данные многочлены не равны, так как коэффициенты при x ³ у них различны.

б) Данные многочлены равны, так как равны все коэффициенты при одинаковых степенях переменной.

1.1.6. Упражнение. Какие из следующих многочленов равны между собой:

f (x)=0,5 x ³+2 x ²-5 х + 7;

g (x)=lg x ³+ x ²+ х + 7;

h (x)=sin30^o× x ³+lg100× x ²- х + ;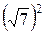

s (x)=cos120^o× x ³+ × x ²+ х + ;

p (x)=cos90^o× x +5;

q (x)=5.

1.1.7. Упражнение. При каких значениях a, b, c многочлены f (x)= ax ⁴+ bx ³+3 x ²+5 и g (x)= x ³+(c -1) x ² + 5 равны между собой?

1.1.8. Определение. Пусть n > m. Суммой многочленов (1.1.2) и (1.1.3) называется многочлен h (x), обозначаемый как f (x)+ g (x) и такой, что

h (x)= c_nxⁿ + c_{n -1} x^{n - 1}+...+ c ₁ x + c ₀,

где c_n = a_n + b_n, c_{n -1}= a_{n -1}+ b_{n -1},..., c ₁= a ₁+ b ₁, c ₀= a ₀+ b ₀. При этом если n > m, то считаем b_{m +1}, b_{m +2},... b_n равными нулю.

1.1.9. Определение. Произведением многочленов (1.1.2) и (1.1.3) называется многочлен h (x), обозначаемый как f (x) g (x) и такой, что

h (x)= d_{n + m} x^{n + m} + d_{n + m -1} x^{n + m - 1}+...+ d ₁ x + d ₀,

где d_i = , i =0, 1,..., n + m -1, n + m (например, d ₀= a ₀ b ₀, d ₁= a ₀ b ₁+ a ₁ b ₀, d ₂= a ₀ b ₂+ a ₁ b ₁+ a ₂ b ₀ и т.д.)

1.1.10. Теорема. Пусть f (x), g (x) и h (x) — многочлены. Справедливы следующие свойства операций сложения и умножения многочленов:

1. ст. (f (x)+ g (x)) не выше максимального из ст. f (x) и ст. g (x).

2. ст. (f (x) g (x))= ст. f (x)+ ст. g (x).

3. f (x)+ g (x)= g (x)+ f (x).

4. f (x)+(g (x)+ h (x))=(f (x)+ g (x))+ h (x).

5. Существует такой многочлен 0 (x), что f (x)+ 0 (x)= f (x) для любого f (x). 0 (х)называется нулевым. Роль нулевого многочлена играет 0.

6. Для любого многочлена f (x) существует многочлен g (x) такой, что f (x)+ g (x)=0. g (x) называется противоположным к f (x) и обозначается через - f (x). Ясно, что если f (x)= a ₀ xⁿ + a ₁ x^{n - 1}+...+ a_{n -1} x + a_n, то - f (x)=- a ₀ xⁿ - a ₁ x^{n - 1}-...- a_{n -1} x - a_n.

7. f (x) g (x)= g (x) f (x).

8. f (x)(g (x) h (x))=(f (x) g (x)) h (x).

9. Существует такой многочлен e (x), что f (x) e (x)= f (x) для любого f (x). e (x) называется единичным. Роль единичного многочлена играет 1.

10. (f (x)+ g (x)) h (x)= f (x) h (x)+ g (x) h (x).

1.1.11. Определение. Разностью многочленов f (x) и g (x) называется многочлен h (x), обозначаемый через f (x)- g (x) и равный f (x)+(- g (x)). Таким образом, по определению полагаем f (x)- g (x)= f (x)+(- g (x)).

1.1.12. Упражнение. Даны многочлены f (x)=3 x ³+2 x ²-5 и g (x)=4 x ⁴- x ³+2 x ²- x. Найти:

а) f (x)+ g (x), f (x)- g (x), f (x) g (x);

б) f (x) g (x)+ f ²(x).

Решение. а) Согласно определению суммы многочленов f (x) и g (x) имеем

f (x)+ g (x)=(0+4) x ⁴+(3+(-1)) x ³+(2+2) x ²+(0+(-1)) x +(-5+0)=4 x ⁴+2 x ³+4 x ²- x -5.

Далее, - g (x)=-4 x ⁴+ x ³-2 x ²+ x. Поэтому

f (x)- g (x)= f (x)+(- g (x))=-4 x ⁴+4 x ³+ x -5.

Наконец, согласно определению произведения имеем

f (x) g (x)=(3×4) x ⁷+(3×(-1)+2×4) x ⁶+(3×2+2×(-1)+0×4) x ⁵+

+(3×(-1)+2×2+0×4+(-5)×4) x ⁴+(3×0+2×(-1)+0×2+(-5)×(-1)) x ³+

+((-5)×2+0×(-1)+2×0)) x ²+((-5)×(-1)+0×0) x +(-5)×0=

=12 x ⁷+5 x ⁶+4 x ⁵-19 x ⁴+3 x ³-10 x ²+ x.

б) Заметим, что по свойству 10) имеем

f (x) g (x)+ f ²(x)=(f (x)+ g (x)) f (x).

Поэтому

f (x) g (x)+ f ²(x)=(4 x ⁴+2 x ³+4 x ²- x -5)(3 x ³+2 x ²-5)=

=12 x ⁷+14 x ⁶+16 x ⁵-15 x ⁴-27 x ³-30 x ²+5 x + 25.

Ответ:а) f (x)+ g (x)=4 x ⁴+2 x ³+4 x ²- x -5,

f (x)- g (x)=-4 x ⁴+4 x ³+ x -5,

f (x) g (x)=12 x ⁷+5 x ⁶+4 x ⁵-19 x ⁴+3 x ³-10 x ²+ x.

б) f (x) g (x)+ f ²(x)=12 x ⁷+14 x ⁶+16 x ⁵-15 x ⁴-27 x ³-30 x ²+5 x + 25.

1.1.12. Упражнение. Даны многочлены f (x)=2 x ³-3 x ²+7 х +1 и g (x)=3 x ²+2 x +5. Наиболее рациональным способом найти:

а) f (x)± g (x), f (x) g (x);

б) f (x) g (x)+ f (x), f ²(x)- f (x).

1.2. Делимость многочленов.

1.2.1. Теорема. Для любых двух многочленов f (x) и g (x) существуют такие многочлены q (x) и r (x), что

f (x)= g (x) q (x)+ r (x), (1.2.1)

причем степень r (x) меньше степени q (x) или r (x)=0. Многочлены q (x) и r (x) определяются однозначно.

Многочлен q (x) называется частным от деленияf (x) наg (x), а r (x) — остатком.

Укажем два метода нахождения частного и остатка.

1. Метод деления “ уголком ”. Этот метод проиллюстрируем на следующем примере.

1.2.2. Пример. Найти частное от деления многочлена f (x)=3 x ⁴-2 x ³+ x ²- x -1 на многочлен g (x)= x ²-3.

Решение. Будем вести запись процесса деления аналогично записи деления “уголком” целых чисел, пронумеровав каждый этап деления в круглых скобках. Итак:

(1) 3 x ⁴-2 x ³+ x ²- x -1| x ²-3

3 x ² (берем по 3 x ² )

 

(2) _3 x ⁴-2 x ³+ x ²- x -1| x ²-3

(умножаем 3 x ² на g (x)) ® 3 x ⁴-9 х ² 3 x ²

(вычитаем из f (x) 3 x ⁴-9 х ²)® -2 x ³+10 x ²- x -1

 

(3) _3 x ⁴-2 x ³+ x ²- x -1| x ²-3

3 x ⁴-9 х ² 3 x ²-2 х (берем по -2 x)

_-2 x ³+10 x ²- x -1

(умножаем -2 x на g (x)) ® -2 x ³+6 х

(вычитаем -2 х ³+6 х из -2 x ³+10 х ²- х -1)® 10 x ²- x -1

 

(4) _3 x ⁴-2 x ³+ x ²- x -1| x ²-3

3 x ⁴-9 х ² 3 x ²-2 х +10(берем по 10)

-2 x ³+10 x ²- x -1

-2 x ³+6 х

_10 x ²- x -1

(умножаем 10 на g (x)) ® 10 x ²-30

-7 х +29 остаток

Таким образом, частное от деления q (x)=3 x ²-2 х +10, остаток r (x)=-7 х +29. При этом 3 x ⁴-2 x ³+ x ²- x -1=(x ²-3)(3 x ²-2 х +10)+(-7 х +29).

2. Метод неопределенных коэффициентов также проиллюстрируем на предыдущем примере. Так как ст. f (x)=4 и ст. g (x)=2, то ст. q (x)=2, поэтому q (x)= аx ²+ bх + c. Далее, ст. r (x)<ст. g (x), поэтому r (x)= dx + e. Следовательно, равенство (1.2.1) для данных многочленов (f (x) и g (x)) и искомых (q (x) и r (x)) принимает вид

3 x ⁴-2 x ³+ x ²- x -1=(x ²-3)(аx ²+ bх + c)+(dx + e). (1.2.2)

Выполнив операции в правой части и приравняв коэффициенты при одинаковых степенях х, получим систему

решая которую, получаем

то есть имеем q (x)=3 x ²-2 х +10 и r (x)=-7 х +29.

1.2.3. Упражнение. Выполнить деление с остатком (двумя методами):

а)2 x ⁴-3 x ³+4 x ²-5 х +6 на x ²-3 x +1;

б) x ³-3 x ²- x -1 на 3 x ²-2 x +1;

в) x ⁴-2 x ³+4 x ²-6 х +8 на х -1;

г) 2 x ⁵-5 x ³-8 x на х +3;

д)4 x ³+ x ² на х +1+ i;

е) x ³- x ²- х на х -1+2 i.

1.2.4. Определение. Если в представлении (1.2.1) r (x)=0, то говорят, что f (x) делится на g (x) нацело или что g (x) делитf (x).

1.2.5. Упражнение. При каких значениях а многочлен f (x) делится на многочлен g (x).

а) f (x)= х ⁴+ ах +6, g (x)= х ²+2;

б) f (x)= x ⁶+ x ³+ а, g (x)= x ³+2.

Р е ш е н и е. а) Разделим “уголком”:

_ х ⁴+ ах +6 | х ²+2

x ⁴+2 x ² x ²+(a -2)

_(a -2) x ²+6

(a -2) x ²+2(a -2)

6-2(a -2)

Таким образом, f (x) делится на g (x), если остаток 6-2(a -2)=0, откуда а =5.

Ответ: а) при а =5.

Корни многочленов.

1.3.1. Определение. Если

f (x)= a_nxⁿ + a_{n -1} x^{n - 1}+...+ a ₁ x + a ₀ — (1.3.1)

многочлен над числовым множеством F, c Î F, то

f (a)= a_naⁿ + a_{n -1} a^{n - 1}+...+ a ₁ a + a ₀ —

элемент из F. f (a) называется значнием многочлена f (x) при х = a. Если f (a)=0, то a называется корнем многочленаf (x).

1.3.2. Упражнение. Пусть дан многочлен f (x)= x ³-3 x +2. Найти:

а) f (2); б) f (1); в) f (-2); г) f (-1); д) f (-3); е) f (4).

Решение. а) f (2)=2³-3×2+2=4; б) f (1)=1³-3×1+2=0 (в частности, 1 — один из корней многочлена f (x)= x ³-3 x +2).

Ответ: а) f (2)=4; б) f (1)=0.

1.3.3. Упражнение. Найти многочлен второй степени f (x), если:

а) f (2)=6; f (1)=1; f (-1)=9;

б) f (3)=4; f (-1)=1; f (1)=2;

в) f (-2)=6; f (-1)=-1; f (-2)=5.

Решение. а) По условию имеем, что искомый многочлен имеет вид f (x)= ax ²+ bx + c. Поэтому f (2)=4 a +2 b + c, f (1)= a + b + c и f (-1)= a - b + c. Следовательно, для нахождения коэффициентов многочлена f (x)= ax ²+ bx + c необходимо решить систему Ее решением является а =3, b =-4, c =2.

Ответ: f (x)=3 x ²-4 x +2.

1.3.4. Упражнение. Найти корни многочлена f (x):

а) f (x)=3 х -4;

б) f (x)=2 x ³+8 x ²-10 х;

в) f (x)= x ⁴-2 x ³+ x ²;

г) f (x)=- x ³+ x ²-4 x +4.

Решение. Для нахождения корней многочлена достаточно решить уравнение f (x)=0.

а) Решением уравнения 3 х -4=0 является х = . Следовательно, — корень многочлена 3 х -4.

б) Решениями уравнения 2 x ³+8 x ²-10 х =0 являются х ₁=0, х ₂=-5, х ₃=1. Следовательно, 0, -5, 1 — корни многочлена 2 x ³+8 x ²-10 х.

О т в е т: а) ; б) 0, -5, 1.

1.3.5. Теорема. a — корень многочлена f (x) тогда и только тогда, когда f (x)=(х - a) g (x) для некоторого многочлена g (x).

1.3.6. Теорема (основная теорема алгебры). Всякий многочлен n - й степени, где n >0, имеет по крайней мере один корень (действительный или комплексный).

Из теорем 1.3.5 и 1.3.6 вытекает

1.3.7. Следствие. Всякий многочлен P_n (x) n - й степени, где n >0, имеет в точности n корней; и если a ₁, a ₂, …, a_n - все корни многочлена, то его можно представить в виде

P_n (x)= a ₀(x - a ₁)(x - a ₂)…(x - a_n), (1.3.2)

где a ₀ - старший коэффициент многочлена.

1.3.8. Определение. Представление многочлена в виде (1.3.2) называется разложением его на линейные множители.

1.3.9. Упражнение. Разложить на линейные множители многочлены упражнения 1.3.4.

Решение. б) Так как корнем многочлена 2 x ³+8 x ²-10 х являются х ₁=0, х ₂=-5, х ₃=1, то 2 x ³+8 x ²-10 х =2(х -0)(х +5)(х -1), то есть

2 x ³+8 x ²-10 х =2 х (х +5)(х -1).

Ответ: б) 2 x ³+8 x ²-10 х =2 х (х +5)(х -1).

1.3.10. Упражнение. Разложить на линейные множители многочлены:

а) x ⁴-2 x ²+1;

б) x ³+2 x ²- x -2;

в) x ³-7 x -6;

г) x ⁴+ x ³-11 x ²-9 x +18;

д) x ⁵+9 x ⁴+27 x ³+23 x ²-24 x -36.

Решение. г) Заметим, что х =1 - корень многочлена. Поэтому, разделив его (многочлен) на х -1, получим

x ⁴+ x ³-11 x ²-9 x +18=(х -1)(x ³+2 x ²-9 x -18).

Далее, множитель x ³+2 x ²-9 x -18 разложим, группируя слагаемые и вынося за скобку общий множитель:

x ³+2 x ²-9 x -18=(x ³+2 x ²)-(9 x +18)= x ²(x +2)-9(x +2)=(x ²-9)(x +2).

Наконец, x ²-9=(x -3)(x +3) как разность квадратов. Окончательно получаем

x ⁴+ x ³-11 x ²-9 x +18=(х -1)(x +2)(x -3)(x +3).

Ответ: x ⁴+ x ³-11 x ²-9 x +18=(х -1)(x +2)(x -3)(x +3).

1.3.11. Определение. Если в разложении (1.3.2) многочлена какой-либо корень встречается в точности k раз, то этот корень называется корнем кратностиk. Если k =1, то корень называется простым.

С учётом кратностей корней разложение (1.3.2) можно записать в виде

, (1.3.3)

где a ₁, a ₂, …, a_k - попарно различные корни многочлена, k ₁ - кратность корня a ₁, k ₂ - кратность корня a ₂, и т.д. Ясно, что k ₁+ k ₂+…+ k_r = n.

Например,

(х -3)(х +5)(х -1)(х -1)(х +5)(х -2)(х -3)(х +5)(х -3)=(х -2)(х -3)³(х +5)³(х -1)².

Здесь 2- простой корень данного многочлена, 3 и -5 - корни кратности 3, 1 - корень кратности 2.

1.3.12. Теорема. Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами:

. (1.3.3)

При этом k ₁+ k ₂+…+ k_r +2(s ₁+ s ₂+…+ s_l)= n, и все квадратные множители x ²+ p_ix + q_i не имеют действительных корней (другими словами, их дискриминанты отрицательны: -4 q_i <0.

1.3.13. Определение. Представление многочлена в виде (1.3.3), где -4 q_i <0, называется разложением многочлена на неприводимые множители; соответственно, x - a_i (i =1, …, r), x ²+ p_jx + q_j (j =1, …, l) - неприводимые множители многочлена.

1.3.14. Упражнение. Разложить на неприводимые множители с действительными коэффициентами многочлены.

а) x ⁴+ x ³- x -1;

б) x ⁴+ x ³-11 x ²-9 x +18. (Указание: сгруппировать первые 2 слагаемые и 3-е, 4-е, 5-е слагаемые отдельно и заметить, что х =2 - корень многочлена).

Рациональные дроби.

Поделиться:

Воспользуйтесь поиском по сайту: