 |
Функции водоизмещения, в форме Нормана
|
|
|
|
Впервые суммарное изменение масс судна, связанное с изменением отдельных составляющих нагрузки, в математической форме описал французский кораблестроитель Жак-Огюстен Норман в 1885 г.
Будем рассматривать дифференциальную форму уравнения масс Нормана на примере следующего алгебраического уравнения масс, выраженных в функции водоизмещения:
D = Рк + Рсэу + Рсэз + Рзв + Р = рк D + рсэу  D2/3 + рсэз
D2/3 + рсэз  RD2/3 + рзвD + Р,
RD2/3 + рзвD + Р,
где Р – постоянные массы: Р = Pгр+ Pэк+ Pпров+ Pпр. вод+ Pсн.
Общий вид дифференциального уравнения масс:
D = F(D, рк , рсэу, v, C, рсэз, R, рзв) + P,
где: - F(D, рк , рсэу, v, C, рсэз, R, рзв) – сумма масс, зависящих от переменных D, рк , рсэу, v, C, рсэз, R, рзв, влияющих на абсолютное значение той или иной составляющей нагрузки:
F(D, рк , рсэу, v, C, рсэз, R, рзв) = рк D + рсэу  D2/3 + рсэз
D2/3 + рсэз  RD2/3 + рзвD
RD2/3 + рзвD
Полный дифференциал исходного выражения D = F(D, рк , рсэу, v, C, рсэз, R, рзв) + P
dD = dF(D, рк , рсэу, v, C, рсэз, R, рзв) + dP,
где: - dF(D, рк , рсэу, v, C, рсэз, R, рзв) – изменения масс, зависящих от переменных D, рк , рсэу, v, C, рсэз, R, рзв;
- dP – изменения постоянных масс.
Считая, что D, рк , рсэу, v, C, рсэз, R, рзв являются независимыми переменными, полный дифференциал можно представить путем дифференцирования исходного алгебраического уравнения в частных производных:
dD = (∂F/∂D)dD + (∂F/∂рк)dрк + (∂F/∂рсэу)dрсэу + (∂F/∂v)dv +(∂F/∂C)dC +
+ (∂F/∂рсэз)dрсэз + (∂F/∂R)dR + (∂F/∂рзв)dрзв + dP,
где:
- ∂F/∂D - частная производная функции F по водоизмещению D;
- ∂F/∂рк - частная производная функции F по измерителю массы корпуса рк;
- ∂F/∂рсэу - частная производная функции F по измерителю массы судовой энергетической установки рсэу;
- ∂F/∂v - частная производная функции F по скорости v;
|
|
|
- ∂F/∂C - частная производная функции F по адмиралтейскому коэффициенту С;
- ∂F/∂рсэз - частная производная функции F по измерителю массы судовых энергетических запасов рсэз;
- ∂F/∂R - частная производная функции F по дальности плавания R;
- ∂F/∂рзв - частная производная функции F по измерителю массы запаса водоизмещения рзв;
- dD, dрк, dрсэу, dv, dC, dрсэз, dR, dрЗв – изменения независимых переменных (изменение характеристик проектируемого судна по сравнению с характеристиками судна-прототипа);
- dP –изменения постоянных масс.
В этой формуле первый член (∂F/∂D)dD представляет собой изменение массы какого-либо раздела нагрузки, или суммы масс нескольких разделов, обусловленное приращением водоизмещения dD. При этом не имеет значения причина, по которой произошло приращение dD.
Изменение масс, представленных суммой членов
[(∂F/∂рк)dрк + (∂F/∂рсэу)dрсэу + (∂F/∂v)dv +(∂F/∂C)dC + (∂F/∂рсэз)dрсэз +
+ (∂F/∂R)dR + (∂F/∂рзв)dрЗв] = [dF]*,
представляет собой приращение водоизмещения судна [dF]*, вызванное изменением отдельных параметров (рк , рсэу, v, C, рсэз, R, рзв), от которых зависит масса того или иного раздела нагрузки.
Например, приращение скорости dv вызовет приращение масс энергетической установки [dPсэу]* = (∂Pсэу/∂v)dv и судовых энергетических запасов [dPсэз]* = (∂Pсэз/∂v)dv.
Если какой-либо из вышеперечисленных параметров остается неизменным по сравнению с прототипом, то, соответственно, оказывается равным нулю и приращение раздела нагрузки, зависящего от этого параметра.
Например, при dv = 0 приращение массы раздела нагрузки, зависящего от скорости v: [dPсэу]* = (∂Pсэу/∂v)dv = 0.
С учетом введенного обозначения полное приращение водоизмещения:
dD = (∂F/∂D)dD + [dF]* + dP
После преобразования этой формулы получаем окончательный вид дифференциального уравнения масс в форме Нормана:
dD = ηн{[dF]* + dP},
|
|
|
где ηн = 1/(1 ─ ∂F/∂D) носит наименование «коэффициент Нормана».
Как это следует из структуры формулы, коэффициент Нормана:
ηн > 1
Поэтому приращение водоизмещения dD всегда больше приращения массы какого-либо раздела нагрузки [dFi]*, вызванного изменением параметров, от которых зависит масса этого раздела, или независимой массы dР, или того и другого вместе. В последнем случае из этого правила может иметь место исключение, если приращения [dFi]* и dР имеют различные знаки.
Полное приращение массы отдельного раздела нагрузки будет равно сумме приращения массы этого раздела, связанного с приращением водоизмещения (∂Fi/∂D)dD, и приращения массы, связанного с изменением тех независимых параметров, от которых зависит масса этого раздела [dFi]*
dPi = (∂Fi/∂D)dD + [dFi]*
Для рассматриваемого состава уравнения масс полное приращение масс отдельных разделов будет следующим:
- приращение массы корпуса
dPк = (∂Pк/∂D)dD + [dFк]* = (∂Pк/∂D)dD + (∂Pк/∂рк)dрк;
- приращение массы судовой энергетической установки
dPсэу = (∂Pсэу/∂D)dD + [dFсэу]* = (∂Pсэу/∂D)dD + (∂Pсэу/∂рсэу)dрсэу + +(∂Pсэу/∂v)dv + (∂Pсэу/∂С)dС;
- приращение массы судовых энергетических запасов
dPсэз = (∂Pсэз/∂D)dD + [dFсэз]* = (∂Pсэз/∂D)dD + (∂Pсэз/∂рсэз)dрсэз + (∂Pсэз/∂v)dv + + (∂Pсэз/∂С)dС + (∂Pсэз/∂R)dR;
- приращение массы запаса водоизмещения
dPзв= (∂Pзв/∂D)dD + [dFзв]* = (∂Pзв/∂D)dD + (∂Pзв/∂рзв)dрзв;
- приращение независимых масс
dP = dPгр + dPэк + dPпров + dPпр. вод. + dPсн.
Для составления расчетных формул следует воспользоваться следующим правилом дифференцирования в частных производных.
Пусть масса какого-либо раздела Рi определяется следующей зависимостью
Рi = рiLnBm
Расчетная формула для частной производной ∂Pi/∂L
∂Pi/∂L = nрiLn-1Bm = nрiLnBm/L = nРi/L.
С учетом этого простого способа дифференцирования в частных производных можно получить расчетные формулы, необходимые для решения уравнения и нахождения искомого водоизмещения проектируемого судна.
Расчет коэффициента Нормана ηн = 1/(1 ─ ∂F/∂D)
∂F/∂D = ∂Рк/∂D + ∂Рсэу/∂D + ∂Рсэз/∂D + ∂Рзв/∂D = 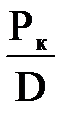 +
+  +
+  +
+ 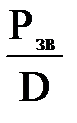
ηн = 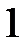 / (1–
/ (1– 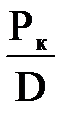 –
–  –
–  –
– 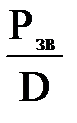 )
)
Расчет приращения водоизмещения судна [dF]*, вызванного изменением отдельных параметров v, R, C, рк , рсэу, рсэз, рзв (см. исходное алгебраическое уравнение масс)
|
|
|
[dF]*= [dFк]* + [dFсэу]* + [dFсэз]* + [dFзв]* = [(∂Pк/∂рк)dрк] + [(∂Pсэу/∂рсэу)dрсэу +
+ (∂Pсэу/∂v)dv + (∂Pсэу/∂С)dС] + [(∂Pсэз/∂рсэз)dрсэз+ (∂Pсэз/∂v)dv + (∂Pсэз/∂С)dС +
+ (∂Pсэз/∂R)dR] + [(∂Pзв/∂рзв)dрpв] =
= [ 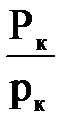 dрк] + [
dрк] + [ 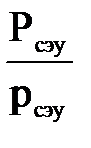 dрсэу + 3
dрсэу + 3  dv –
dv –  dC] + [
dC] + [  dрсэз + 2
dрсэз + 2  dv –
dv – 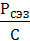 dC +
dC +
+ 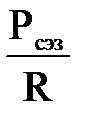 dR] + [
dR] + [  dрзв]
dрзв]
Расчет водоизмещения проектируемого судна
D = D0 + dD
После определения приращения водоизмещения dD можно найти полные изменения переменных масс, входящих в нагрузку проектируемого судна.
1. Приращение массы корпуса
dРк = (∂Pк/∂D)dD + (∂Pк/∂рк)dрк = 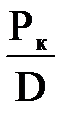 dD +
dD + 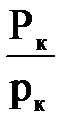 dрк
dрк
2. Приращение массы судовой энергетической установки
dРсэу = (∂Pсэу/∂D)dD + (∂Pсэу/∂рсэу)dрсэу + (∂Pсэу/∂С)dС + (∂Pсэу/∂v)dv =
=  dD +
dD + 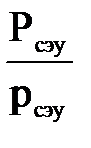 dрсэу + 3
dрсэу + 3  dv –
dv –  dC
dC
3. Приращение массы судовых энергетических запасов
dРсэз = (∂Pсэз/∂D)dD + (∂Pсэз/∂рсэз)dрсэз + (∂Pсэз/∂С)dС + (∂Pсэз/∂v)dv +
+ (∂Pсэз/∂R)dR =  dD +
dD +  dрсэз + 2
dрсэз + 2  dv –
dv – 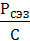 dC +
dC + 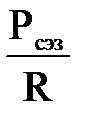 dR
dR
4. Приращение массы запаса водоизмещения
dРзв = (∂Pзв/∂D)dD + (∂Pзв/∂рзв)dрзв = 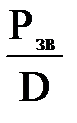 dD +
dD +  dрзв.
dрзв.
При использовании дифференциального метода для расчета нагрузки проектируемого судна приращения независимых параметров рк , рсэу, v, C, рсэз, R, рзв по сравнению с судном-прототипом определяются с учетом знака:
dрк = рк – рк0, dрсэу = рсэу – рсэу0, dv = v – v0 и тому подобное.
Полные массы разделов нагрузки проектируемого судна.
1. Масса корпуса:
Рк = Рк0 + dРк = Рк0 + 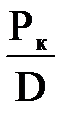 dD +
dD + 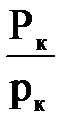 dрк..
dрк..
2. Масса судовой энергетической установки:
Рсэу = Рсэу0 + dРсэу = Рсэу0 +  dD +
dD + 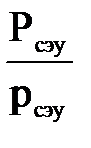 dрсэу + 3
dрсэу + 3  dv –
dv –  dC.
dC.
3. Масса судовых энергетических запасов:
Рсэз = Рсэз0 + dРсэз = Рсэз0 +  dD +
dD +  dрсэз + 2
dрсэз + 2  dv –
dv – 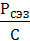 dC +
dC + 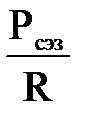 dR.
dR.
4. Масса запаса водоизмещения:
Рзв = Рзв0 + dРзв = Рзв0 + 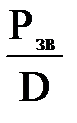 dD +
dD +  dрзв.
dрзв.
|
|
|


