 |
Пример решения задачИ с сосредоточенными нагрузками
|
|
|
|
Методические указания
к расчетно-графической работе
“Изгиб прямоугольной плиты”
Казань
УДК 539.3
ББК 22.251
Методические указания к расчетно-графической работе “Изгиб прямоугольной плиты” / Составители: Каюмов Р.А., Зиннуров Р.А., Шакирзянов Ф.Р. – Казань: КГАСУ, 2013. – 12 с.
Печатается по решению редакционно-издательского совета Казанского государственного архитектурно-строительного университета.
Приводятся постановка задачи и формулы для вычисления внутренних силовых факторов и напряжений для шарнирно-опертой по контуру прямоугольной плиты на упругом основании под действием двух сосредоточенных нагрузок.
Определяются общая схема и последовательность выполнения расчетно-графической работы, даются рекомендации для ее самостоятельного выполнения и примеры решения задач.
Ил. 6; табл. 1
Рецензент: к.ф.-м.н., профессор, заведующий кафедрой «Теоретическая механика» КГАСУ Шигабутдинов Ф.Г.
УДК 539.3
ББК 22.251
Ó Казанский государственный архитектурно-строительный университет, 2013.
Ó Каюмов Р.А., Зиннуров Р.А., Шакирзянов Ф.Р, 2013
Рассматривается задача об изгибе шарнирно опертой по контуру прямоугольной фундаментной бетонной плиты толщины h, лежащей на грунте с коэффициентом постели k. Воздействие на плиту (рис.1) представляется в виде сосредоточенных сил P 1, P 2 (например, воздействие от колонн) и постоянной распределенной нагрузки q (например, вес плиты).
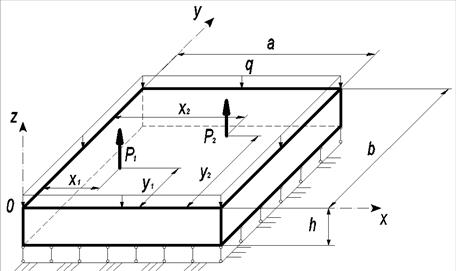
Рис. 1.
Геометрические (a, b, h, x 1, x 2, y 1, y 2), механические (модуль упругости Е= 240 т/см2 и коэффициент Пуассона 
= 0.2) и силовые параметры (
) выбираются по индивидуальному шифру из таблицы 1.
|
|
|
Таблица 1
| А | Б | В | Г | А | Б | В | Г | А | Б | В | |
| а(м) | b(м) | h(м) | x1(м) | y1(м) | x2(м) | y2(м) | P1( т ) | P2( т ) | q( т /м2) | k( т /см3) | |
| 2,2 | 5,0 | 0,1 | 0,5 | 0,2 | 2,0 | 1,8 | 0.5 | 0.001 | |||
| 2,4 | 4,8 | 0,15 | 0,6 | 0,4 | 1,8 | 1,6 | 1.0 | 0.003 | |||
| 2,6 | 4,6 | 0,2 | 0,7 | 0,5 | 1,6 | 1,4 | 1.5 | 0.005 | |||
| 2,8 | 4,2 | 0,3 | 0,8 | 0,6 | 1,4 | 1,2 | 2.0 | 0.007 | |||
| 3,0 | 3,9 | 0,4 | 1,0 | 0,8 | 1,2 | 1,0 | 2.5 | 0.01 | |||
| 3,2 | 3,5 | 0,45 | 1,2 | 1,0 | 1,0 | 0,8 | 3.0 | 0.012 | |||
| 3,4 | 3,1 | 0,5 | 1,4 | 1,2 | 0,8 | 0,6 | 3.5 | 0.015 | |||
| 3,6 | 2,7 | 0,55 | 1,6 | 1,4 | 0,6 | 0,5 | 4.0 | 0.017 | |||
| 3,8 | 2,3 | 0,6 | 1,8 | 1,6 | 0,4 | 0,4 | 4.5 | 0.018 | |||
| 4,0 | 2,0 | 0,65 | 2,0 | 1,8 | 0,2 | 0,2 | 5.0 | 0.02 |
Требуется найти выражение для прогиба плиты W (x,y), выражения для нормальных sx, sy и касательных напряжений txy и построить их эпюры. При заданных значениях 
проверить прочность плиты по критерию Г.А. Гениева (класс бетона B15, для которого 
).
Толщину плиты принять равной h = a /40, сечение бетонных свай - А св=100см2, высоту свай l =15 м, координаты первой бетонной сваи принять равными x1, y1, остальные три расположить симметрично,
Решение задачи методом Бубнова-Галеркина
Дифференциальное уравнение изгиба плиты на упругом основании записывается в виде
(1)
где 
– цилиндрическая жесткость плиты, 
– координаты сосредоточенной нагрузки, 
– описательная функция (дельта-функция Дирака, аналогичная функциям типа модуль), согласно которой сила везде равно нулю кроме точки 
.
Для решения задачи изгиба плиты используем метод Бубнова-Галеркина. В этой задаче прогибы 
, ищем в виде двойного ряда:
(2)
Легко проверить, что такой вид решения обеспечивает выполнение условия шарнирного закрепления.
Значения для A mn получаются следующим образом. Подставим соотношения (2) в уравнение (1) и умножим это уравнение на 
. Интегрирование по области, которую занимает пластина (т.е. в интервале 
), приводит к результату:
(3)
Выражения для нормальных и касательных напряжений определяются из следующих соотношений:
|
|
|
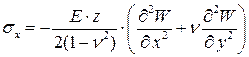, (4)
, (5)
. (6)
Расчет на прочность
Согласно критерию Г.А. Гениева, прочность бетона будет обеспечена если:
. (7)
Здесь – расчетные значения сопротивлению бетона сжатию и растяжению, 
– главные напряжения.
Главные напряжения 
, определяются по формулам:
. (8)
Максимальные сжимающие напряжения в плите возникают, согласно (4)-(6), при z=h/2, т.е. на ее верхней поверхности, а максимальные растягивающие напряжения возникают, согласно (4)-(6), при z = - h/2, т.е. на ее нижней поверхности. Подставляя (2) в (4)-(6) при z=h/2 строят эпюры напряжений в разных сечениях плиты. Это позволяет определить опасные точки и провести ее проверку прочности.
Пример решения задачИ с сосредоточенными нагрузками
Исходные данные:
Требуется найти выражение для прогиба плиты W (x,y), выражения для нормальных sx, sy и касательных напряжений txy и построить их эпюры. При заданных значениях проверить прочность плиты по критерию Г.А. Гениева.
Решение:
1. Определение прогибов
Дифференциальное уравнение изгиба плиты записывается в виде:
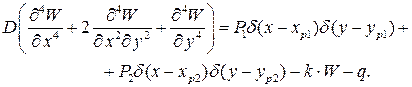(9)
В соответствии с выше изложенным, прогибы ищем в виде следующего ряда:
(10)
где
Цилиндрическая жесткость плиты равна
Для упрощения расчетов учтем только несколько членов ряда (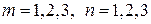
). Предварительно вычислим коэффициенты 
:
, 
,
,
,
,
,
,
,
.
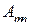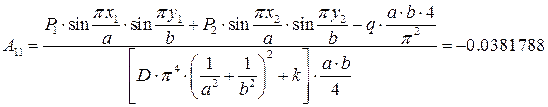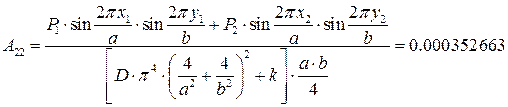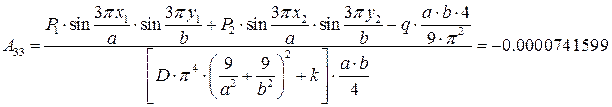Тогда из соотношения (10) получим перемещение в виде:
(11)
Определим прогибы в точках. Например, в точке 
прогиб равен 
, а в середине плиты 
: 
см. Аналогично можно найти прогибы в промежуточных точках и построить эпюру прогибов (рис. 2).
Рис. 2. Эпюры прогибов
2. Определение напряжений
Из (4)-(6) предварительно найдем производные от функции прогибов для вычисления напряжений:
(12)
Тогда напряжения на верхней поверхности плиты (при z=h/2) вычисляются из следующих соотношений:
,
, (13)
.
Из (12) и (13) видно, для ряда (10) выполняются условия равенства нулю нормальных напряжений на контуре пластины.
Как и в случае с перемещениями, определим напряжения в узлах сетки: в углу плиты при напряжения равны: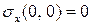 
, 
, 
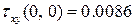т/см2 = 0.86 МПа. В середине плиты () напряжения равны 
т/см2 = 1.6 МПа, 
т/см2 = -1.1 МПа, 
т/см2 = 0.03 МПа. Аналогично можно найти напряжения во всех узлах и построить эпюры напряжений (рис. 4-6).
|
|
|
Рис. 4. Эпюра 
Рис. 5. Эпюра 
Рис.6. Эпюра 
3. Расчет на прочность
Проверим прочность бетонной плиты по критерию Гениева. Примем в расчетах класс бетона B15, для которого .
Для того, чтобы плита была прочной, функция (7), определяющая уровень напряженности малого элемента плиты, должна быть меньше единицы во всех точках. Построим эпюру функции f и найдем его наибольшее значение (рис. 7).
Рис. 7. Функция, определяющая уровень напряженности плиты
Наибольшее значение функции напряженности по критерию Гениева равно:
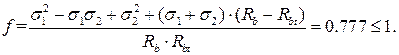
Таким образом, можно сделать вывод, что условие прочности выполняется.
Литература
1. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. – М: Высшая школа, 1990. – С. 146-174.
2. Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. – М: Стройиздат, 1974. – 316 с.
3. Доннел Л.Г. Балки, пластины и оболочки. – М: Наука, 1982. – 567 с.
4. Самуль В.И. Основы теории упругости и пластичности. – М: Высшая школа, 1982. – С. 116-134.
5. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. – М: Высшая школа, 1984. – 472 с.
6. Тимошенко С.П. Курс теории упругости. − Киев: Наукова думка, 1972. – 507 с.
7. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. − М: Наука, 1966. – 636 с.
Методические указания
к расчетно-графической работе
“Изгиб прямоугольной плиты”
Составители: д.ф.-м.н., профессор Каюмов Р.А.,
к.т.н., старший преподаватель Зиннуров Р.А.,
к.ф.-м.н., ассистент Шакирзянов Ф.Р.
Редактор
Редакционно-издательский отдел
Казанского государственного архитектурно-строительного университета
Подписано в печать Формат 60х84/16,
Заказ Печать ризографическая Усл.-печ. л. 1,0
Тираж 100 экз. Бумага офсетная № 1 Уч.-изд. л. 1,0
Печатно-множительный отдел КГАСУ
420043, Казань, Зеленая, 1
|
|
|
