 |
Определение скоростей звеньев и точек механизма
|
|
|
|
Угловые и линейные скорости звеньев механизма и шарниров механизма могут быть определены различными методами – аналитическим, графическим или графоаналитическим. Наибольшей простой и наглядностью отличается графоаналитический метод, который называется методом планов. Метод планов основан на решении векторных уравнений для линейных скоростей (или ускорений), которые составляются для конкретной структурной группы механизма. Последовательность составления таких уравнений определяется формулой строения механизма. Составление и решение векторных уравнений основано на методе Л. Эйлера.
Звенья, движущегося механизма, имеют различный характер движения – вращательное, параллельное и плоскопараллельное движение. Так движение кривошипа 1 – вращательное, поршней 3 и 5 – поступательное, а шатунов 2 и 4 – плоскопараллельное.
Из курса теоретической механики известно, что движение звеньев механизма по отношению к различным системам отчета можно рассматривать как абсолютное, переносное и относительное. В механизмах основная система отчета связана с неподвижной стойкой. Движение звена либо точки по отношению к основным системам отчета называется абсолютным. Системы отсчета могут быть подвижными, в этом случае они связаны с подвижными звеньями. Если движение звена либо точки рассматривается относительно подвижных систем отсчета, то такое движение называется относительным. Движение подвижных систем относительно неподвижных называется переносным.
Зависимости между абсолютными, относительными и переносными скоростями (ускорениями) механизма устанавливаются на основании хорошо известного из теоретической механики уравнения Эйлера
|
|
|
. (4.1)
Рассмотрим движение исходного механизма, кривошип 1 совершает вращательное движение. Величина скорости т. А определяется по выражению
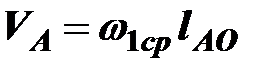, (4.2)
где 
– средняя угловая скорость кривошипа, с-1;
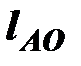– длина кривошипа, м.
Величина вектора скорости при вращательном движении направлена перпендикулярно звену АО в сторону вращения (рис.4.2).
| A |
| O |
| a nA |
| a tA |
| a A |
| VA |
| w1 |
| e1 |
| C |
| VC |
| a tC |
| a nC |
| a C |
Рис.4.2. Направление скоростей и ускорений исходного механизма
Построение плана скоростей кривошипно-ползунного механизма проводится в следующей последовательности.
1. Рассчитывается линейная скорость т. А и т. С исходного механизма (рис. 4.3) по формуле (4.2).
2. Определяется масштаб плана скоростей
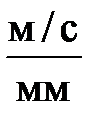, (4.2)
где pVa – отрезок, который на плане скоростей изображает скорость VA, мм. Это отрезок принимается равным pVa =50…60 мм, для V-образных двигателей его следует принять pVa =70…80 мм.
3. Определение скоростей структурной группы 2-3. Поскольку шатун 2 совершает сложное плоскопараллельное движение, то для определения скорости т. В (которая принадлежит и шатуну 2 и поршню 3) применяется уравнение Эйлера (4.1)
, (4.3)
где 
– скорость переносной среды – скорость т. А (м/с), является известной по величине (формула 4.2) и по направлению – перпендикулярна кривошипу ОА рис. 4.3;
– относительная скорость т. B вокруг т. А, является неизвестной по величине и известной по направлению – скорость 
перпендикулярна шатуну BA (рис. 4.3);
– абсолютная скорость, скорость т. В относительно неподвижной опоры т. О, выступает неизвестной по величине и известной по направлению – вектор этой скорости параллелен оси цилиндра x-x.
Векторное уравнение (4.3) содержит два неизвестных фактора – величины скоростей 
и 
, поэтому в данном виде решить его невозможно. Для его решения необходимо составить еще одно уравнение скорости т. В как принадлежащей поступательно движущемуся звену 3
|
|
|
, (4.4)
где 
– переносная скорость 
, т.к. ось цилиндра не перемещается. Здесь т. Вx – это точка, которая принадлежит оси цилиндра x-x, и временно совпадает с т. B, принадлежащей поршню;
– относительная скорость т. В относительно т. Bx, является неизвестной по величине и известной по направлению – она параллельна оси цилиндра x-x.
В данном уравнении присутствует также два неизвестных. Для этого векторные уравнения (4.3) и (4.4) следует представить в виде системы уравнений
. (4.4)
Решение этой системы проводится в таком порядке (рис. 4.3). Первоначально рассматриваем первое уравнение системы. Из произвольно выбранного полюса точки рV откладывают отрезок рVa, изображающий на плане скоростей скорость VA, который направлен перпендикулярно кривошипу ОА в сторону его вращения (рис. 4.3). Затем из конца этого вектора т. a проводят прямую перпендикулярную шатуну АВ (в заданном положении). Эта прямая является линией действия относительной скорости 
(рис. 4.3).
| Первый этап |
| Второй этап |
| Третий этап |
| План скоростей структурной группы 2-3 |
| pV |
| pV |
| pV |
| pV |
| a |
| b |
| a |
| a |
| s2 |
| a |
| b |
| ^ AB |
| // x-x |
| VA |
| VA |
| VA |
| VA |
| VB |
| VBA |
| VS2 |
| A1 |
| B1 |
| S2 |
| w1 |
| O |
| w2 |
| x |
| x |
| j1 |
| VBA |
Рис.4.3. Построение плана скоростей структурной группы 2-3
Все составляющие первого уравнения использованы, поэтому переходим к рассмотрению второго уравнения – из полюса рV проводим прямую параллельную оси x-x, которая определяет направление относительной скорости 
. Проведенные прямые пересеклись в точке b и таким способом определили положение искомого вектора рVb.
Из полученного плана скоростей полуют искомые скорости
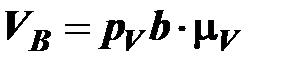м/с, (4.5)
м/с, (4.6)
где 
, 
– отрезки плана скоростей (рис. 4.3), которые определяются измерением.
Скорость центра тяжести S2 шатуна АВ определяют следующим образом. Угловая скорость шатуна w2 может быть выражена через относительные скости VBA и 
с-1, т.е.
(4.7)
Из уравнения (4.7) следует, что скорости точек S2 и B прямо пропорциональны расстоянию этих точек до точки А. Представляя вместо скоростей соответствующие отрезки из плана скоростей, уравнение (4.7) примет вид
|
|
|
,
откуда получим отрезок
мм. (4.8)
Из равенства (4.8) необходимо сделать вывод: чтобы определить отрезок плана скоростей, который изображает относительную скорость , необходимо отрезок ba плана скоростей, разделить в том же соотношении, в каком точка S2 делит звено AB. Полученный отрезок 
откладывают на плане скоростей и соединяют полученную точку s2 с полюсом плана рV. Отрезок 
представляет собой скорость точки S2, ее величина равна
м/с. (4.9)
По относительной скорости VBA вычисляют угловую скорость звена 2, которая равна
с-1. (4.10)
Направление угловой скорости определяется по направлению скорости 
. С этой целью вектор мысленно прикладывают в точке В, и его направление покажет направление угловой скорости 
(рис.4.3).
4. Определение скоростей структурной группы 4-5. Кривошип OC смещен на 180° относительно кривошипа АО исходного механизма АОС (рис. 4.4), который вращается с известной угловой скоростью w1ср. Линейная скорость точки С кривошипа равна
м/с. (4.11)
Рис. 4.4. Построение плана скоростей механизма двигателя (двух положений кривошипа)
Скорость 
перпендикулярна кривошипу ОС и направлена в сторону его вращения (рис. 4.2). Из полюса плана скоростей рV (рис. 4.4) откладывают отрезок 
, который изображает на плане скоростей скорость точки С. Длина этого отрезка определяется по зависимости
мм. (4.11)
К исходному механизму АОС и неподвижной стойке при помощи кинематических пар присоединяется структурная группа 4-5. Для определения скорости шарнира D воспользуется по-аналогии со структурной группой 2-3 уравнениями Эйлера
, (4.12)
где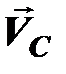 
– скорость переносной среды – скорость точки С (м/с), является известной по величине (формула 4.10) и по направлению – перпендикулярна кривошипу ОС рис. 4.4;
– относительная скорость т. D вокруг т. С, является неизвестной по величине и известной по направлению – скорость 
перпендикулярна шатуну DC (рис. 4.4);
– абсолютная скорость, скорость т. D относительно неподвижной опоры т. О, выступает неизвестной по величине и известной по направлению – вектор этой скорости параллелен оси цилиндра x-x;
|
|
|
– переносная скорость 
, т.к. ось цилиндра не перемещается. Здесь т. Dx – это точка, которая принадлежит оси цилиндра x-x, и временно совпадает с т. D, принадлежащей поршню;
– относительная скорость т. D относительно т. Dx, является неизвестной по величине и известной по направлению – она параллельна оси цилиндра x-x.
Решение этой системы проводится порядке показанном на рис. 4.4. Сперва рассматривается первое уравнение системы. Из известного полюса плана скоростей точки рV откладывают отрезок рVс, изображающий на плане скоростей скорость VС, который направлен перпендикулярно кривошипу ОС в сторону его вращения (рис. 4.4). Затем из конца этого вектора т. с проводят прямую перпендикулярную шатуну CD (в заданном положении). Эта прямая является линией действия относительной скорости 
(рис. 4.4). Слагаемые правой части первого уравнения использованы, поэтому переходим к рассмотрению второго уравнения – построения вновь начинаются из полюса рV, из которого проводим прямую параллельную оси x-x, которая определяет направление относительной скорости 
. Проведенные прямые пересеклись в точке d и таким способом определили положение искомого вектора рVd.
Из графического решения сисиемы уравнений Эйлера – план скоростей, определяют искомые скорости
м/с, (4.13)
м/с, (4.14)
где 
, 
– отрезки плана скоростей (рис. 4.4), которые определяются измерением.
Для определения скорости центра тяжести S4 шатуна СD следует первоначально определить в соответствии с формулой (4.8) величину отрезка 
мм. (4.15)
Далее полученный отрезок откладывают на плане скоростей и соединяют полученную точку s4 с полюсом плана рV. Отрезок 
представляет собой скорость точки S4, ее величина равна
м/с. (4.9)
По относительной скорости VDC угловую скорость звена 4, которая равна
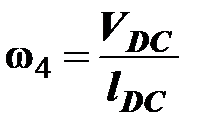с-1. (4.10)
Направление угловой скорости определяется по направлению скорости 
. С этой целью вектор 
мысленно прикладывают в точке D, и его направление покажет направление угловой скорости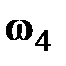 
.
Результаты вычислений скоростей структурных групп для других положений кривошипа следует представить в виде таблицы 4.1.
Таблица 4.1
|
|
|
