 |
Общий вид самосопряж диф оператора 2-ого порядка с вещ коэф.
|
|
|
|
Основное неравенство для симметричного интегрального оператора

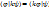 (1)
(1)
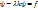 (2)
(2)
 (3)
(3)
 (4)
(4)

 (5) – резольвента интегрального оператора
(5) – резольвента интегрального оператора 

 (8)
(8)
 (9)
(9)
 (10)
(10)
Выберем μ вещественно положительным и меньшим собств. значениям оператора 

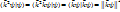 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
В равенстве (12) правая часть содержит не отрицательные слагаемые, их сумма не отрицательна
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18) – это неравенство наз основным неравенством для симметричного интегрального оператора
(18) – это неравенство наз основным неравенством для симметричного интегрального оператора
70.Пример вычисления преобразования Фурье.
 (1)- функция Грина.
(1)- функция Грина.
Рассмотрим функцию вида:
 (2)
(2)
 (3) отсюда следует
(3) отсюда следует
 (4)
(4)
 (5)
(5)
 (6)
(6)
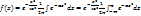 (7)
(7)
 (8)
(8)
| F(k) | 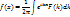
|
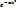
| 
|

 (9)
(9)
 (10)
(10)
Обратное преобразование дает исходную функцию.
Переход от экспоненциального ряда Фурье к интегралу Фурье.
 (1)
(1)
 (2)
(2)
 (3)
(3)
Если подставить (3) в (2), то получим:
 (4)
(4)
С увеличением l расстояние между  уменьшается.
уменьшается.
 (5)
(5)
 (6)
(6)
 (7)
(7)
l стремиться к  , а
, а  к 0.
к 0.
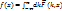 (8)
(8)
 (9) – интегральная формула Фурье
(9) – интегральная формула Фурье
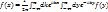 (10)
(10)
 (11) – прямое преобразование Фурье
(11) – прямое преобразование Фурье
 (12) – обратное преобразование Фурье
(12) – обратное преобразование Фурье
Замечание:
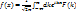 (13)
(13)
 (14)
(14)
Если в преобразованиях Фурье ввести замету 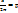 , то получим:
, то получим:
 (15)
(15)
 (16)
(16)
Многократные преобразования Фурье
 Зафиксируем
Зафиксируем  , тогда:
, тогда:
 (1)
(1)
 (2)
(2)
 (3)
(3)
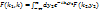 (4)
(4)
Если подставить (3) в (1), то
 (5)
(5)
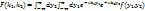 (6)
(6)
 (7)
(7)
 (8)
(8)
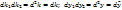 (9)
(9)
 (10)
(10)

 (11)
(11)
 (12)
(12)


Если n измерений, то
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
Случай когда есть одна временная переменная и 3 переменных по координате:
 (18)
(18)
 (19)
(19)
Однородная задача Коши для ур-ния теплопроводности и преобразование Фурье
 (1)
(1)
 (2)
(2)
Ищется температура в бесконечно длинном стержне в каждый момент времени.
 (3)
(3)
 (4)
(4)
Применим это преобразование Фурье для нашей задачи:
 (5)
(5)
 (6)
(6)
Если (5) и (6) подставить в ур-ние (1), то получим:
 (7)
(7)
 (8) – результат применения преобразования Фурье
(8) – результат применения преобразования Фурье
|
|
|
 (9)
(9)
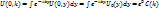 (10)
(10)
 (11)
(11)
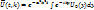 (12)
(12)
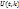 подставим в (3) и получаем:
подставим в (3) и получаем:
 (13)
(13)
 (14) – функция Грина однородной задачи Коши для ур-ния теплопроводности
(14) – функция Грина однородной задачи Коши для ур-ния теплопроводности
 (15)
(15)
Явный вид функции грина и решение однород задачи Коши для ур-ния теплопроводности.
 (1) – явный вид однородной задачи Коши
(1) – явный вид однородной задачи Коши
 (2)
(2)
Функция Грина, полученная в виде (1) имеет след интересное св-во:
 (3)
(3)
Независимость этой величины от времени означает закон сохранения энергии.
 (4)
(4)
 (5)
(5)
 (6)
(6)
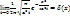 (7)
(7)
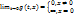 (8)
(8)
 (9)
(9)
 (10)
(10)
| F(k) | 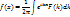
|

|
 (11)
(11)
Решение однород задачи Коши для ур-ния колебаний методом преобразования Фурье
 (1)
(1)
 (2) –НУ
(2) –НУ
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
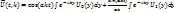 (10)
(10)
Подставляя (10) в (3) получаем окончательно:
 (11)
(11)
Определим функцию Грина однород задачи Коши для ур-ния колебаний след образом:
 (12) – это и есть функция Грина однород задачи Коши для ур-ния колебаний.
(12) – это и есть функция Грина однород задачи Коши для ур-ния колебаний.
 (13)
(13)
 (14)
(14)
49. Метод разделения переменных для ур-ний с переменными коэф.
 (ГУ) (1);
(ГУ) (1);
 =
=  (2) – оператор вычисления второй производной;
(2) – оператор вычисления второй производной;
 (ГУ) (3)
(ГУ) (3)
Для стержня переменного сечения:
с(x)  (4)
(4)
Рассмотрим случай когда источников тепла нету и температура среды=0:
с(x)  (5).
(5).
 ;
;
Подставим и преобразуя выражение получим:
 ;
;
с(x)  -
-  (8);
(8);
 (9) – ГУ
(9) – ГУ
Задачи на СЗ для матричных операторов.
L- матрица размера n*n
 =λ
=λ  =
= 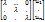 (1)
(1)
Λ есть СЗ матрицы L, а вектор  есть СВ.
есть СВ.
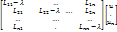 =0 (2)
=0 (2)
det  (3) – условие разрешимости
(3) – условие разрешимости
(-λ)ⁿ+SpL 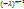 +…+detL (4)
+…+detL (4)
Основная теорема алгебры: всякое алгебраическое ур. n -й степени имеет ровно n- корней с учетом их кратности.
Запишем с помощью индексов:
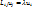 ;
; 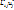 =
= 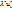 (5)
(5)
Тогда получаем:
 (6)
(6)
Преобразуем во 2-ом равенстве в левой части, тогда получим:
 =
= 
Условие вещественности:
λ = 

 =
=  (8) –выполняется всегда, если
(8) –выполняется всегда, если 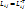 (9)
(9)
Достаточным условием для λ =  явл
явл 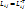 .
.
 =L (10)
=L (10) 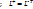 (11)-эрмитово сопряжение матрицы
(11)-эрмитово сопряжение матрицы
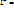 L
L  λ
λ  (12)
(12)
Матрица, кот совпадает со своей эрмитово-сопряженной матрицей,наз эрмитовой.
Матрицы Паули явл эрмитовыми:
 (13)
(13)
Св-ва:
 (14);
(14);  (15);
(15);
P=LM (16);  (17);
(17);  (18);
(18);  (19)
(19)
|
|
|
 (20)
(20)
Ортогональность СВ эрмитовой матрицы.
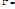 L – эрмитова матрица.
L – эрмитова матрица.
Справедливы соотношения переброса
|U> -столбец <U|- строка
<v|Lu>=< 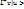 <Lv|u>=<v|
<Lv|u>=<v|  для люб матрицы
для люб матрицы
 =
=  (2)
(2)
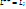
Для эрмитовой матрицы соотношения переброса запишутся в след виде:
< v|Lu>=<  (3)
(3)
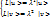 (4)
(4)
|  >;
>; 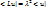 (5)
(5)
 (6)
(6)
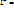 L
L
Если в (6) из первого вычтем второе, то получим:
0=(λ₁-λ₂)<v|u > (7) <v|u> =0 (8)
Сопряженные и самосопряженные диф операторы.

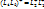 (1)
(1)
Определим сопряженный диф. оператор след. тезисами:
1)  =f(x) то
=f(x) то  =
=  (2)
(2)
2) 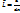 то
то  (3)
(3)
3)  то
то  =
=  ₁+
₁+  ₂(4)
₂(4)
4)  то
то  =
=  ₁
₁  ₂ (5)
₂ (5)
Рассмотрим примеры: 1)  =i
=i  (6)
(6)
 i
i  (7)
(7)
2)  (8)
(8)
 (9)
(9)
3)  (10)
(10)

Операторы, совпадающие с сопряженными наз самосопряженными операторами.

Общий вид самосопряж диф оператора 2-ого порядка с вещ коэф.
 =
=  (1) – общий вид
(1) – общий вид
 -вещественны
-вещественны

 ;
;  (3)
(3)
Используя это мы имеем:
 =
=  +
+  (4);
(4);
Чтобы (1) совпадала с (4) должны выполняться след равенства:
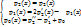 (5)
(5)
 (6)-единственное условие для вещ коэф
(6)-единственное условие для вещ коэф  =
=  ;
;  (7)
(7)

Таким образом, получаем общую ф-лу в след виде:
 (8) -общий вид самосопряженного диф. ур-я 2-го порядка с веществ коэф.
(8) -общий вид самосопряженного диф. ур-я 2-го порядка с веществ коэф.
 =
=  (9)
(9)
Эрмитовы диф операторы.
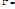 L
L

 - соотношения переброса
- соотношения переброса
Диф. оператор  наз. эрмитово сопряженным к оператору L, если для любых 2 функций из рассматриваемой системы выполняется соотношение переброса.
наз. эрмитово сопряженным к оператору L, если для любых 2 функций из рассматриваемой системы выполняется соотношение переброса.
<v(x)|L̂u(x)>=<  <v(x)|
<v(x)|  (x)>=< L̂v(x)|
(x)>=< L̂v(x)|  (1)
(1)
Оператор L наз. эрмитовым, если он совпадает со своим эрмитово сопряженным т.е. если выполняется соотношение переброса
<v(x)|L̂u(x)>=<  (2)
(2)
<v(x)|L̂u(x)>=  (3);
(3);
<v|L̂u>=<  (4);
(4);
 =0 (5)условие эрмитовости для диф операторов
=0 (5)условие эрмитовости для диф операторов
|
|
|


