 |
Явление поверхностного натяжения
|
|
|
|
Введение
В процессе проведения физического практикума необходимо научить учащегося творчески подходить к исследовательской работе, правильно выбирать методику эксперимента и измерительные приборы.
Ученики должны научиться понимать и применять теорию изучаемого явления [6].
Сознательное выполнение эксперимента, внимательность и сосредоточенность на процессе измерений, бережное отношение к приборам – необходимые условия успешного проведения
опыта [7].
Учащийся заранее должен ознакомиться с установкой, на которой ему предстоит выполнять лабораторную работу, и сделать ориентировочные измерения.
Многие учителя физики проводят в настоящее время те или иные работы, связанные с физическим экспериментом: организуют практикумы, различные физические кружки, дают домашние экспериментальные задания и т.д. Среди этих разнообразных форм обучения, приводящих к всестороннему развитию учащихся, особенно большое значение имеют классные лабораторные
работы [10].
Фронтальный метод постановки лабораторных занятий по физике в средней школе, как известно, имеет ряд весьма важных положительных сторон. Это прежде всего даёт возможность тесно связать лабораторные работы учащихся с изучаемым курсом. Благодаря фронтальному методу лабораторные занятия могут быть поставлены как введение к тому или иному разделу курса, или как иллюстрация к объяснению учителя, или как повторение и обобщение пройденного материала [13].
Таким образом, лабораторный эксперимент учащихся становится необходимым звеном в процессе обучения, значительно помогающим усвоению материала, как и демонстрационные опыты [4].
Всё вышеизложенное объясняет актуальность темы выбранной выпускной квалификационной работы: явление поверхностного натяжения входит в обязательный минимум содержания определяемый государственным образовательным стандартом, особенно в школах теоретическое обучение необходимо подтверждать экспериментом.
|
|
|
Объект исследования: процесс обучения физике в средней школе и вузе в области изучения строения и свойств жидкости.
Предмет исследования: экспериментальное определение коэффициента поверхностного натяжения жидкости.
Цель: изучение существующих методов определения коэффициента поверхностного натяжения жидкостей.
Для достижения данной цели были поставлены следующие задачи:
– углублённое изучение явления поверхностного натяжения;
– ознакомиться с существующими методами определения коэффициента поверхностного натяжения и выявить те, которые можно использовать в школьном курсе;
– отработать методику экспериментального определения коэффициента поверхностного натяжения воды методом компенсации давления Лапласа.
В первой главе рассматриваются: явление поверхностного натяжения, экспериментальные методы определения коэффициента поверхностного натяжения, а также определение коэффициента поверхностного натяжения методом компенсации давления Лапласа.
Во второй главе анализируются экспериментальные результаты данного опыта и приводится методическая разработка лабораторной работы «Измерение коэффициента поверхностного натяжения воды».
В заключении сделаны основные выводы о работе.
Глава I. Определение коэффициента поверхностного натяжения
Явление поверхностного натяжения
Изучим одно из свойств поверхности жидкости, соприкасающейся с другой средой, например с её собственным паром, с твёрдым телом, в частности со стенками сосуда.
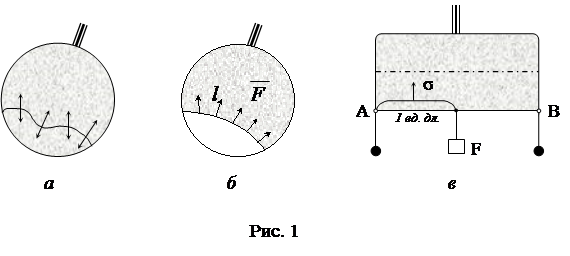
Возьмём катушку и выдуем мыльный пузырь. Как только мы отнимем катушку от рта, плёнка мыльного пузыря начнёт сокращаться, он уменьшится, а затем исчезнет. Взяв проволочное кольцо с привязанной к нему в двух толчках нитью, получим на нём мыльную плёнку (рис.1, а). На плёнке нить лежит свободно. Прорвём плёнку с одной стороны нити. Оставшаяся часть плёнки сократилась, натянув нить (рис.1, б). Получим плёнку на проволочной рамке, одна перекладина которой подвижна
(рис.1, в). В этом случае плёнка тоже сократилась, подняв перекладину [15].
|
|
|
 |
Выясним, чем обусловлено свойство поверхности жидкости сокращаться. На рис. 2 изображены три молекулы и сферы их действия. Молекулярные силы, действующие на молекулу 1 со стороны молекул, находящихся в сфере молекулярного действия, взаимно уравновешиваются. В иных условиях оказывается молекула 2 на поверхности жидкости. Над ней имеется пар жидкости, действием молекул которого можно пренебречь. При таком условии молекулярные силы, действующие на молекулу 2, оказываются неуравновешенными, их равнодействующая R направлена в глубь жидкости перпендикулярно к её поверхности. В таком состоянии находятся все молекулы поверхностного слоя толщиной в радиус сферы молекулярного действия (приблизительно слой в 1-2 молекулы).
 |
Чтобы молекула 3 оказалась в поверхностном слое жидкости, над ней надо совершить работу против сил, втягивающих её в глубь жидкости. Эта работа совершается за счёт кинетической энергии окружающих её молекул; в результате работы увеличивается потенциальная энергия поверхностного слоя жидкости.
Оказавшись в поверхностном слое, молекула станет обладать большей потенциальной энергией, чем молекулы, расположенные в глубине жидкости. Таким избыточным запасом потенциальной энергии обладают все молекулы поверхностного слоя жидкости. Эта энергия прямо пропорциональна величине поверхности жидкости.
Из курса механики известно, что начиная от атома всякая система, включая галактики, при равновесии находится в таком состоянии (из всех возможных), при котором запас её потенциальной энергии минимальный. Применительно к поверхности жидкости это означает, что данная поверхность должна сокращаться (если возможно) до минимума, тогда запас потенциальной энергии поверхностного слоя станет наименьшим. Это сокращение вызывается молекулярными силами, действующими вдоль поверхности жидкости. Они называются силами поверхностного натяжения [1].Наличием силы поверхностного натяжения и объясняется сокращение плёнки в вышеописанных опытах. Сила поверхностного натяжения, сокращая поверхностный слой, придаёт капле жидкости форму шара, вызывает слипание намоченных водой волос, слипание мокрого песка. Вектор силы поверхностного натяжения F направлен перпендикулярно к любому элементу длины линии, ограничивающей поверхность жидкости, и касательно к этой поверхности (рис. 1, в). В случае, если поверхность жидкости плоская, то вектор силы поверхностного натяжения лежит в плоскости поверхности жидкости.
|
|
|
Выясним, как можно измерить силу поверхностного натяжения. Получив мыльную плёнку на проволочной рамке, чтобы она не перемещалась, приложим к ней силу F. Сторона АВ этой рамки подвижна (рис. 1, в). Сила поверхностного натяжения плёнок (одна из которых находится по одну сторону рамки, а другая – по другую) равна весу проволоки АВ и грузика. Если так определять силу натяжения поверхностного слоя, например воды, керосина и т.д., то оказывается, что у разных жидкостей она различна. Для сравнения сил поверхностного натяжения различных жидкостей введена величина, называемая коэффициентом поверхностного натяжения. Величина, характеризующая свойство поверхности жидкости сокращаться и измеряемая силой поверхностного натяжения, действующей на единицу длины линии на поверхности жидкости, называется коэффициентом поверхностного натяжения [8].Если обозначить длину границы поверхности жидкости l, силу поверхностного натяжения одной плёнки, действующей на этой границе, - F, то коэффициент поверхностного натяжения будет
. (1)
Коэффициент поверхностного натяжения имеет наименование н/м. С повышением температуры коэффициент поверхностного натяжения чистых жидкостей уменьшается [1].
|
|
|
Асимметрия сил взаимодействия молекул переходного слоя[1] с окружающими их (в пределах объёма молекулярного действия) молекулами приводит, как известно, к представлению о наличии тангенциальных и нормальных относительно поверхности раздела фаз сил, действующих на молекулы переходного слоя [2]. Это – силы поверхностного межфазового натяжения и молекулярного давления.
Обе эти категории сил, действующих на молекулы, которые находятся на различных расстояниях от поверхности раздела фаз, не одинаковы по величине: они монотонно убывают в обоих направлениях по нормали к нормали раздела фаз.
В этом легко разобраться, рассмотрев прохождение молекулы m через поверхность раздела фаз MN (рис. 3). Пусть, например, перемещение молекулы происходит через границу раздела между жидкостью и её насыщенным паром с расстояния r радиуса молекулярного действия внутри жидкой фазы на то же расстояние в газообразной фазе [11].
Молекула переходного слоя, находящаяся на произвольном расстоянии c от фазовой границы (рис. 4), взаимодействует со всеми молекулами, находящимися в пределах шарового объёма её молекулярного действия. Результирующая этого взаимодействия равна, однако, разности суммарных взаимодействий молекулы m с молекулами, находящимися в шаровых сегментах EFG и CHD, так как взаимодействия с молекулами в шаровых поясах ACDB и ABFE уравновешиваются. Если пренебречь притяжением молекул газа, то некомпенсированным остаётся лишь притяжение молекул, заполняющих сегмент EFG. Величину этого притяжения следует считать пропорциональной числу молекул, находящихся в объёме w сегмента, а при постоянной их плотности внутри сегмента – объёму w [3].
При перемещении молекулы через фазовую границу на расстоянии 2r объём w возрастает от нуля до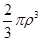 
, а затем вновь убывает до нуля. Пропорционально этому объёму изменяется и величина силы, действующих на молекулу m. Отсюда можно сделать заключение, что чем ближе молекула жидкости находится к поверхности фазы, тем больше при тепловых соударениях вероятность её выхода в газовую фазу (испарения), и чем ближе молекула пара к фазовой границе, тем больше вероятность её захвата жидкой фазой (конденсации).
Таким образом, во время перехода молекулы через фазовую границу равнодействующая молекулярных сил изменяется пропорционально объёму шарового сегмента
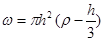, (2)
где h – высота сегмента. На рис. 5 приведена зависимость w=j(h); геометрический смысл она имеет в пределах значений h от нуля до 2r. На рис. 6 представлено изменение величины силы, действующей на молекулу при прохождении ею фазовой границы; за начало отчётов принята плоскость ОВ (рис. 3), положение молекулы определяется координатой z. Из рисунка видно, что кривая имеет максимум, соответствующей нахождению молекулы на границе фаз. Зависимость f=y(z) в равной мере относится как к поверхностному натяжению, так и к молекулярному давлению. Таким образом, s=y(z) и pm=y(z) [12].
|
|
|
До сих пор мы говорили об элементарных силах, действующих на отдельные молекулы. Однако величину поверхностного натяжения s, как известно, принято относить к единице длины контура, а молекулярное давление – к единице площади на поверхности фазы. В связи с наличием зависимости s=y(z), строго говоря, величину поверхностного натяжения (численно равную работе образования элемента поверхности) следует относить к элементарному моноатомному слою поверхностного слоя фазы, находящемуся на определённом расстоянии z от поверхности отсчёта. Обычно поверхностное натяжение относят к самому поверхностному слою фазы (z=r), где оно имеет максимальное значение. Учитывая указанные соотношения, можно было бы говорить о «среднем» значении поверхностного натяжения переходного слоя фазы, что соответствовало бы понятию «линейного напряжения переходного слоя» [2].
Что касается молекулярного давления, то ввиду наличия зависимости pm=y(z) его величину также следует представлять себе как результат суммирования элементарных сил по толщине r от переходного слоя [1].
До последнего времени не было найдено метода измерения молекулярного давления. Решение этой задачи встречает большие трудности, так как молекулярное давление по его происхождению связано с взаимодействиями молекул переходного слоя чрезвычайно малой толщины (~10-7 см) по всей поверхности фазы. Молекулярное давление доступно, однако, вычислению:
, (3)
где pBH – внешнее давление, I – механический эквивалент, Ср и Сu - молярные теплоёмкости при постоянном давлении и объёме, g - термический коэффициент объёма u. Величина pm может быть также вычислена на основании уравнения Ван-дер-Ваальса, если известны его константы.
Изменение молекулярного давления для жидкостей и твёрдых тел охватывает три порядка: 10-3¸10-5 атм. Индивидуальные вариации величины pm являются прямым следствием индивидуальных различий атомных и молекулярных структур вещества. Поэтому молекулярное давление может служить надёжным критерием интенсивности молекулярного взаимодействия.
Если известна зависимость f=y(z), то можно подсчитать работу выхода молекулы на поверхность фазы. Максимальная работа выхода [14]:
. (4)
Таким образом, увеличение поверхности связано с затратой работы; при сжатии поверхность сама совершает работу. Из этих термодинамических предпосылок и вытекает представление о поверхностном натяжении как тангенциальных силах, совершающих работу при изменении величины поверхности. Для фазовых поверхностей, имеющих кривизну, ещё Лапласом было введено представление о капиллярном дополнительном давлении р как тангенциальных силах, действующих на поверхностный слой фазы таким образом, что их результирующая направлена к центрам кривизны поверхности [14]:
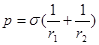. (5)
Действительно, наблюдаемые на опыте поверхностные явления протекают таким образом, как если бы поверхность находилась в состоянии квазиупругого натяжения. Такое представление весьма наглядно и облегчает решение многих задач.
Однако никакой действительной аналогии между поверхностным и упругим натяжением не существует, так как закон Гука по отношению к поверхностному натяжению не выполняется: величина деформации поверхности не зависит от s, которое в изометрических условиях изометрической величины поверхности остаётся постоянным.
К сожалению общепринятой теории возникновения поверхностных сил не существует. Имеющиеся точки зрения сводятся к следующим:
1) Выдвигается гипотеза, утверждающая, что межмолекулярные взаимодействия благодаря особой ориентации как самих молекул в поверхностном слое, так и их полей осуществляются преимущественно в направлении, тангенциальном к поверхности. Благодаря такой особой структуре поверхностного слоя возникают силы поверхностного натяжения. Иначе говоря, согласно этой точки зрения существует особая анизотропия молекулярных сил в поверхностном слое, а происхождение этих сил может быть связано с лондоновским (обменным) взаимодействием ван-дер-ваальсового типа.
2) Падение давления в жидкости по толщине поверхностного слоя при постоянном переходе от жидкости к пару, численно равное свободной поверхностной энергии, служит причиной поверхностного натяжения (Беккер) [2].
Обе эти точки зрения при их развитии наталкиваются на серьёзные трудности.
3) Н. Адам, наконец, считает, что понятие поверхностного натяжения имеет смысл лишь математического эквивалента поверхностной энергии [2]. Введение понятия поверхностного натяжения он сопоставляет с принципом возможных перемещений в статике, как чисто математическим приёмом. Так как наличие свободной энергии поверхности может быть объяснено молекулярным давлением, то, по Адаму, нет надобности задаваться вопросом, каким образом это приводит к возникновению тангенциальных сил поверхностного натяжения.
Эта точка зрения не даёт, однако, оснований отрицать, как это делает Адам, физическую реальность поверхностного натяжения.
Таким образом, подводя итоги, можно лишь сказать, что ясности в вопросе о происхождении поверхностного натяжения в настоящее время нет и что этот вопрос нуждается в теоретической разработке [16].
|
|
|
