В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Федеральное агентство по образованию

ГОУ ВПО

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Факультет непрерывного обучения

Специальность «Финансы и кредит»

 

 

КОНТРОЛЬНАЯ РАБОТА №4

по дисциплине теория вероятности и математическая статистика

Вариант 7

 

Студентки Бекмеметьева Е.А.

Личное дело № 09ФФ941717

Преподаватель Коропец А.А

 

 

Орел 2010

Задание 1

 

Данные о продолжительности телефонных разговоров, отобранные по схеме собственно-случайной бесповторной выборки, приведены в таблице:

 

Время, мин	1,5--2,5	2,5--3,5	3,5--4,5	4,5--5,5	5,5--6,5	6,5--7,5	7,5--8,5	8,5--9,5	9,5- 10,5	Итого
Число разговоров	3	4	9	14	37	12	8	8	5	100

 

Найти:

а) границы в которых с вероятностью 0,9973 заключена средняя продолжительность телефонных разговоров всех абонентов (число которых очень велико);

б) число телефонных разговоров, при котором с вероятностью 0,97 можно было утверждать, что доля всех разговоров продолжительностью не более 6,5 минут отличается от доли таких разговоров в выборке не более, чем на 0,1 (по абсолютной величине);

в) вероятность того, что отклонение той же доли в выборке от генеральной доли (см. п. б)) не превзойдет 0,05 (по абсолютной величине).

Решение

а) Найдем выборочную среднюю и выборочную дисперсию используя формулы:

 

 

К- длина интервала (1) С- середина среднего интервала (6)

Результат оформим в таблице.

 

№	интервал	средний интервал	m	U1	U1m	U1^2	U1^2m
1	1,5-2,5	2	3	-4	-12	16	48
2	2,5-3,5	3	4	-3	-12	9	36
3	3,5-4,5	4	9	-2	-18	4	36
4	4,5-5,5	5	14	-1	-14	1	14
5	5,5-6,5	6	37	0	0	0	0
6	6,5-7,5	7	12	1	12	1	12
7	7,5-8,5	8	8	2	16	4	32
8	8,5-9,5	9	8	3	24	9	72
9	9,5-10,5	10	5	4	20	16	80
Итого	-	-	100	-	16	-	330

 

 - выборачная средняя

 по таблице критических точек Лапласа t=3

 

предельная ошибка выборки

 

границы:  ; 6.16-0.542 Х₀ 6.16+0.542; 5,618 Х₀ 6.702

 

Таким образом с надежностью 0,9973 средняя продолжительность телефонных разговоров всех абонентов заключена в границах от 5,618 до 6,702

б) В качестве неизвестного значения генеральной доли р возьмем ее состоятельную оценку w, которая определяется по формуле:

 

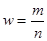 = 3+4+9+14+37/100= 0,67

m - число единиц совокупности, обладающих заданным свойством;

n - общее число единиц в совокупности.

Учитывая, что у=Ф(t) = 0,97 и t=2,17, найдем объем бесповторной выборки по формуле:

 

 - известна из пункта а).

 

При Р = 0,9545 коэффициент доверия t = 2 (по таблице значений функции Лапласа Ф(t)).

 

 разговоров

 

Вывод.Для того, чтобы обеспечить долю всех разговоров продолжительностью не более 6,5 минут необходимо отобрать в выборочную совокупность 104 разговоров.

в) Средняя квадратичная ошибка (из предыдущих расчетов) рассчитаем по формуле:

 

 

Теперь искомую доверительную вероятность находим по формуле:

 

 = Ф =Ф(1,06)=0,7109

 

Т.е. искомую вероятность того, что отклонение той же доли в выборке от генеральной доли не превзойдет 0,05 (по абсолютной величине), равна 0,7109

Задание 2

 

По данным задачи 1, используя -критерий Пирсона, уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х - продолжительность телефонных разговоров - распределена по нормальному закону. дисперсия гистограмма корреляция регрессия

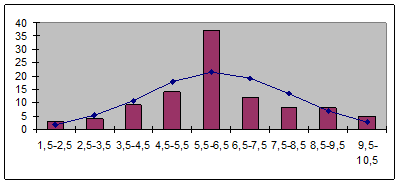
Построить на одном чертеже гистограмму и соответствующую нормальную кривую.

Решение

Для решения используем следующие формулы:

 

 ; ;

 

Результаты расчетов представим в таблице

Xi-xi+1	hi	Wi=hi/n	Zi	Zi+1	Pih,i=n*Pi
1,5-2,5	3	0.03	- -2.01-1-0.95560.0222.220.0067
2,5-3,5	4	0.04	-2.01	-1.46	-0.9556	-0.8557	0.05	5
3,5-4,5	9	0.09	-1.46	-0.91	-0.8557	-0.6372	0.109	10.9	0.339
4,5-5,5	14	0.14	-0.91	-0.36	-0.6372	-0.2812	0.178	17.8	0.812
5,5-6,5	37	0.37	-0.36	0.19	-0.2812	0.1507	0.216	21.6	10.9796
6,5-7,5	12	0.12	0.19	0.74	0.1507	0.5407	0.195	19.5	2.8846
7,5-8,5	8	0.08	0.74	1.29	0.5407	0.8029	0.131	13.1	1.99
8,5-9,5	8	0.08	1.29	1.84	0.8029	0.9342	0.066	6.6	0.3191
9,5-10,5	5	0.05	1.84	- 0.934210.0333.3
Сумма	100	1							17.33

 

Найдем число степеней свободы

 

К=r-l-1, где r - число интервалов с учетом объединенных крайних.

К = 7-2-1=4 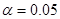 Х²_кр(0,05;4) = 9,49

 

Так как 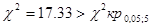, то гипотеза о нормальности данного распределения отвергается. Таким образом, случайная величина - Х - стоимость компьютера не может быть распределена по нормальному закону.

 

Гистограмма продолжительности телефонных разговоров и нормальная кривая Гаусса.

Задание 3

 

Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден. ед.) приводится в таблице:

 

y x	10	15	20	25	30	35	Итого
20	4	2					6
30		5	3				8
40			5	45	5		55
50			2	8	7		17
60			0	4	7	3	14
Итого	4	7	10	57	19	3	100

 

Необходимо:

1) Вычислить групповые средние  и построить эмпирические линии регрессии;

2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;

б) вычислить коэффициент корреляции, на уровне значимости α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;

в) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Решение:

а) Находим групповые средние

Для каждого значения х_i, т.е. для каждой строки корреляциооной таблицы вычислим групповые средние

 

, где

n_ij -частоты пар (x_i,y_j) и n_i =

m -число интервалов по переменной Y.

 

, где

 

Групповые средние:

 

1=(4*10+2*15)/6 = 11.67 2=(5*15 + 3*20)/8 = 16.88

3=(5*20+45*25+5*30)/55 = 25 4=(2*20+8*25+7*30)/17= 26.47

5=(0*20+4*25+7*30+3*35)/14= 29.64

 

Вычисленные групповые средние  поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X.

 

1=(4*20)/4= 20 2=(2*20+5*30)/7= 27.14

3=(3*30+5*40+2*50+0*60)/10= 36 4=(45*40+8*50+4*60)/57= 42.81

5=(5*40+7*50+7*60)/19=51.05 6=(3*60)/3=60

 

х/у	10	15	20	25	30	35	Итого	среднее у
20	4	2					6	11,66667
30		5	3				8	16,875
40			5	45	5		55	25
50			2	8	7		17	26,47059
60			0	4	7	3	14	29,64286
Итого	4	7	10	57	19	3	100
среднее х	20	27,14286	39	42,80702	51,05263	60

 

Эмпирическую линию регрессии у_х строим по точкам , i = 1,2,…,6.

 

2030405060
11.6716.882526.4729.64

 

Эмпирическую линию регрессии х_у строим по точкам , j = 1,2,…,6.

 

2027,143942,8151,0560
101520253035

 

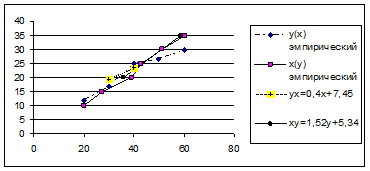
а) найдем уравнения регрессии Y по Х и Х по Y:

хi	ni	xi*ni	xi^2*ni	yj	nj	yj*nj	yj^2*nj
20	6	120	2400	10	4	40	400
30	8	240	7200	15	7	105	1575
40	55	2200	88000	20	10	200	4000
50	17	850	42500	25	57	1425	35625
60	14	840	50400	30	19	570	17100
				35	3	105	3675
	100	4250	190500		100	2445	62375

 

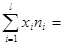 20*6+30*8+40*55+50*17+60*14=4250

20²*6+30²*8+40²*55+50²*17+60²*14=190500

10*4+15*7+20*10+25*57+30*19+35*3=2445

10²*4+15²*7+20²*10+25²*57+30²*19+35²*3=62375

4*10*20+2*15*20+5*15*30+3*20*30+5*20*40+2*20*50+45*25*40+8*25*50+4*25*60+5*30*40+7*30*50+7*30*60+3*35*60= 107850

 

Находим выборочные характеристики и параметры уравнений регрессии:

 

 76:100*10*5-(42,5-40)(24,45-25)=39,38

 

Уравнения регрессии у на х:

 

 

Уравнения регрессии у на х:

 

 

Полученные уравнения характеризуют изменение выручки (Y) при изменении тарифов на сотовую связь всех известных мобильных систем (Х) и наоборот.

Поделиться:

Воспользуйтесь поиском по сайту: