 |
Методология использования тестовых заданий в процессе изучения математики
|
|
|
|
В структуре проверки знаний на уроках математики тесты могут быть предварительными, текущими, тематическими, обобщающими, итоговыми. Так же в зависимости от используемого вида теста варьируются и временные рамки, но все же оптимальным временем для работы с тестом является 10-15 минут.
Среди всего многообразия тестов можно выделить следующие:
· задания закрытого типа с выбором ответа;
· задания на установление соответствия;
· задания на установление логической последовательности;
· задания открытого типа;
· задания свободной формы;
· комбинированные задания.
Кратко рассмотрим особенности каждого вида тестов.
Задания закрытого типа с выбором ответа предоставляют возможность учащемуся выбрать правильный ответ (несколько верных ответов) из предложенных вариантов, количество которых может варьироваться, но целесообразно включение 3-5 вариантов в одно тестовое задание. В случае использования меньшего количества вариантов ответов увеличивается вероятность угадывания верного. При включении большего количества вариантов происходят неоправданные затраты времени на ознакомление с заданием, оно становится очень массивным. Предлагаемые ответы должны направлять учащихся на анализ, продумывание и выбор правильного ответа. В качестве неверных ответов могут использоваться ошибочные ответы самих учащихся, которые обнаруживаются учителем. Обучение на примере чужих ошибок развивает способность к быстрой ориентации для выполнения правильного действия. Среди заданий данного типа выделяются следующие:
. Задания, имеющие утвердительную формулировку.
Пример. Коэффициент в произведении -7ab равен:
|
|
|
) 7;
) -7;
) -1;
) 1.
. Задания, имеющие вопросительную формулировку, требующие утвердительного ответа на вопрос.
Пример. Чему равно значение выражения 0,5a + 3,5 при a=-1:
) 4;
) 3,5;
) 3;
) -4.
. Задания, формулировка которых содержит отрицание. Следует отметить, что они сложнее предыдущих, поскольку ориентируются на более высокий уровень умственной деятельности.
Пример. Слагаемым алгебраической суммы 3a - 5b + 6c - 2d - 1 не является:
) 6c;
) -5b;
) 2d;
) 3a.
. Задания, среди вариантов ответов которого необходимо выбрать тот, который наиболее четко и полно характеризует понятие.
Пример. Чтобы привести подобные слагаемые, надо:
1. сложить их коэффициенты;
2. сложить их коэффициенты и полученный результат умножить на общую буквенную часть;
. умножить их коэффициенты на общую буквенную часть.
Суть заданий на установление соответствий состоит в определении соответствия элементов одного ряда другому. Количество элементов в двух рядах может быть как равным, так и различным. Соответствующие элементы выписываются отдельно.
Пример. Укажите подобные слагаемые:
| 3x | 18d | |
| 4ab | -m | |
| -40d | -26ab | |
| 5m | x |
В задании на установление логической последовательности, как правило, необходимо восполнить пробелы или расположить понятия в определенной последовательности.
Пример. Дополните ряд:
2a + 4a + 5b - 10a = (2a + 4a - 10a) + 5b = a(2 + 4 - 10) + 5b = … = -4a + 5b.
Задания открытого типа предоставляют учащемуся самостоятельно конструировать ответ, вставляя или удаляя необходимые слова или словосочетания.
Пример. Впишите недостающие слова:
Слагаемые, имеющие одинаковую … часть, называются … слагаемыми.
В задания свободной формы возможно составление схем, указание “лишнего” слова из перечня предложенных и пр.
Пример. Укажите выражение, значение которого при z = 5 не равно -4:
) -5z + 21; 2) z - 9; 3) -1,5z + 3,5; 4) -4z - 4.
|
|
|
Комбинированные тестовые задания могут включать элементы различных типов тестов.
Пример. Замените выражение равным:
) m + m + m + m + m;
) mmmmm;
) m + m + m + m + m + m + m;
4) mmmmmmm.) m + 5;
б) m7;
в) 5m;
г) m5;
д) 7m.
По одному и тому же учебному материалу тесты могут быть различной степени трудности, что расширяет возможности учителя в реализации дифференцированного подхода в обучении, а ребенку позволяет успешно проявить себя на уровне своих возможностей.
Работа с тестами помогает ученикам уточнить знания. Хотя последние нередко бывают “приблизительными”, но их достаточно, чтобы выбрать верный ответ и проверить свои знания. В работе с тестами совершенствуются внимание, память, стремление к улучшению результата, самоконтроль. Последнее качество развивается довольно эффективно в том случае, когда ученик имеет возможность после или во время работы с тестами открыть учебник или справочник и сопоставить свои ответы с информацией в книге. Это способствует развитию самоконтроля, умения работать со справочной литературой. Понятно, что если тест преследует цель контроля и проверки знаний, то справочная литература может быть использована после выполнения работы. В процессе закрепления учебного материала на текущем уроке ученик может пользоваться книгами. Это позволит отбросить сомнения, выделить верный ответ, который хорошо запоминается ввиду особой сосредоточенности внимания.
Тесты, как правило, отражают информацию в обобщенной форме, поэтому способствуют развитию умения обобщать знания, четко формулировать ответ.
Тестовый контроль позволяет активизировать учебный процесс. Задания для проверки знаний должны составляться с максимальным использованием проблемного подхода - взаимосвязью между поставленными вопросами, не нарушающими логику сравнения бессмысленными ответами. Правильно составленные задания и умелое их применение на занятиях, а именно в сочетании тестового контроля с традиционными методами, приучают учащихся к логике мышления, активной творческой работе, вырабатывают внимательность. Тестовые задания вызывают интерес у детей, следовательно, оказывают стимулирующее действие.
Учащиеся приучаются рассуждать, сопоставлять, анализировать, самостоятельно добывать знания. Подобные методы контроля результатов обучения, выполнение которых требует различного поворота мысли, обдумывания, самостоятельности, значительно повышают умственную деятельность и способствуют активизации учебного процесса.
|
|
|
Тесты чаще всего предлагаются на специальных карточках отдельным или всем учащимся класса. Тесты применимы и в групповой деятельности. В этом случае работа группы организуется так, чтобы учащиеся могли обсуждать выбираемый ответ. Это способствует формированию коммуникативных качеств, умения отстаивать свою точку зрения, внимательно выслушивать собеседника. Групповая работа с тестами, как правило, применяется при закреплении знаний и не преследует цели контроля достижений учащихся.
Тестовый контроль помогает реализовывать самоконтроль, самостоятельно совершенствовать и углублять знания, способствует систематической подготовке к заданиям, следовательно, активизирует познавательный интерес. Однако при всем положительном, тестовый контроль имеет свои ограничения.
Во-первых, с помощью тестового контроля можно проверять в большей степени знание фактов, теории, законов, понятий, в меньшей - практические умения и навыки. Не по всем изучаемым темам возможен тестовый контроль. Он уместен там, где надо проверить, насколько прочно усвоен материал.
Во-вторых, частое применение контролирующих программ ограничивает возможности общения с учеником, тормозит у учащегося развитие таких качеств, как умение логично и последовательно излагать свои мысли, планировать ответ, выделять главное, мало развивает речь.
Избежать эти недостатки возможно следующим образом.
Все вопросы в задании должны быть связаны с ранее изученным материалом. Необходима взаимосвязь между заданиями, что способствует формированию у обучающихся представления об изученном предмете как едином целом. Учитывая все сказанное, можно добиться хороших результатов в учебном процессе.
Наличие готового ответа приучает к шаблону и не развивает способность мыслить. Однако не все зависит от качества теста. Учащийся, анализируя ответы, должен задуматься, осмыслить изученный материал.
|
|
|
В заключении следует отметить, что, безусловно, тестовый контроль не безупречен, имеет существенные недостатки. Но знание методики составления тестовых заданий и правильное их применение позволяет учесть и исправить недостатки, поскольку методика обучения нуждается не в “опровержении” этого способа контроля, а в его усовершенствовании, чтобы присущие недостатки меньше сказывались на результате преподавания.
Заключение
Тестовый контроль знаний имеет очень широкий смысл. И для контроля на государственном уровне качества математического образования необходимо разрабатывать тесты с большой внимательностью. Такие проверки должны проводиться систематически.
Достижения уровня обязательной подготовки свидетельствуют о выполнении предъявляемых программой требований на том минимальном уровне, который является необходимым, и, одновременно, достаточным для положительной аттестации.
Тестирование проводится в нашей стране уже на протяжении нескольких лет. Тесты, как одна из форм контроля знаний, умений и навыков учащихся, применяются учителями математики на уроках и по текущим проблемам, и при проведении итоговой проверки.
Все тесты разработаны на основе спецификаций, утвержденных министерством общего и профессионального образования РФ, прошли предварительную экспериментальную проверку и доработку по результатам эксперимента.
Однако, несмотря на эти уверения, в заданиях тестов все-таки вкрадываются дефекты, а с таким положением нельзя мериться. Более важным, с точки зрения тех, кто проходит тестирование, является, на мой взгляд, то, что тесты не должны содержать:
Во-первых, заданий, допускающих двойное толкование результатов правильного их решения;
Во-вторых, заданий, при неправильном решении которых все равно получается верный ответ.
К сожалению, в тестах централизованного тестирования такого рода задания встречаются.
Вообще, авторам тестов централизованного тестирования следует обратить внимание (с позиции логики) на постановку вопросов в заданиях. Формулировки вопросов некоторых заданий содержат лишние слова, которые действительно могут сбить с толку любого логически мыслящего ученика. А так же присутствует и обратное явление: когда в формулировках вопросов нет необходимых уточняющих фраз.
Например, формулируя вопрос в задании А5: «Среднее арифметическое всех действительных корней уравнения х3 - 12х - 16 = 0 равно…»
Любой выпускник общеобразовательной школы более или менее освоивший школьный курс математики, знает, что решить уравнение - это значит найти все его корни или доказать их отсутствие. При этом имеются ввиду различные корни и действительные (поскольку комплексные числа в общеобразовательных школах по ныне действующей программе не изучаются). Лишнее словосочетание - «всех действительных»
|
|
|
Пример на обратное явление: «корни квадратного трехчлена  отрицательны, если а принадлежит промежутку
отрицательны, если а принадлежит промежутку
. (1;2)È(2;¥); 2) (1; ¥); 3) [1;2]; 4)(2; ¥); 5) [1;2) È(2; ¥).
Поскольку в формулировке вопроса отсутствует уточняющая фраза «все значения а», то любой из предложенных ответов может быть верным. При всем уважении к авторам, проявившим незаурядный талант и фантазию при составлении тестов, все же необходимо заметить, что «небрежность» подобного рода в математике не допустима.
Список использованной литературы
1. Азевич А.И.. Тестируем контрольные работы.//Математика в школе. 2000 №8
. Анастази А., Урбина С. Психологическое тестирование - СПб.: Питер, 2002. - 688 с.
. Глазков Ю.А.. Централизованное тестирование школьников //Математика в школе. 2000 №1
4. Дорофеев Г. В., Л.В. Кузнецова, и др. Оценка качества подготовки выпускников основной школы по математике. - Москва:«Дрофа», 2000
. Ивашина А.С., Т.С. Свиридова. Тестовый контроль знаний //Специалист 1997 №12
6. Карп А.Т. Даю уроки математики.- М.:Просвещение, 1992
. Майоров А.Н. Теория и практика создания тестов для системы образования. - М.: Народное образование, 2000. - 351 с.
8. Михайлычев Е.А. Дидактическая тестология. - М.: Народное образование, 2001. - 425 с.
9. Попов В.А.. Размышление учителя над итогами тестирования //Математика в школе 2000 №3
10. Самостоятельная работа учащихся в процессе обучения математике / сост. Ю.Д. Кабалевский - М.:Просвещение,1988
11. Саранцев Г.И. Упражнения в обучении математике. - М.: Просвещение, 2005. - 255с.
. Тесты, тесты, тесты… //Приложение к газете «1 сентября». Математика.1999 №2
13. Титов С.В.. Недоработки централизованного тестирования. //Математика в школе. 2000 №7
Приложение
тест контроль математика задание
Найдите значение выражения  при
при  a=-3; b=-1
a=-3; b=-1
А. 1,5 Б. -1,5 В. -0,75 Г. 0,75
1. Решите уравнение 10-7х=3-2(5х+1)
А. -2,25 Б. -5,5 В. -3 Г. 6
. Найдите корни уравнения 16-х=0
Ответ:________
4. Решите систему уравнений 
Ответ:________
5. Какое число отмечено на координатной прямой точкой А?
А.  Б.
Б. 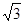 В.
В. 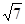 Г.
Г. 
А
0 1 2 3 4 х
. Запишите число 0,0056 в стандартном виде.
А. 5,6  Б. 5,6
Б. 5,6  В. 5,6
В. 5,6  Г. 5,6
Г. 5,6 
7. Из формулы Р=0,8h+10 выразите h.
А. h=  Б.
Б.  В. h=0,8p-10 Г.
В. h=0,8p-10 Г. 
8. Упростите выражение (а-2)2 -3а(а-1).
А. -2а2+3а-4 Б. -2а2+а+4 В. -2а2-7а+4 Г. -2а2-а+4
. В выражении 3xy2-6xy вынесете за скобки общий множитель.
Ответ:________
10. Выполните деление 
А. 
 Б.
Б.  В.
В.  Г.
Г. 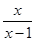
. Представьте выражение в виде дроби 
А.  Б.
Б.  В.
В.  Г.
Г. 
. Вычислите (3-4)2  35
35
А. -27 Б. -9 В.  Г. -
Г. - 
. На каком рисунке изображено решение неравенства
3х-6  5х+2?
5х+2?
А. В.
-4 X 2 X
Б. Г.
-4 X 2 X
. Решите систему неравенств 
А. -5<x<2 Б. х<2 В. х<-5 Г. х>-5
15. Поезд проходит расстояние между городами А и В за 4 ч, а автобус это же расстояние проходит за 5 ч. Скорость поезда на 20 км/ч больше скорости автобуса. Найдите скорость автобуса.
Если скорость автобуса обозначить буквой х(км/ч), То какое уравнение можно составить по условию задачи?
А.  Б.
Б.  В.
В.  Г.
Г. 
. Вычислите координаты точек пересечения графиков функции  и
и 
А. (-2;0)и(5;3) В. (3;5)и(0;-5)
Б. (3;5)и(0;-2) Г. (-2;0)и(3;5)
Найдите значение функции  при
при 
Ответ:________
17. График какой функции изображен на рисунке?
А. y=x-1 Б. y=x2-1 В. y=1-x2 Г. 
19. На рисунке изображен график функции 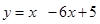 .Используя график, решите неравенство
.Используя график, решите неравенство  .
.
А. 1<x<5
Б. x<5
В .x<1
Г .x<1, x>5
Используя рисунок к заданию №19, укажите, на каком промежутке функция  убывает.
убывает.
А. х<1 Б. 1<x<5 В. x<3 Г. x>3
Дополнительная часть
Упростите выражение 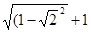 .
.
А.  Б.
Б. 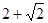 В.
В.  Г. 2
Г. 2
С помощью графиков определите, сколько корней имеет уравнение 
А. Один. Б. Два. В. Три Г. Ни одного.
|
|
|


