Изображение прямой, перпендикулярной к плоскости.

Построение линии пересечения двух плоскостей.

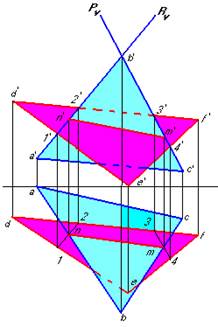
Рисунок 11 – Пересечение двух плоскостей

На рисунке 11 показано построение линии пересечения двух треугольников.

Линия пересечения треугольников АВС и DEF строится по точкам пересечения сторон одного треугольника с плоскостью другого треугольника. Построение сводится к нахождению точек М и N при помощи вспомогательных фронтально проецирующих плоскостей Р и R. Для этого заключаем сторону АВ треугольника АВС в проецирующую плоскость R. Определяем линию пересечения плоскости R с плоскостью треугольника DEF.

Это - линия 1-2. Точка М является точкой встречи прямой АВ с плоскостью DEF. Аналогично определяем точку N; заключаем сторону ВС в проецирующую плоскость Р; определяем линию пересечения плоскости Р с треугольником DEF (линия 3-4); находим точку встречи N прямой ВС с плоскостью треугольника. МN – линия пересечения треугольников. Видимость сторон треугольников определяем способом конкурирующих точек. (рис.67).

Изображение прямой, перпендикулярной к плоскости.

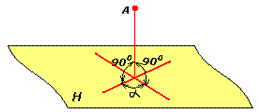
Рисунок 12 – Перпендикулярность прямой к плоскости

Известно, что прямая будет перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в данной плоскости рисунок 12. Однако прямой угол (в данном случае между прямой, лежащей в плоскости, и перпендикуляром к ней) проецируется в истинную величину (90°) лишь в том случае, если одна из его сторон параллельна плоскости проекций. Поэтому, чтобы построить на чертеже перпендикуляр к плоскости, нужно брать в ней не любые прямые, а прямые, параллельные плоскостям проекций, т.е. прямые уровня — горизонтали и фронтали. Проводить перпендикуляр нужно к этим прямым. Для того чтобы прямая была перпендикулярна к плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция — к фронтальной проекции фронтали плоскости.

Если, например, через заданную точку D необходимо провести прямую, перпендикулярную к плоскости, заданной треугольником АВС (рисунок 12), следует выполнить такие построения:

1) провести в плоскости, заданной треугольником АВС, прямые уровня — горизонталь и фронталь;

2) из горизонтальной проекции d точки D провести прямую, перпендикулярную к горизонтальной проекции а1 горизонтали; это будет горизонтальная проекция прямой перпендикуляра;

3) из фронтальной проекция d' точки D провести прямую, перпендикулярную к фронтальной проекции а'2' фронтали,— фронтальную проекцию прямой перпендикуляра. Построенная прямая и есть перпендикуляр к плоскости, заданный треугольником АВС

В рассмотренном примере на чертеже не найдено основание перпендикуляра. Чтобы это сделать, необходимо построить точку пересечения перпендикуляра с плоскостью, т.е. решить позиционную задачу на пересечение прямой с плоскостью.

При построении перпендикуляра к проецирующей плоскости (например, фронтально-проецирующей плоскости, заданной треугольником АВС) одну из его проекций — в данном случае фронтальную проекцию d'k' —проводят перпендикулярно к прямой, являющейся проекцией плоскости. Вторая проекция dk перпендикуляра параллельна оси х. В этом случае проекция прямого угла сохраняет свою истинную величину, потому что одна из его сторон (а именно, перпендикуляр DK) параллельна плоскости проекций. На рисунке изображено и основание перпендикуляра — точка K(k,k').

В случае, когда плоскость задана следами, проекции перпендикуляра к плоскости перпендикулярны к проекциям одноименных с ними следов этой плоскости рис. 72. На рис. 72 найдено и основание K(k, k') перпендикуляра к плоскости. Для этого через перпендикуляр проведена вспомогательная горизонтально-проецирующая плоскость Q (qºg_Q, f'_Q) и найдена линия пересечения ВС (bс, b'с') этой плоскости с плоскостью Р. Точка К получена в пересечении прямой ВС с перпендикуляром.