Перпендикулярность пр-х и пл-тей,пр-й и пл-ти,пл-тей.Угол м/у пр-й и пл-тью,м/у пл-ми, расст-е м/у геом.фигурами

(1)^-ть пр-й и пл-ти Df 2 пр-е наз. ^ -ми,если угол м/у ними=90⁰.

Лемма. Если одна из 2-х //-х пр-х ^ -на к 3-ей пр-й,то и др.пр-я ^ -на к этой пр-й.

Дано: a//b,a^с. Д-ть:b^с Д-во:1)MÏа,MÏb,MÏс 2)МС//с (МÎМС),МА//а.3)а^сÞÐAМС=   Дано:a//b,a^a Д-ть:b^a Д-во:1)"хÌa;a^aÞa^х. По лемме b^с2)хÌa,x-"пр-яÞb^a     Дано:a^a,b^a Д-ть:а//b Д-во:1)Предп.против.a//bÞ MÎb,MÎb1,b1//a 2)bÇb1=M, b=(b,b1) 3)a^a,то a^х(хÌa),b1//a   Дано:a,a^р,a^q,pÇq=O,pÌa, qÌa Д-ть:а^a(а^m,mÌa) Д-во:1сл:ОÎа 1)l//m,ОÎl 2)AO=ОВ 3)xÎa,xÇp=P,xÇq=Q xÇl=L 4)Т.к.p и q-сер.^-ры к АВ,     AH-^-р,АВ-наклонная,Н-осн-е ^-ра,В-осн-е накл-й,НВ-проекц. накл-й АВ на a.^ меньше"накл.

90⁰.4)b//a(по усл),а//МА(по постр)Þb//MA

5)b//MA,c//MC,Ð(MA,MC)=90⁰ÞÐ(b,c)=90⁰Þb^с

Df Пр-я наз.^-й к пл-ти,если она ^-на к "пр-й, лежащей в этой пл-ти:а^a.

Th1 Если одна из 2-х //-х пр-х ^-на к пл-ти,то и др.пр-я ^-на к этой пл-ти.

Th2 Если 2 пр-е ^ -ны пл-ти,то они //-ны.

 

b₁^a(Th1).Ч/з т.М проходят 2 пр-е b,b₁,^-ные a

Кроме этого,b₁^с и b^сÞПротиворечиеÞa//b

Пр-к Th3 Если пр-я ^-на к 2-м пересек.пр-м, леж.в пл-ти,то она ^-на к этой пл-ти.

 

то АР=ВР и AQ=BQÞDAPQ=DBPQ(по 3-м стор)

ÞÐAPQ=ÐBPQ 5)DAPL=DBPL(AP=ВР,Р-общ., ÐAPL=ÐBPL)ÞAL=BLÞDABL-равнобедр.Þ медиана LO явл.высотойÞl^a 6)l//m,l^aÞm^a

(по лемме)Þа^a.2сл:ОÏа 1)Проведем ОÎа₁,

а//а₁Þпо лемме a₁^р,a₁^qÞa₁^a.2)По Th1 a^a

(2)^-р и наклонные

Df1 Расст-ем от точки до пл-ти наз.длина ^-ра

(1) Все точки одной пл-ти равноудалены от точек др.пл-ти,если эти пл-ти //-ны.

Df2 Расст-ем м/у //-ми пл-ми наз.расст-е от " точки одной пл-ти до другой.

(2) Если пр-я //-на пл-ти,то все точки пр-й равноудалены от этой пл-ти.

Df3 Расст-е от произ.точки пр-й до пл-ти наз.расст-ем м/у пр-й и //-й ей пл-тью.

(3) Если 2 пр-е скрещ-ся,то ч/з каждую из них проходит пл-ть,//-ная др.пр-й,и только одна.

Df4 Расст-е м/у одной из скрещ.пр-х и пл-тью, проходящ.ч/з др.пр-ю //-но 1-ой,наз.расст-ем м/у скрещ.пр-ми.

Th4 Ч/з "точку пр-ва проходит пр-я,^-я к дан. пл-ти,и только одна.

Th5(о 3-х ^-рах) Пр-я,проведен.в пл-ти ч/з осн-е накл-й ^ -но к ее проекции на эту пл-ть, ^ -на и к самой наклонной.

Дано: a,АМ-накл.к a,аÌa, МÎа, а^МН Д-ть:а^AM Д-во:1)а^(АMН),т.к.а^MН(усл)

а^АН,т.к.АН^aÞ2)а^"пр-йÞа^АМ,АМÌ(АМН)

Th6(обратная) Пр-я,провед.в пл-ти ч/з осн-е накл-й ^ -но к ней, ^ -на и к ее проекции.

Df5 Проекцией точки на пл-ть наз.осн-е ^ -ра, провед.из этой точки к пл-ти,если точка не ле-жит в пл-ти.

Th7 Проекцией пр-й на пл-ть,не ^ -ную к этой пр-й,явл.пр-я.

(3)^-ть пл-тей

Df Двугран.углом наз.фигура,образован.пр-й а и 2-мя полупл-ми с общ.границей а,не принадлежащими одной пл-ти(a,b-грани,а-ребро, ÐАОВ-лин.угол)!Лин.углы дв.угла равны др.др

Df Град.мерой двугр.угла наз.град.мера его лин.угла.

Df 2 пересек.пл-ти наз. ^ -ми,если угол м/у ними равен 90⁰.

Дано: a,b,АВÌa,АВ^b, АВÇb=А Д-ть: a^b Д-во:1)aÇb=АС(АВ^АС,т.к. по услАВ^b)ÞАВ^"пр-й в пл-тиb     aÇb=A,Ð(a,b)=j.Если а//b,то Ð(a,b)=00,a^bÞÐ(a,b)=900, 00£Ð(a,b)£900

Пр-к ^-ти 2-х пл-тей Th Если одна из 2-х пл-ей проходит ч/з пр-ю, ^ -ую к др.пл-ти,то такие пл-ти ^ -ны.

2)AD^AC,ADÌbÞÐBAD-лин.угол двугр.угла. Но ÐBAD=90⁰(т.к.АВ^b)ÞУгол м/у пл-ми a и b =90⁰,т.е.a^b.

Следст. Пл-ть, ^ -ная к пр-й,по кот.пересек-ся 2 дан.пл-ти, ^ -на к кажд.из них.

(4)Углы м/у а, b

Df Под углом м/у 2-мя пересек.пр-ми понима-ют углов.меру наим.из углов,образов. этими пр-ми.

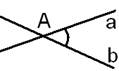
Df под углом м/у 2-мя скрещ.пр-ми понимают угол м/у 2-мя пересек.пр-ми,соотв-но //-ми зад.скрещ.пр-м:

b1//b,K1Îa,K1Îb1,Ð(a,b)=Ð(a1,b1) Нужно проверить, корректно ли Df DfÞ Докажем, что вел-на угла     А1:а1//а,b1//b A2:а2//а,b2//bÞ a1//a2, b1//b2(по пр-ку //-ти пр-х в пр-ве)

не зависит от того,как выбрана точка,ч/з кот. проводятся пр-е,соотв.//-е 2-м зад.скрещ.пр-м

 

j₁=Ð(a₁,b₁),j₂=Ð(a₂,b₂)Þj₁=j₂(по Th о рав-ве углов с соот.//-ми стор-ми)ÞDf корректно и вел-на угла не зависит от выбора точки.

Метод.зам-я:Как строить углы с привязкой на фигуру?

Возьмем тетраэдр DE × BC. Для постр-я угла м/у скрещ.пр-ми рассм.пл-ть,содерж.одну из скрещ.пр-х и нек.точку 2-й пр-й. a=(BC,E),EÎm,m//BC,

Ð (DE,BE)= Ð DEK.Используя пон-е угла м/у скрещ.пр-ми полезно расширить прим-е нек.теорем(Th о 3-х ^ -рах).Если пр-я,леж.в пл-ти, ^ -на проекции накл-й на эту пл-ть,то она ^ -на и самой наклонной,и обратно.

(5)Углы м/у а и a

Пр-я и пл-ть м.б.а)//-ны;б)пересек-ся.Пусть а^a,тогда она явл.накл-й к пл-ти.В оптике говорят о падении луча света на плоск.пов-ть, т.е.об угле м/у пр-й и ^-ром к дан.пл-ти.Но в геом.оценивая наклон пр-й к пл-ти,мы чаще говорим об угле,кот.доп-ет 1-ый до 90⁰.

Df Углом м/у пл-тью a и пр-й а,причем аÇa=А и а^a,наз.угол м/у этой пр-й и ее проекцией на пл-ть:Ð(a,a)=Ð(a,a₁),где а₁-ортогон.проекц.

Если а//a,то проекция пр-й а1//а,то в этом случае Ð(a,a)=00, 00£Ð(a,a) £900   Дано:аÇa=А,а1-проекция а на a j0=Ð(а,а1),р-произв.пр-я,рÌa, АÎр,j=(а,р) Д-ть: j0<j Д-во:1)ВР^р,РÎр 2)DАВО: sinj0=BO/AB 3)DABP:sinj=BP/AB

Th о мин-ти угла м/у пр-й и пл-ю(св-во):Ðj₀ м/у пр-й и ее проекцией на пл-ть явл.наим.из всех углов,кот.дан.пр-я образует с пр-ми,про-вед.в пл-ть a ч/з точку сеч-я дан.пр-й и пл-ти.

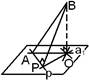
4)ВР-гип.,ВО-катет,DВРО Þ ВО/AB<BP/ABÞsinj₀<sinjÞj₀<j

Т.к.простр. мыш-е шк-ков имеет св-во закрепощаться, то необх.на простейш.геом.фигурах нах-ть постр-ем угол м/у пр-й и пл-тью, распо-лож.произвол.образом.У уч-ся ошибки при опр-и угла м/у пр-й и пл-тью возникают из-за неверн.опр-я проекции пр-й на указ.пл-ть.

Д-во:1)BL^l, LÎl 2)DABL:cosd=AL/AB 3)DALO:AL=AOcosb, DABO:AB=AO/cosg Þcosd=cosbcosg   g: g^АВ, gÇa=а, gÇb=b a,b-полупл-ти. (a,b)-лин.угол двугр.угла (а^АВ, b^АВ, aÇb) g^a, g^b

Th о 3-х косинусах. Пусть АВ-наклон.к a,АО- ее проекция на a, l-произ.пр-я,леж.на пл-ти a и проход.ч/з т.А.Пусть g=Ð(АВ,a),b-угол м/у проекцией наклон.АВ и пр-й l, d-угол,кот.обра-зует наклон-я с пр-й l:cosd=cosg×cosb

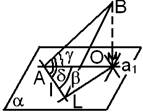
(6)Углы м/у a и b CABD-двугран.угол

 

Поделиться:

Воспользуйтесь поиском по сайту: