 |
Соотношения между параметрами ненасыщенных моделей и маргинальными суммами таблиц сопряженности. Обобщение Берча и его следствие
|
|
|
|
Модели с отсутствием влияния главного эффекта одного из факторов и независимостью двух других для таблицы сопряженности 2Х2Х2 (формулировка, проверяемая гипотеза, теоретические частоты, проверка адекватности).
1. A. (A/B) – в предположении об отсутствии влияния Z и независимостью X и Y
. 
B. (B/C) – в предположении об отсутствии влияния X.
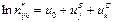
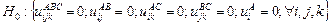
C. (A/C) – в предположении об отсутствии влияния Y.
2. A. (A/B)
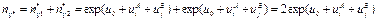
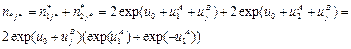
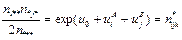
B. (B/C)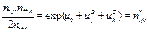 
C. (A/C) 
3. Число клеток таблицы = 8
Число параметров = 1+2+2=5
Число ограничений =2
Число степеней свободы 
Критическая область: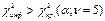 
, H0 отвергается с вероятностью ошибки α, модель адекватна
Область принятия решения: 
H0 не отвергается на уровне значимости α, модель не адекватна
Модели с отсутствием влияния главного эффекта двух факторов для таблицы сопряженности 2Х2Х2 (формулировка, проверяемая гипотеза, теоретические частоты, проверка адекватности).
1. A. (A) – в предположении об отсутствии влияния главного эффекта Y и Z
. 
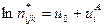
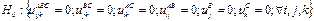
B. (B) – в предположении об отсутствии влияния главного эффекта X и Z.
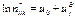
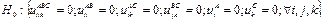
C. (C) – в предположении об отсутствии влияния главного эффекта X и Y.
2. A. (A)
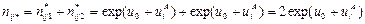
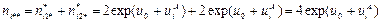
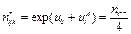
B. (B)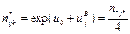 
C. (C) 
3. Число клеток таблицы = 8
Число параметров = 1+2=3
Число ограничений =1
Число степеней свободы 
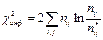
Критическая область: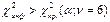 
, H0 отвергается с вероятностью ошибки α, модель адекватна
Область принятия решения: 
H0 не отвергается на уровне значимости α, модель не адекватна
Равновероятная модель для таблицы сопряженности 2Х2Х2 (формулировка, проверяемая гипотеза, теоретические частоты, проверка адекватности).
1.. 
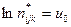
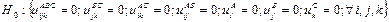2. 
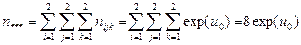
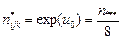
3. Число клеток таблицы = 8
Число параметров = 1
Число ограничений =0
Число степеней свободы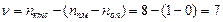 
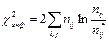
Критическая область: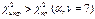 
, H0 отвергается с вероятностью ошибки α, модель адекватна
|
|
|
Область принятия решения: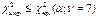 
H0 не отвергается на уровне значимости α, модель не адекватна
Иерархические логарифмически-линейные модели и принципы их построения (приведите примеры).
Иерархическая модель подчиняется следующему правилу: если в модель включен параметр, зависящий от множества n факторов, тогда модель должна включать также и все параметры, зависящие от любого подмножества из этого множества факторов.
(1) 
влечет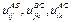 
(2) 
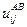влечет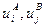 
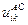влечет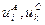 
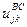влечет 
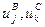(иерархия причин)
A/B включает в себя 
BC/A включает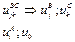 
AB/AC включает 
Пример – для 5 факторов ABCDE:
Модель А включает 
и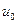 
Модель АВ включает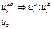 
Модель АВС включает 
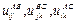
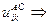
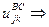
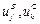
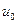
ВСЕ/А включает 
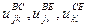
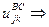
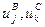
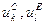
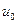
СDE/AE/BC включает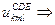 
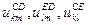
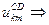
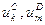
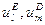
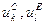
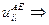
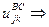
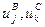
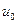
Соотношения между параметрами ненасыщенных моделей и маргинальными суммами таблиц сопряженности. Обобщение Берча и его следствие
- мера общего среднего, то есть параметр равен среднему значению натурального логарифма частот по все ячейкам таблицы сопряженности.
Главные эффекты равны разности между средним логарифмом частот по соответствующему уровню соответствующего фактора и общим средним. (Например,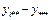 
).
2хфакторные взаимодействия равны среднему логарифму по ячейкам, соответствующим паре уровней соответствующий факторов минус средний логарифм частот по уровню 1 фактора, минус средний логарифм частот по уровню второго фактора, плюс общий средний логарифм.
И так далее, на каждом последующем уровне меняется знак.
Например,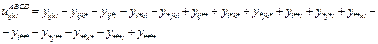 
В равновероятной модели все оцениваемые частоты ячеек равны общему объёму выборки n, деленному на число ячеек таблицы сопряженности так, что их сумма оказывается равной наблюдаемой общей частоте.
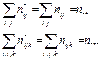
Для моделей зависимости только от фактора Х частоты, соответствующие i-й категории 1 признака равны сумме наблюдаемых частот, соответствующих этой категории, деленной на число ячеек в ней. Следовательно, сумма оцениваемых частот ячеек, соответствующих i-й категории 1 признака, оказывается равной маргинальной частоте, соответствующей этой категории.
|
|
|
Для моделей зависимости от У
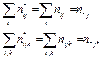
Для моделей зависимости от Z
Обобщение Берча (1963): сумма теоретических частот по определенному индексу равна сумме наблюдаемых частот по тому же индексу, если соответствующий параметр u включен в логлинейную модель.
A,B,C,D – 4 дихотомические переменные для модели, определяемой 3хфакторным взаимодействием.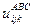 
: 
Суммирование по индексу i: (1)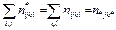 
Суммирование по индексу j: (2)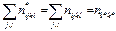 
Суммирование по индексу k: (3)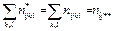 
В соответствии с обобщением Берча из (1) следует, что в модель включается ,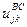
из (2)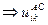 
, из (3) 
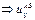Следствие обобщения Берча: включение в модель некоторого параметра, зависящего от множества n факторов, автоматически влечет включение и всех параметров, зависящих от любого подмножества из этого множества факторов.
|
|
|
