 |
Задания и указания к их выполнению
|
|
|
|
ТОНКИЕ ЛИНЗЫ
Цель работы: освоить методику получения изображений с помощью линз, научиться определять фокусное расстояние линз.
Вопросы, знание которых обязательно
для допуска к выполнению работы:
1. Что такое линза?
2. Что такое тонкие линзы?
3. Что такое точечный источник, оптический центр линзы, главная и побочная оптическая оси, фокус, фокальная плоскость и фокусное расстояние?
4. Собирающие и рассеивающие линзы.
5. Действительное и мнимое изображение предмета.
6. Какие лучи называются параксиальными?
7. Формула тонкой линзы.
8. Увеличение линзы.
9. Оптическая сила линз.
10. Основные законы геометрической оптики.
11. Построение изображений в собирающих и рассеивающих линзах для различных случаев расположения предмета относительно линзы. Для каждого случая ответьте на следующие вопросы:
а) Где будет изображение?
б) Будет ли изображение действительным или мнимым, как его наблюдать?
в) Будет ли оно увеличенным, уменьшенным или в натуральную величину?
г) Будет ли оно перевернутым или нет?
ВВЕДЕНИЕ
Линзой называется прозрачное тело, ограниченное двумя криволинейными (обычно сферическими) поверхностями или одной криволинейной и одной плоской поверхностью. Если толщина самой линзы мала по сравнению с радиусами кривизны преломляющих поверхностей, то линзу называют тонкой.
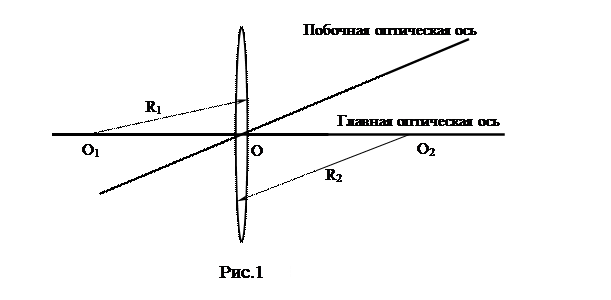Прямая, проходящая через центры кривизны O1 и O2 преломляющих поверхностей, называется главной оптической осью линзы (рис.1). В случае тонких линз можно приближенно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O.
Все прямые, проходящие через оптический центр, называются побочными (вспомогательными) оптическими осями.
|
|
|
Расстояния, отсчитываемые от центра линзы по ходу луча (вправо от точки О, если источник света S находится слева), будем считать положительными, а против хода светового луча (влево от точки О) – отрицательными. Так что на рис. 1 радиус R1 > 0, а R2 < 0.
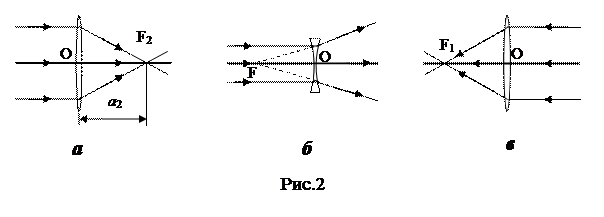
Если источник S1 находится далеко слева от собирающей линзы, т. е. пучок лучей падает на линзу параллельно главной оптической оси (рис. 2,а), то из опыта известно, что лучи пересекут оптическую ось на расстоянии а2 за линзой. Соответствующее этому случаю расстояние а2 = OF2 = f2 называется фокусным расстоянием линзы, а точка F2 – задним фокусом.
Если параллельный пучок идет справа, получим f1 = –f2, соответствующая точка F1 называется передним фокусом (рис. 2,в). Обратите внимание, что для тонкой линзы | f1| = | f2| ≡ f, если по обе стороны линзы одна и та же среда.
Если пучок после преломления получается расходящимся, то точка, где сходятся (после преломления) воображаемые продолжения лучей, падающих параллельно главной оптической оси, называют мнимым фокусом(рис. 2,б).
 |
Таким образом, фокусомлинзы называется точка, в которой после преломления собираются все лучи (или их воображаемые продолжения), падающие на линзу параллельно главной оптической оси.
Плоскости V1 и V2 (рис. 3), проходящие через фокусы перпендикулярно главной (основной) оптической оси, носят название фокальных плоскостей линзы.
Если световой пучок падает параллельно главной оптической оси, то лучи собираются в главных фокусах, если же световой пучок падает параллельно побочной оси, то лучи собираются в побочных фокусах, находящихся на фокальных плоскостях линзы (рис. 3).
Обозначим расстояние от источника света S1 до оптического центра линзы – а1, а2 – расстояние от оптического центра линзы до изображения источника (рис. 4). На чертеже а2 > 0, а а 1 < 0 и R < 0, так как эти расстояния отсчитываются влево от линзы. Проводя аналитическое решение можно показать, что расстояния а2 и а 1, связаны с радиусами кривизны линзы, находящейся в воздухе, следующим соотношением:
|
|
|
, 
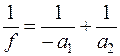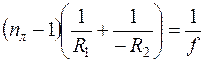, (1)
где f – фокусное расстояние линзы, т. е. расстояние от фокуса до оптического центра линзы; nл – показатель преломления материала линзы.
Данное соотношение называется формулой тонкой линзы. Из этой формулы следует, что а2 не зависит от углов β, т. е. все лучи, вышедшие из S1 под разными углами, соберутся на одном расстоянии а2 от границы раздела (в точке S2).
Это верно для лучей, исходящих из точки S1 под небольшими углами β < 10 ° (такие лучи называются параксиальными) к оптической оси, проходя линзу, лучи дважды преломляются на сферических поверхностях и собираются в одну точку S2, расположенную также на оптической оси и называемую изображением точки S1 (рис. 4).
Формулу (1) можно записать в виде:
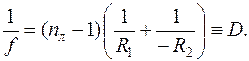(2)
Величина D носит названиеоптической силы линзыи в системе СИ измеряется в диоптриях(или м–1 ). Диоптрия равна оптической силе линзы с фокусным расстоянием в один метр. Она может быть положительной или отрицательной.
Линзы со значением D > 0 называются собирающими, так как они собирают параллельный пучок в точку, а с D < 0 – рассеивающими.
Для удобства построения хода лучей в тонких линзах на чертежах сами линзы изображают следующим образом: а – собирающая линза, б – рассеивающая (рис. 5). Рассеивающая линза имеет мнимые фокусы.
Это значит, что для нее задний фокус F2 расположен слева, а передний F1 – справа. Она образует только мнимое уменьшенное изображение.
Изображение предмета, даваемое линзой, можно получить непосредственно геометрическим построением, воспользовавшись свойством следующих лучей (рис.6):
· луч, проходящий через оптический центр линзы, не преломляется, луч (1);
· луч, падающий на линзу параллельно оптической оси после преломления, проходит через фокус, луч (2);
· луч, проходящий через передний фокус, после преломления параллелен оптической оси, луч (3).
Если от источника луч идет под некоторым углом к главной оптической оси, то необходимо построить побочную ось и найти побочный фокус, преломленный луч будет проходить через этот фокус (рис. 7).
|
|
|
Рассмотрим построение изображения в тонкой собирающей линзе (рис.6).
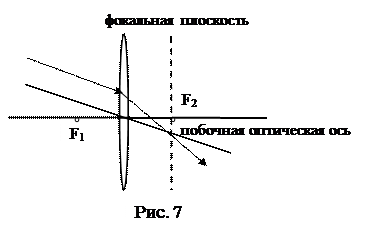
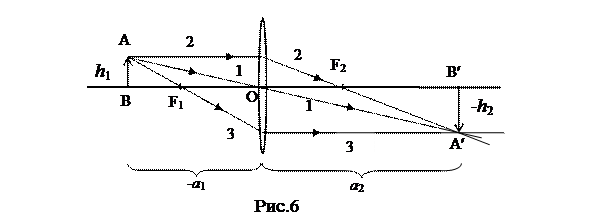При этом, если изображение формируется непосредственно преломленными лучами, оно называется действительным, а если их воображаемыми продолжениями лучей, то мнимым.
Отношение линейных размеров изображения и исходного предмета, называется линейным или поперечным увеличением β, определяется следующей зависимостью (рис.6):
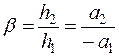. (3)
Линейное увеличение – алгебраическая величина. Оно положительно, если изображение прямое, т. е. ориентировано так же, как и сам предмет, и отрицательно, если изображение обратное.
Задания и указания к их выполнению
Задание 1. Получив от преподавателя собирающую линзу, оценить грубо ее фокусное расстояние.
Выполнение:
· по кривизне поверхностей и по показателю преломления (n= 1.5) ее фокусное расстояние, используя формулу (1).
Задание 2. Определение фокусного расстояния собирающей линзы с помощью параллельного пучка.
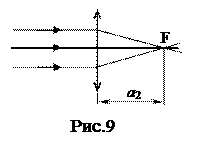Помещая собирающую линзу в параллельный пучок света, можно собрать лучи в точке, находящейся в фокусе линзы (рис. 9). Расстояние от экрана до линзы в этом случае равно фокусному расстоянию: f = a2 ..
Выполнение:
· Собрать оптическую систему.
· Отцентрировать систему (центрированная система, это система у которой центры кривизны всех сферических преломляющих и отражающих поверхностей расположены на одной прямой, называемой главной оптической осью).
· Получить параллельный пучок света.
Параллельный пучок света получают от специального устройства – коллиматора. На экране видно световое пятно, диаметр которого равен диаметру параллельного пучка света.
Параллельность пучка можно проверить, наблюдая диаметр пятна при перемещении экрана. Если диаметр пятна остается постоянным по мере продвижения экрана по скамье, то получен параллельный пучок света.
· Поместите в параллельный пучок исследуемую линзу и определите фокусное расстояние.
Задание 3. Измерить фокусное расстояние собирающей линзы методом Бесселя.
Метод Бесселя заключается в следующем. Пусть расстояние между предметом и экраном L > 4 f, при этом существуют два разных положения линзы, при которых на экране получаются четкие изображения предмета (в одном случае уменьшенное, а в другом – увеличенное (рис. 10)). Найдем эти положения из уравнения (1) и условия
|
|
|
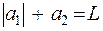(4)
Для этого выразим a2 через | a1 | и L и подставим в (1).
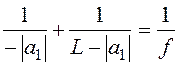. (5)
Решим данное уравнение относительно | a 1 |:
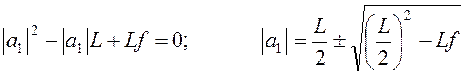. (6)
Если L > 4 f, получаются два вещественных корня. Это и значит, что, двигая линзу, можно найти два симметричных положения | a 1 | и | a 1 |¢ на расстоянии X друг от друга, когда получаются четкие изображения, один раз увеличенное, другой раз уменьшенное:
; 
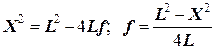, (7)
где L – расстояние между предметом и экраном; Х – расстояние между двумя положениями линзы (для увеличенного и уменьшенного изображения предмета); f – фокусное расстояние линзы.
Из этой формулы, измерив L и Х, можно найти f.
Выполнение:
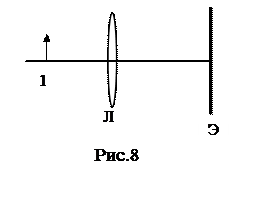
· Разместите на оптической скамье осветитель, объект, исследуемую линзу, экран. Установите расстояние между предметом и экраном L > 4 f
· Отцентрируйте оптическую систему.
· Не изменяя L, а только передвигаялинзу, получите отчетливые изображения предмета сначала увеличенного (отметьте положение линзы по шкале – Х1), затем уменьшенного (отметьте положение линзы по шкале – Х 2) (рис. 10).
· Вычислите значения Х = |Х2 – Х1|. По значениям Х и L определите фокусное расстояние по формуле (7).
· Повторите измерения для другого L и так три раза.
Задание 4. Определение фокусного расстояния рассеивающей линзы с помощью параллельного пучка.
Помещая в параллельный пучок рассеивающую линзу, получим расходящийся пучок света (рис. 11). Тогда фокусное расстояние может быть определено по формуле:
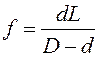, (8)
где L – расстояние от линзы до экрана; d – диаметр параллельного пучка на экране; D – диаметр пучка, после прохождения рассеивающей линзы.
Выполнение:
· Отцентрируйте оптическую систему.
· Получите параллельный пучок света (смотрите задание 3).
· Измерьте диаметр параллельного пучка d.
· Разместите на пути светового пучка исследуемую линзу, экран.
· Измерьте диаметр расширенного пучка D.
· Измерьте расстояние от линзы до экрана L.
· По значениям d, D и L определите f по формуле (8)
· Повторите измерения для других L.
· Произведите расчет ошибки измерения (см. приложение 1).
· Сопоставьте погрешности использованных методов определения фокусного расстояния.
Контрольная карточка № 1.
1. При каких условиях собирающая линза дает мнимое изображение?
2. Почему мнимое изображение нельзя получить на экране?
3. Как меняется величина изображения при удалении предмета от собирающей (рассеивающей) линзы?
|
|
|
4. Линза с фокусным расстоянием 16 см дает резкое изображение предмета при двух положениях, расстояние между которыми 60 см. Найти расстояние от предмета до экрана.
5. Определить фокусное расстояние линзы и вид линзы, если R1 = +20 см; R 2= –10 см
Контрольная карточка № 2.
1. Как изменится оптическая сила тонкой линзы, если ее поместить в воду?
2. Почему в опытах в качестве объекта нельзя использовать нить лампы?
3. Линза с фокусным расстоянием f = 16 см дает резкое изображение предмета при двух положениях, расстояние между которыми d = 6 см. Найти расстояние а1+а2 от предмета до экрана.
4. Радиусы кривизны поверхностей двояковыпуклой линзы равны R 1 = R 2 = 50 см. Показатель преломления материала линзы равен n = 1,5. Найти оптическую силу линзы.
5. Определить фокусное расстояние линзы и вид линзы, если R 1 = –10 см; R 2 = +20 см.
Контрольная карточка № 3.
1. Для каких целей используется микроскоп и зрительная труба?
2. Каков принцип работы глаза как оптического устройства? Что называется аккомодацией глаза?
3. Найти фокусное расстояние линзы, погруженной в воду, если ее фокусное расстояние в воздухе 20 см. Показатель преломления материала линзы 1,6.
4. Как изменятся фокусные расстояния и оптические силы двояковыпуклой стеклянной линзы с радиусами кривизны R1 и R2, если погрузить их в среду с показателем преломления n2.
5. Определить фокусное расстояние линзы и вид линзы, если R1 = –10 см; R 2 = ∞.
Контрольная карточка № 4.
1. Нарисуйте ход лучей в микроскопе.
2. Как изменятся фокусные расстояния и оптические силы двояковогнутой стеклянной линзы с радиусами кривизны R1 и R2, если погрузить их в среду с показателем преломления n2.
3. Предмет расположен на расстоянии a = 5 от линзы с фокусным расстоянием f =10см. На каком расстоянии b от линзы будет получено изображение? Чему при этом равно линейное увеличение? Каким будет изображение: прямым или обратным, действительным или мнимым?
4. Определить фокусное расстояние линзы и вид линзы, если R1 = ∞; R 2 = +10 см.
5. Плоско-выпуклая линза с радиусом кривизны 30 см и показателем преломления 1,5 дает изображение предмета с увеличением, равным 2. Найти расстояние предмета и изображения от линзы. Построить чертеж.
|
|
|
