Вычисление сингулярного разложения

Применение сингулярной матрицы в химии

(Реферат)

 

 

О Г Л А В Л Е Н И Е

Введение. 3

Глава 1. Общие сведения о сингулярном разложении и сингулярных матрицах 4

1.1. Ортогональное разложение посредством сингулярного разложения. 4

1.2. Вычисление сингулярного разложения. 5

Глава 2. Применение сингулярных матриц при многомерном анализе химических данных факторными методами. 7

2.1. Общие сведения о факторных методах. 7

2.2. Операции с матрицами и многомерный анализ данных. 9

2.3. Свойства сингулярной матрицы.. 10

Заключение. 12

Список используемой литературы.. 16

 

 

Введение

 

Как известно, химия часто оказывается на перекрестке разных дисциплин. Для химика всегда есть большой соблазн в том, чтобы заняться какой-то чрезвычайно узкой областью, где он останется защищенным от всех превратностей, наслаждаясь удобством положения единст­венного в своем роде специалиста. Чтобы постоянно быть в курсе дела и в готовности встретить любую новую ситуацию, химику требуется быть знако­мым с огромным объемом информации, необходимой не только для движения вперед, но и просто для сохранения своего положения.

При написании данного реферата была использована следующая литература, содержащая информацию о сингулярных матрицах и применении их в химии:

· книга «ЭВМ помогает химии» (пер. с англ) под ред. Г. Вернена, М. Шанона, в которой рассмотрено применение ЭВМ в различных областях химии: синтез органических соединений, кристаллография, масс-спектрометрия и т. д.

· книга Ч.Лоусона и Р.Хенсона «Численное решение задач метода наименьших квадратов» (пер. с англ), посвященная изложению численных решений линейных задач метода наимень­ших квадратов.

 

Глава 1. Общие сведения о сингулярном разложении и сингулярных матрицах

Ортогональное разложение посредством сингулярного разложения

 

В этом пункте данного реферата будет описано одно практически полезное ортогональ­ное разложение т x n - матрицы А. Мы покажем здесь, что невырожденную под­матрицу R матрицы A можно еще более упростить так, чтобы она стала невырожден­ной диагональной матрицей. Получаемое в результате разложение особенно полезно при анализе влияния ошибок входной информации на решение задачи НК.

Это разложение тесно связано со спектральным разложением симметрич­ных неотрицательно определенных матриц A^TA и AA^T.

 

Теорема (сингулярное разложение). Пусть А - m x n -матрица ранга k. Тогда существуют ортогональная m x m матрица U, ортогональ­ная n x n -матрица V и диагональная m x n -матрица S) такие, что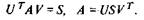

Матрицу S можно выбрать так, чтобы ее диагональные элементы составля­ли невозрастающую последовательность; все эти элементы неотрицательны и ровно k из них строго положительны.

Диагональные элементы S называются сингулярными числами А.

Доказательства данной теоремы приводить не имеет смысла во избежание нагромождения множества сложных математических выкладок, прямого отношения к теме, рассматриваемой в данном реферате, не имеющих. Ограничимся следующим численным примером, в котором дано сингулярное разложение матри­цы А вида:

 

Вычисление сингулярного разложения

Рассмотрим теперь построение сингулярного разложения т Х n - матрицы в предположении, что т > п. Сингулярное разложение будет вычислено в два этапа.

На первом этапе А преобразуется к верхней двухдиагональной матрице  посредством последовательности (не более чем из n — 1) преобразований Хаусхолдера

 

где

 

Трансформирующая матрица выбирается так, чтобы аннулировать элементы i + 1,..., т столбца i; матрица Hi — так, чтобы аннулировав элементы i + 1,.... п строки / - 1.

Заметим, что Q_n - это попросту единичная матрица. Она включена, чтобы упростить обозначения; Q_n также будет единичной матрицей при от = я, но при т > п она, вообще говоря, отличается от единичной.

Второй этап процесса состоит в применении специальным образом адап­тированного QR-алгоритма к вычислению сингулярного разложения матрицы  

Здесь 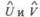- ортогональные матрицы, a S диагональная.

 

Можно получить сингулярное разложение А:

Сингулярное разложение  матрицы В будет получено посредством следующего итерационного процесса:

Здесь  - ортогональные матрицы, а  B_k - верхняя двухдиагональ­ная матрица для всех k.

Заметим, что диагональные элементы матрицы  полученной непосред­ственно из этой итерационной процедуры, не являются в общем случае ни положительными, ни упорядоченными. Эти свойства обеспечиваются специальной последующей обработкой.

Сама итерационная процедура представляет собой (QR-алгоритм Фрэнсиса, адаптированный Голубом и Райншем к задаче вычисления сингулярных чисел.

12	Поделиться:

Воспользуйтесь поиском по сайту: