 |
Внизу: Моя формула и открытие для расчета расхождений СРЕДНЕГО ПОЛЯ и сходимости идеализированного магнита. Открытие авторских прав 28.07.2014 Кен Л. Уиллер
|
|
|
|
Внизу: Хотя взаимная квадрополярная дивергенция-конвергенция в целом необходима, поскольку обе они существуют на любом полюсе, необходимо понимать, что магнетизм не является движущей силой магнетизма или представляет собой расходящиеся и сходящиеся погодные модели движения воздуха, управляемые движением воздуха. В случае Земли это постоянный нагрев и охлаждение в результате ежедневных дневных и ночных циклов нагрева и охлаждения, как и в случае с предполагаемым «магнитом», который приводится в действие когерентной диэлектрической инерцией, которая при разряде требует расходящегося магнетизма и сходящегося магнитного поля. -интеграция, или диэлектрическая пустота.
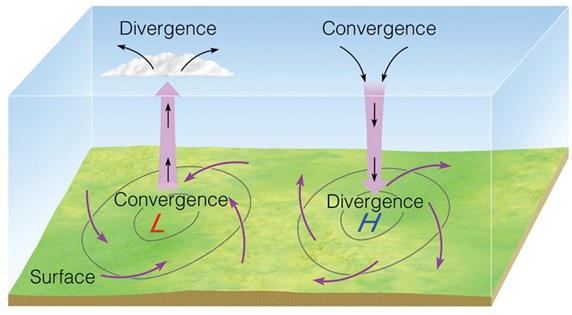
Внизу: Каждый полюс каждого магнита имеет зону центробежного расходящегося антициклонического давления и зону центростремительного вакуума циклонического давления. Саморегуляция давления поля является Эфирной точкой опоры инерции, внутри которой разрядка вызывает создание результирующего магнитным полям пространства, а это дополнительно вызывает потерю инерции и циклическую разрядку.
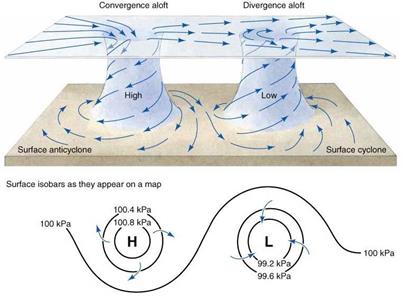
Внизу: Слева мы можем представить диэлектрическую инерционную плоскость каждого «магнита», внутри которого магнитное торможение индуцирует вечный контур магнитного расхождения, на который питается разряд, и цикл повторяется бесконечно. «Магнит» — это буквально вечный вид обратной связи магнито-диэлектрической саморегулирующейся гармонии и взаимного совершенства давления поля.
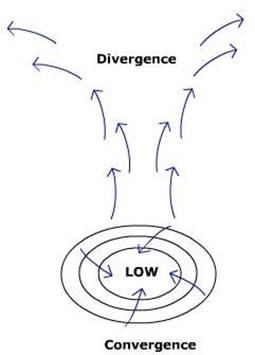

Ниже: если вы можете понять, как посредничество давления работает в эмпирических моделях, вы можете понять то же самое в эфирных модальностях. Дивергенция влечет за собой конвергенцию, и, в отличие от других явлений природы, поля не могут заканчиваться в пространстве, а только на самих себе или аффективно на другом поле. Точно так же всякая полярность есть излучение, и в единой системе связи обратная относительная полярность спина не только всегда наблюдается, но абсолютно необходима без исключения.
|
|
|


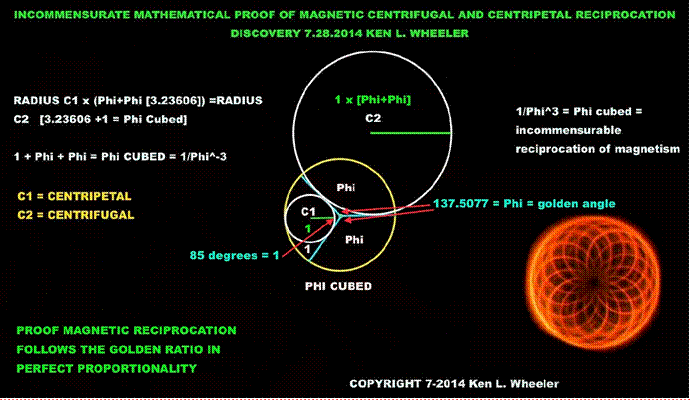
Доказательство того, что магнитные центробежные и центростремительные возвратно-поступательные движения следуют золотому сечению и представляют собой системный гиперболоид Фи в кубе.
Математика магнитного вихря — это всего лишь расширяющаяся и сжимающаяся переплетающаяся сингулярная система диэлектрического гиперболоида, составленная из расходящегося поляризованного (очевидно так и по определению необходимого) излучения и сходящихся диэлектрических пустот в центростремительной точке обоих поляризованных пространственных расхождений («полюсов»). Наинизшее возможное опосредование давления, вызванное модальностями противоположного поля, расходящимся и сходящимся, а также прецессией гиромагнитного давления, может быть выражено только с помощью фи и диэлектрического гиперболоида.
Внизу: Моя формула и открытие для расчета расхождений СРЕДНЕГО ПОЛЯ и сходимости идеализированного магнита. Открытие авторских прав 28. 07. 2014 Кен Л. Уиллер

Внизу: Математическое доказательство того, что центростремительные сжимающие поля «вытягивают» сходящиеся сферы вихре-тороида, а центробежные поля «вытягивают» расширяющиеся расходящиеся вихре-тороидальные гиперболоидные сферы. Это соотношение дивергенции и конвергенции золотого сечения равно сходящимся центростремительным полям = центростремительный радиус 1; и центробежные расходящиеся поля являютсярадиус центростремительного значения 1, умноженный на (Phi+Phi [3, 23606]). Или: (радиус C1 x 3, 23606 = радиус C2), что вместе = куб Phi (C1r+Phi+Phi = 4, 23606). Фи в круге = золотой угол 137, 5077 градусов. 1 в круге = радиус C1, который составляет 85 градусов. Открытие авторских прав 28. 07. 2014 Кен Л. Уилер
|
|
|
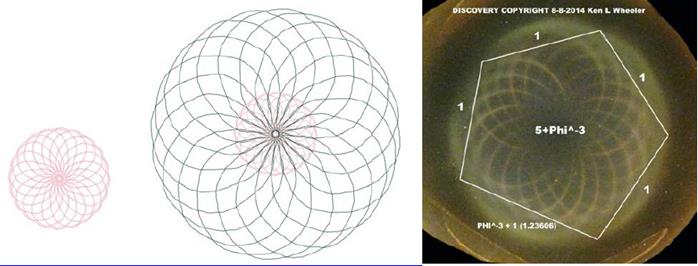
Внизу: экстраполированный сходящийся магнетизм, а в середине сходящийся и расходящийся магнетизм. Справа известное, но эмпирически продемонстрированное открытие несоизмеримости поля 5+Phi^-3. Открытие авторских прав 8-8-2014 Кен Л. Уилер
|
|
|


