 |
Особенности тестирования «белого ящика»
|
|
|
|
Обычно тестирование «белого ящика» основано на анализе управляющей структуры программы [2], [13]. Программа считается полностью проверенной, если проведено исчерпывающее тестирование маршрутов (путей) ее графа управления.
В этом случае формируются тестовые варианты, в которых:
q гарантируется проверка всех независимых маршрутов программы;
q проходятся ветви True, False для всех логических решений;
q выполняются все циклы (в пределах их границ и диапазонов);
q анализируется правильность внутренних структур данных.
Недостатки тестирования «белого ящика»:
1. Количество независимых маршрутов может быть очень велико. Например, если цикл в программе выполняется k раз, а внутри цикла имеется п ветвлений, то количество маршрутов вычисляется по формуле
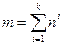 .
.
При п = 5 и k = 20 количество маршрутов т = 1014. Примем, что на разработку, выполнение и оценку теста по одному маршруту расходуется 1 мс. Тогда при работе 24 часа в сутки 365 дней в году на тестирование уйдет 3170 лет.
2. Исчерпывающее тестирование маршрутов не гарантирует соответствия программы исходным требованиям к ней.
3. В программе могут быть пропущены некоторые маршруты.
4. Нельзя обнаружить ошибки, появление которых зависит от обрабатываемых данных (это ошибки, обусловленные выражениями типа if abs (a-b) < eps..., if(a+b+c)/3=a...).
Достоинства тестирования «белого ящика» связаны с тем, что принцип «белого ящика» позволяет учесть особенности программных ошибок:
1. Количество ошибок минимально в «центре» и максимально на «периферии» программы.
2. Предварительные предположения о вероятности потока управления или данных в программе часто бывают некорректны. В результате типовым может стать маршрут, модель вычислений по которому проработана слабо.
|
|
|
3. При записи алгоритма ПО в виде текста на языке программирования возможно внесение типовых ошибок трансляции (синтаксических и семантических).
4. Некоторые результаты в программе зависят не от исходных данных, а от внутренних состояний программы.
Каждая из этих причин является аргументом для проведения тестирования по принципу «белого ящика». Тесты «черного ящика» не смогут реагировать на ошибки таких типов.
Способ тестирования базового пути
Тестирование базового пути — это способ, который основан на принципе «белого ящика». Автор этого способа — Том МакКейб (1976) [49].
Способ тестирования базового пути дает возможность:
q получить оценку комплексной сложности программы;
q использовать эту оценку для определения необходимого количества тестовых вариантов.
Тестовые варианты разрабатываются для проверки базового множества путей (маршрутов) в программе. Они гарантируют однократное выполнение каждого оператора программы при тестировании.
Потоковый граф
Для представления программы используется потоковый граф. Перечислим его особенности.
1. Граф строится отображением управляющей структуры программы. В ходе отображения закрывающие скобки условных операторов и операторов циклов (end if; end loop) рассматриваются как отдельные (фиктивные) операторы.
2. Узлы (вершины) потокового графа соответствуют линейным участкам программы, включают один или несколько операторов программы.
3. Дуги потокового графа отображают поток управления в программе (передачи управления между операторами). Дуга — это ориентированное ребро.
4. Различают операторные и предикатные узлы. Из операторного узла выходит одна дуга, а из предикатного — две дуги.
4. Предикатные узлы соответствуют простым условиям в программе. Составное условие программы отображается в несколько предикатных узлов. Составным называют условие, в котором используется одна или несколько булевых операций (OR, AND).
|
|
|
5. Например, фрагмент программы
if a OR b
then x
else у
end if;
вместо прямого отображения в потоковый граф вида, показанного на рис. 6.4, отображается в преобразованный потоковый граф (рис. 6.5).
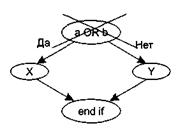
Рис. 6.4. Прямое отображение в потоковый граф

Рис. 6.5. Преобразованный потоковый граф
6. Замкнутые области, образованные дугами и узлами, называют регионами.
7. Окружающая граф среда рассматривается как дополнительный регион. Например, показанный здесь граф имеет три региона — Rl, R2, R3.
Пример 1. Рассмотрим процедуру сжатия:
процедура сжатие
1 выполнять пока нет EOF
1 читать запись;
2 если запись пуста
3 то удалить запись:
4 иначе если поле а >= поля b
5 то удалить b;
6иначе удалить а;
7а конец если;
7а конец если;
7b конец выполнять;
8 конец сжатие;

Рис. 6.6. Преобразованный потоковый граф процедуры сжатия
Она отображается в потоковый граф, представленный на рис. 6.6. Видим, что этот потоковый граф имеет четыре региона.
Цикломатическая сложность
Цикломатическая сложность — метрика ПО, которая обеспечивает количественную оценку логической сложности программы. В способе тестирования базового пути Цикломатическая сложность определяет:
q количество независимых путей в базовом множестве программы;
q верхнюю оценку количества тестов, которое гарантирует однократное выполнение всех операторов.
Независимым называется любой путь, который вводит новый оператор обработки или новое условие. В терминах потокового графа независимый путь должен содержать дугу, не входящую в ранее определенные пути.
ПРИМЕЧАНИЕ
Путь начинается в начальном узле, а заканчивается в конечном узле графа. Независимые пути формируются в порядке от самого короткого к самому длинному.
Перечислим независимые пути для потокового графа из примера 1:
Путь 1: 1-8.
Путь 2: 1-2-3-7а-7b-1-8.
Путь 3: 1-2-4-5-7а-7b-1-8.
Путь 4: 1-2-4-6-7а-7b-1-8.
Заметим, что каждый новый путь включает новую дугу.
Все независимые пути графа образуют базовое множество.
Свойства базового множества:
1) тесты, обеспечивающие его проверку, гарантируют:
q однократное выполнение каждого оператора;
|
|
|
q выполнение каждого условия по True-ветви и по False-ветви;
2) мощность базового множества равна цикломатической сложности потокового графа.
Значение 2-го свойства трудно переоценить — оно дает априорную оценку количества независимых путей, которое имеет смысл искать в графе.
Цикломатическая сложность вычисляется одним из трех способов:
1) цикломатическая сложность равна количеству регионов потокового графа;
2) цикломатическая сложность определяется по формуле
V(G)-E-N+2,
где Е — количество дуг, N — количество узлов потокового графа;
3) цикломатическая сложность формируется по выражению V(G) =p+ 1, где р — количество предикатных узлов в потоковом графе G.
Вычислим цикломатическую сложность графа из примера 1 каждым из трех способов:
1) потоковый граф имеет 4 региона;
2) V(G) = 11 дуг - 9 узлов + 2 = 4;
3) V(G) = 3 предикатных узла +1=4.
Таким образом, цикломатическая сложность потокового графа из примера 1 равна четырем.
|
|
|


