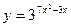|
Балльно-рейтинговая карта дисциплины
|
|
|
|
ПОВОЛЖСКАЯ ГОСУДАРСТВЕННАЯ СОЦИАЛЬНО-ГУМАНИТАРНАЯ АКАДЕМИЯ
Кафедра математики и методики обучения
Утверждено
на заседании кафедры
Протокол №
«» ____________ 2012 г.
Балльно-рейтинговая карта дисциплины
«Математический анализ»
Факультет математики, физики и информатики. Специальность – «Математика».
Курс 1 Семестр 2
Ведущий преподаватель:
к.ф.-м.н., доцент Барова Е.А.
Самара, 2012
| Вид контроля | Минимальное количество баллов | Максимальное количество баллов | |
| Модуль 1. Дифференциальное исчисление | |||
| Текущий контроль по модулю: | |||
| Аудиторная работа: | |||
| Самостоятельная работа № 1 «Таблица производных» | |||
| Самостоятельная работа № 2 «Производные функций, заданных параметрически и неявно» | |||
| Самостоятельная работа (специальные формы на выбор студента) – доклад на одну из предложенных тем | |||
| Контрольное мероприятие по модулю: | |||
| Теоретическая часть (коллоквиум) | |||
| Практическая часть (контрольная работа) | |||
| Промежуточный контроль | |||
| Модуль 2. Применение производных к исследованию функций | |||
| Текущий контроль по модулю: | |||
| Аудиторная работа: | |||
| Самостоятельная работа № 1 «Наибольшее и наименьшее значения функции» | |||
| Самостоятельная работа (специальные формы на выбор студента) – доклад на одну из предложенных тем | |||
| Контрольное мероприятие по модулю – индивидуальная работа «Исследование функций и построение их графиков» | |||
| Промежуточный контроль | |||
| Промежуточная аттестация |
Преподаватель Барова Е.А., к.ф.-м.н., доцент кафедры математики и методики обучения
|
|
|
| Вид контроля | Примеры заданий, критерии оценки и количество баллов | Темы для изучения и образовательные результаты | ||||||||||||||||
| Модуль 1. Дифференциальное исчисление | ||||||||||||||||||
| Аудиторная работа | ||||||||||||||||||
| Самостоятельная работа № 1 «Таблица производных» | Примеры заданий.Уметь вычислять производные элементарных и сложных функций. Например:
Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. | Понятие производной. Вывод формул производных основных элементарных функций. Таблица производных. Теоремы о производных суммы, разности, произведения, частного. Производная сложной функций. | ||||||||||||||||
| Самостоятельная работа № 2 «Производные функций, заданных параметрически и неявно» | Примеры заданий.Уметь находить производные функций, заданных неявно и параметрически. Например,
1. Найти производную показательно-степенной функции  .
2. Найти производную первого порядка .
2. Найти производную первого порядка  и второго порядка и второго порядка  от функции, заданной параметрически от функции, заданной параметрически
 Критерий оценки:
2 балла – пример решен правильно,
1 балл – пример решен с незначительными ошибками,
0 баллов – пример не решен.
Критерий оценки:
2 балла – пример решен правильно,
1 балл – пример решен с незначительными ошибками,
0 баллов – пример не решен.
| Теоремы о производных суммы, разности, произведения, частного. Производная сложной функций. Производные высших порядков. Производные функций, заданных параметрически и неявно. | ||||||||||||||||
| Самостоятельная работа (специальные формы на выбор студента) – доклад на одну из предложенных тем | Примеры тем.
1. Геометрический и физический смысл производной.
2. Дифференцирование обратной функции.
3. Односторонние производные.
4. Механический смысл производной второго порядка.
5. Касательная и нормаль.
6. Производные второго порядка от неявных функций.
7. Теорема Ферма.
8. Теорема Роля.
9. Теорема Лагранжа.
Критерий оценки:
| |||||||||||||||||
| Контрольное мероприятие по модулю | ||||||||||||||||||
| Теоретическая часть (коллоквиум) | Перечень вопросов.
1. Задачи, приводящие к понятию производной (о скорости, о касательной). Понятие производной функции.
2. Теорема о связи дифференцируемости с непрерывностью.
3. Правила дифференцирования. Доказать, что  , ,  , ,  , ,  .
4. Теорема о производной суммы, произведения и частного.
5. Производная сложной функции. Теорема о производной сложной функции.
6. Таблица производных сложной функции.
7. Производные высших порядков.
8. Производная показательно-степенной функции.
9. Производная функции, заданной параметрически. Теорема о производной функции, заданной параметрически. Производная второго порядка.
10. Пример функции, непрерывной, но не дифференцируемой в точке.
11. Правило Лопиталя.
Критерий оценивания. .
4. Теорема о производной суммы, произведения и частного.
5. Производная сложной функции. Теорема о производной сложной функции.
6. Таблица производных сложной функции.
7. Производные высших порядков.
8. Производная показательно-степенной функции.
9. Производная функции, заданной параметрически. Теорема о производной функции, заданной параметрически. Производная второго порядка.
10. Пример функции, непрерывной, но не дифференцируемой в точке.
11. Правило Лопиталя.
Критерий оценивания.
| |||||||||||||||||
| Практическая часть (контрольная работа) | Примеры заданий.Найти  : :
|
Критерий оценивания.
| Баллы | Критерии |
| 27-30 | Выполнены правильно все задания. Возможны одна-две негрубые ошибки. |
| 22-26 | Выполнено правильно 70% работы. Более высокий балл достигается выполнением работы над ошибками и частичным переписыванием задач контрольной работы по выбору преподавателя. |
| 15-21 | Выполнено правильно 50 % работы. Выполнена работа над ошибками. Более высокий балл достигается частичным переписыванием задач контрольной работы по выбору преподавателя. |
| 9-14 | Выполнено правильно 30 % работы. Выполнена работа над ошибками. Более высокий балл достигается полным переписыванием работы. |
| 0-8 | Выполнено правильно менее 30 % работы. Выполнена работа над ошибками. Работа требует обязательного переписывания. Переписанная работа оценивается как вновь сданная. |
|
|
|
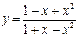 на
на  .
Критерий оценки:
3-4 балла – пример решен правильно, допущены мелкие неточности, не влияющие на верный ответ;
1-2 балла – ход решения примера изложен верно, допущены ошибки, влияющие на верный ответ;
0 баллов – пример не решен.
.
Критерий оценки:
3-4 балла – пример решен правильно, допущены мелкие неточности, не влияющие на верный ответ;
1-2 балла – ход решения примера изложен верно, допущены ошибки, влияющие на верный ответ;
0 баллов – пример не решен.
 ,
,  ,
,  ,
,  .
2. Исследование функций, заданных параметрически.
3. Исследование функций, заданных неявно.
4. Дифференциалы высших порядков.
5. Применение дифференциала к приближённым вычислениям.
6. Наибольшее и наименьшее значения функции в текстовых задачах.
Критерий оценки:
.
2. Исследование функций, заданных параметрически.
3. Исследование функций, заданных неявно.
4. Дифференциалы высших порядков.
5. Применение дифференциала к приближённым вычислениям.
6. Наибольшее и наименьшее значения функции в текстовых задачах.
Критерий оценки:
| Балл | Критерии |
| Представлен реферат без презентации. | |
| 3) Представлен реферат. 4) Представлена презентация реферата. | |
| 4) Представлен реферат. 5) Представлена презентация реферата. 6) Сделан доклад по теме реферата. |
|
|
|
 ,
,  ,
,  .
Критерий оценки. Исследование каждой функции оценивается в 14 баллов.
.
Критерий оценки. Исследование каждой функции оценивается в 14 баллов.
| Баллы | Критерии |
| 11-14 | Все исследования проведены верно. Возможно несколько негрубых ошибок, сильно не влияющих на исследование и исправляемых в ходе беседы с преподавателем |
| 8-10 | Проведено правильно более 50% исследования функции. Остальные задания выполнены после собеседования, совместно с преподавателем. Если студент, после собеседования по контрольной работе с преподавателем, выполнил нерешенные задания самостоятельно, то балл повышается. |
| 4-7 | Проведено правильно от 30 % до 50 % исследования функции. После собеседования с преподавателем студент обязательно выполняет оставшиеся задания. Если студент выполняет эти задания самостоятельно, то работа оценивается как первоначально сданная. |
| 0-3 | Выполнено правильно менее 30 % исследований. Работа возвращается на доработку. |


 ;
2.
;
2.  ;
3.
;
3.  ;
4.
;
4.  ;
5.
;
5.  ;
6.
;
6.  ;
7.
;
7.  ;
8.
;
8.  ;
9.
;
9. 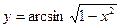 ;
;
 ;
11.
;
11.  ;
12.
;
12.  ;
13.
;
13.  ;
14.
;
14.  ;
15.
;
15.  16.
16.  ;
17.
;
17.  ;
18.
;
18.  .
.