Бесконечно малые и бесконечно большие функции

Глава II. ПРЕДЕЛ ФУНКЦИИ

Понятие предела функции

Пусть функция f(x) определена в некоторой окрестности точки x₀ за исключением быть может самой точки x₀.

Определение 1. Число А называется пределом функции f(x) в точке x=x₀, если для любого e>0 существует число d>0 такое, что для всех x, удовлетворяющих условию , x¹x₀, имеет место неравенство <e. При этом пишут

.

Согласно данному определению справедливы следующие утверждения:

1. Предел постоянной величины С в точке x=x₀равен значению этой постоянной, т.е.

.

2. Функция f(x)=х в точке x=x₀имеет предел, равный x₀, т.е.

.

Свойства пределов

Теорема 1. Если существуют пределы функций f(x) и g(x) при x®x₀, то существуют пределы суммы (разности), произведения и, при условии , частного этих функций, т.е.

1) ;

2) ;

3) = , .

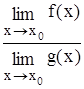Замечание. Теорема верна также и в случае, когда x_{0 =} ¥, +¥, -¥.

Следствия

1⁰. Постоянный множитель может быть вынесен за знак предела

= С × , С = const.

2⁰. Если nÎN, то

= , = .

3⁰. Предел степени равен степени предела

= , nÎN.

4⁰. Предел многочлена P(x) при x®x₀равен значению этого многочлена при x=x₀

= P(x₀).

5⁰. Предел дробно-рациональной функции при x®x₀равен значению этой функции при x=x₀, если Q(x₀)¹0

= .

Пример 1. Вычислить .

Решение. На основании п.п. 1, 2 Теоремы 1 имеем:

= =

= 2 × 1 × 1 + 1 - 3 = 0.

При решении данного примера можно непосредственно воспользоваться следствием Теоремы 1 о пределе многочлена.

= 2 × 1²+ 1 - 3 = 0.

Пример 2. Вычислить .

Решение. Так как = 4 - 3 = 1 ¹ 0, то применимо следствие 5⁰ Теоремы 1 о пределе дробно-рациональной функции

= 8.

 

Односторонние пределы

Определение 2. Число А называется левым пределом функции f(x) в точке х=х₀, если для любого e>0 существует число d>0 такое, что для всех x, удовлетворяющих условиям <d, x < x₀, имеет место неравенство <e. При этом пишут

(x® x₀-0 означает стремление х к х₀ слева).

Определение 3. Число В называется правым пределом функции f(x) в точке x=x₀, если для любого e>0 существует число d>0 такое, что для всех x, удовлетворяющих условиям < d, x > x₀, имеет место неравенство < e. При этом пишут

(x®x₀+0 означает стремление x к x₀ справа).

Замечание. Для существования предела функции f(x) в точке x=x₀ необходимо и достаточно, чтобы выполнялось равенство

, т.е. А = B.

 

Непрерывность функции. Точки разрыва

Определение 4. Функция f(x) называется непрерывной в точке x=x₀, если она определена в некоторой окрестности точки x₀, существует предел функции при x®x₀ и он равен значению функции в этой точке

.

Так как , то условие непрерывности функции в точке x₀ может быть записано в виде .

Следствиями этой формулы являются выражения:

,

= .

Пример 3. Вычислить .

Решение. Так как функции ln(x-1) и непрерывные в точке x=2, то в соответствии с Теоремой 1 и определением непрерывной функции имеем

= + =

= ln(2 - 1) + = 0 + 1 = 1.

Теорема 2. Пусть функции f(x) и g(x) непрерывны в точке x=x₀. Тогда функции f(x) ± g(x), f(x) × g(x) и, при условии g(x) ¹ 0, f(x) / g(x) также непрерывны в этой точке.

Пример 4. Вычислить .

Решение. При x = p знаменатель дроби отличен от нуля. Кроме того, функции 1, sin x и ln непрерывны в этой точке. Тогда в соответствии с Теоремой 2 функция также непрерывна в точке x = p, т.е. предел функции и ее значение в этой точке равны.

Переходя к пределу, получим:

= = = 1.

Определение 5. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Различают два вида точек разрыва.

Определение 6. Точка x₀ называется точкой разрыва первого рода функции f(x), если в ней функция имеет конечные односторонние пределы.

Определение 7. Точка x₀ называется точкой разрыва второго рода функции f(x), если хотя бы один из односторонних пределов в этой точке равен -¥ или +¥.

Бесконечно малые и бесконечно большие функции

Определение 8. Функция a(x) называется бесконечно малой при x®х₀, если .

Пусть a(х) и b(х) – две бесконечно малые функции при x®x₀. Тогда:

1) если = 0, то a(x) называется бесконечно малой более высокого порядка, чем b(x);

2) если ¹ 0 (А - число), то a(x) и b(x) называются бесконечно малыми одного порядка;

3) если , то a(x) и b(x) называются эквивалентными бесконечно малыми (a(x)~b(x) при x®x₀).

Определение 9. Функция f(x) называется бесконечно большой при х®x0, если для любого М>0 найдется такое d>0, что для любых х (x ¹ x0), удовлетворяющих условию , следует . При этом пишут .

Выражения +¥ и -¥ означают соответственно, что f(x) > M и f(x) < -M при , x ¹ x0.

Поделиться:

Воспользуйтесь поиском по сайту: