Формула Кардано в современной математической модели. Один из корней уравнения.

Квадрат Кардано.

Чтобы не нарушать собственное предвидение, согласно легенде он покончил собой в отведенном им срок со словами: «Если и неверно, то не плохо придумано». Перед смертью, находясь в религиозном экстазе, Кардано сжег свои книги, усмотрев в них противоречие «с волей Божьей».

Предложенный Кардано «шифр-решетка» лежит в основе знаменитого «шифра Решелья», в котором шифрованный текст внешне имел вид «невинного послания». Из плотного материала вырезался прямоугольник размером, например 7*10; в нем проделывались окна (на рисунке они заштрихованы).

О	Т	К	Р	Ы	Й		К	О	Д
Ш	И	Ф	Р	О	В	А	Н	И	Е
Н	А		К	А	Ж	Д	О	Г	О
Т	Е	О	Р	И	Я		А	Д	А
Т	О	П	О	Г	Р	А	Ф	И	Я
Л	И	Б	Е	Р	А	Л	И	З	М
И	Н	Ф	О	Р	М	А	Ц	И	Я

 

Секретный текст вписывался в эти окна, затем решетка снималась и оставшиеся клетки заполнялись так, чтобы получилось: «КВАДРАТ ПОЛИБИЯ» с помощью решетки можно спрятать в текст с содержанием: «ОТКРЫТЫЙ ТЕКСТ. ШИФРОВАНИЕ. НА КАЖДОГО.».

Кардано принадлежит также идея поворотной решетки как средства шифрования. Изначально обычная решетка представляла собой лист из твердого материала, в котором через неправильные интервалы сделаны прямоугольные вырезы высотой для одной строчки и различной длины. Накладывая эту решетку на лист писчей бумаги, можно было записать в вырезы секретное сообщение. После этого, сняв решетку, нужно было заполнить оставшиеся свободные места на листе бумаги неким текстом, маскирующим секретное сообщение. Подобным стенографическим методом маскировки сообщения пользовались многие известные исторические лица, например кардинал Ришелье во Франции и русский дипломат, и писатель А.Грибоедов. Так, Ришелье использовал прямоугольник размера 7*10 (число строк*число столбцов). Для длинных сообщений прямоугольник использовался несколько раз. Прорези трафарета размещались в позициях:

· ШИФР ЦЕЗАРЯ

Шифр сдвига, код Цезаря или сдвиг Цезаря — самый простой и известный шифр. Так как шифр Цезаря является частным случаем шифра простой замены, то как и для всех шифров простой замены - шифрование шифром Цезаря заключается в замене символов открытого текста согласно таблице шифрования, которая для шифра Цезаря формируется следующим образом: первому символу алфавита соответствует k+1-ый символ этого же алфавита, второму - k+2-ый, третьему - k+3-ый и так далее (предпоследнему - k-1-ый, последнему символу алфавита - k-ый), где k - ключ, так например при k=3, "А" заменяется на "Г", "Б" на "Д", "В" на "Е", "Э" на "А", "Ю" на "Б", "Я" на "В". Таким образом, шифр Цезаря является частным случаем Аффинного шифра.
Так например, из предложения Светония о Цезаре " Если у него было что либо конфиденциальное для передачи, то он записывал это шифром, то есть так изменял порядок букв алфавита, что нельзя было разобрать ни одно слово. " путем шифрования шифром Цезаря получается " Зфол ц рзёс дюос ъхс олдс нсрчлжзрщлгоярсз жов тзузжгъл, хс ср кгтлфюего ахс ылчусп, хс зфхя хгн лкпзрво тсувжсн дцне гочгелхг, ъхс рзоякв дюос угксдугхя рл сжрс фосес. "

Шифр Цезаря так был назван в честь того самого Цезаря (Гая Юлия), который использовал этот шифр для секретной переписки с левым сдвигом 3 (k=3). В настоящее же время шифр Цезаря, как и все шифры простой замены, легко дешифруется и не имеет практического применения (кроме как сокрытия неконфиденциальной информации от случайного прочтения, например ответы на загадки, спойлеры, оскорбления, для английского алфавита в этих целях применяется шифр Цезаря с k=13 (называется ROT13), что делает его симметричным).

Для дешифрования (взлома) шифров простой замены обычно используется анализ частот встречаемости различных символов шифровки (для этого в приложении CryptoApp к Вашим услугам " Частотный автодешифратор "), однако если дешифровщик знает что шифровка была зашифрована шифром Цезаря, то ему достаточно перебрать все возможные ключи, благо их немного (для русского алфавита - всего 33).

· ШИФР ПЕРЕСТАНОВКИ

Приведен пример второго исторического шифра – шифр перестановки. Выберем целое положительное число, скажем, 5; расположим числа от 1 до 5 в двухстрочной записи, в которой вторая строка – произвольная перестановка чисел верхней строки:

Это конструкция носит название подстановки, а число 5 называется ее степенью.

Зашифруем фразу «СВЯЩЕННАЯ РИМСКАЯ ИМПЕРИЯ». В этой фразе 23 буквы. Дополним ее двумя произвольными буквами (например, Ь, Э) до ближайшего числа, кратного 5, то 25. Выпишем эту дополнитеьную фразу без пропусков, одновременно разбив ее на пятизначные группы:

СВЯЩЕ ННАЯР ИМСКА ЯИМПЕ РИЯЬЭ

Буквы каждой группы переставим в соответсвии с указанной двухстрочной записью по следующему правилу: первая буква встает на третье место, вторая – на второе, третья – на пятое, четвертая – на первое и пятая – на четвертое. Полученный текст выписывается без пропусков:

ЩВСЕЯЯННРАКМИАСПИЯЕМЬИРЭЯ.

При расшифровании текст разбивается на группы по 5 букв и буквы переставляются в обратном порядке: 1 на 4 место, 2 на 2, 3 на 1, 4 на 5 и 5 на 3. Ключом шифра является выбранное число 5 и порядок расположения чисел в нижнем ряду двухстрочной записи.

· КВАДРАТ ПОЛИБИЯ

Еще одно изобретение древних греков – так называемый вкадрат Полибия, (Полибий – греческий государственный деятель, полководец, историк, ІІІ век до н.э.). Применительно к современному латинскому алфавиту из 26 букв шифрование по этому квадрату заключалось в следующем. В квадрать размером 5*5 клеток выписываются все буквы алфавита, при этом буквы I, J не различаются (J отождествляется с буквой I):

	A	B	C	D	E
A	A	B	C	D	E
B	F	G	H	I	K
C	L	M	N	O	P
D	Q	R	S	T	U
E	V	W	X	Y	Z

Шифруемая буква заменялась на координаты, в котором она записана. Так, В заменялась на АВ, F на BA, R на DB и т.д. При расшифровании каждая такая пара определяла соответсвующую букву сообщения. Заметим, что секретом в данном случае является сам способ замены букв. Ключ в этой системе отсутвует, поскольку используется фиксированный алфавитный порядок следования букв.

Услажненный вариант шифра Полибия заключается в записи букв в квадрат в произвольном (неалфавитном) порядке. Этот произвольный порядок является ключом.

Здесь однако, появилась и некоторое неудобство. Произвольный порядок букв трудно запомнить, поэтому пользователю шифра было необходимо постоянно иметь при себе ключ – квадрат. Появилась опасность тайного ознакомления с ключом посторонних лиц. В качестве крмпромиссного решения был предложен ключ – пароль. Легко запоминаемый пароль выписывался без повторов букв в квадрат; в оставшиеся клетки в алфавитном порядке выписывались буквы алфавита, отсутствующие в пароле. Например, пусть паролем является слово «The table». Тогда квадрат имеет следующий вид:

Такой квадрат уже не нужно иметь при себе. Достаточно запомнить ключ – пароль. Заметим, стати, что таким же образом можно запомнить порядок расположения букв при использовании «линейки Энея», а также шифра обобщенной замены Ю.Цезаря (при произвольном расположении букв в нижней строке). Интересное усиление шифра Полибия было предложено одним криптографом-любителем уже в ХІХ веке. Смысл этого усложнения поясним на примере.

Пусть имеет следующий квадрат Полибия:

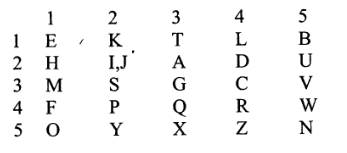
Зашифруем по нему слово «The apple». Получим шифрованный текст ___________________ 13.21.11.23.42.42.14.11.

На этом историческое шифрование по Полибию заканчивалось. Это был шифр простой замены типа шифра Цезаря, в котором каждая буква открытого текста заменялась на некоторое двухзначное десятичное число, и эта замена не менялась по своему тексту. Количество ключей этого шифра равно 25!

Усложненный вариант заключается в следующем. Полученный первичный шифртекст (*) шифруется вторично. При этом он выписывается без разбиения на пары: 132111234242411 (**).

Полученная последовательность цифр сдвигается циклически в лево на один шаг: 3211123424214111.

Это последовательность вновь разбивается в группу по два: 32.11.12.34.24.21.41.11. И по таблице заменяется на окончательный шифртекст: SEKCDHFE. (***).

Количество ключей в этом шифре остается тем же (25!), но он уже значительно более стоек. Заметим, что шифр уже не является шифром простой замены (буква Е открытого текста переходит в различные буквы: К,Е; буква Р – в буквы D,H).

Был подмечен и негативный момент. Если в шифре простой замены шифр текста будет написан с одной ошибкой (например, в тексте (*) вместо четвертой буквы 23 будет написано 32), то расшифрованный текст будет содержать лишь одну ошибку: The spple, что легко исправляется получателем сообщения.

Если же в тексте (***) будет искажена четвертая буква (буква С заменена, например, на К), то в расшифрованном тексте будет уже два искажения: The hiple, что уже затрудняет восстановление исходного сообщения. Анологично обстоит дело с ошибками вида «пропуск букв». Пусть в тексте (***) пропущена буква С. Шифртекст примет вид: SEKDHFE, ИЛИ 32.11.12.24.21.41.11.

После расшифрования получим: The іple, то есть на ряду с пропуском буквы в расшифрованном тексте имеется и искажение другой буквы. При пропуске в (***) первой буквы при расшировании получим: Еe аpple.

· Шифр Чейза.

В середине ХІХ века американец П.Э.Чейз предложил следующую модификацию шифра Полибия.

Выписывается прямоугольник размера 3*10; буквы латинского алфавита дополняются знаком @ и греческими буквами λ, ω, φ:

Ключом шифра является порядок расположения букв в таблице. При шифровании координаты букв выписываются вертикально. Например, слово PHILIP преобретает вид: 1 3 3 1 3 1

9 5 9 8 9 9

Чейз предложил ввести еще один ключ: заранее оговоренное правило преобразования нижнего ряда цифр. Например, число, определяемое этим рядом, умножается на 9:

959899х9=8639091

получаем новую двухстрочную запись: 1 3 3 1 3 1

8 6 3 9 0 9 1

Эта двухстрочная запись вновь переводится в буквы согласно таблице; при этом первое число (8) нижнего ряда определяет букву первой строки. Шифртекст приобретает следующий вид: L N S I φ I X (**).

Могуть быть использованы и другие преобразования координат. Этот шифр значительно сильнее шифра Полибия; он уже не является шифром простой замены.

При рассшифровании полученная последовательность (**) переводится в двухстрочную запись:

(1) 1 3 3 1 3 1

8 6 3 9 0 9 1

Нижний ряд делится на 9: 8 6 3 9 0 9 1: 9=9 5 9 8 9 9, образуется двухстрочная запись (*) и по ней согласно таблице читается открытый текст.

Однако предложение Чейза не нашло поддержки. Причины: заметное усложнение процесса шифрования – рассшифрования, а также особая чувствительность шифра к ошибкам (искажениям в шифртекте). В этом читатель сможет убедиться самостоятельно. Кроме того, использование в качестве ключа любого числа (кроме 9) может порождать недоразумения как при шифровании, так и при расшифровании.

· Магические квадраты

Во времена средневековья европейская криптография приобрела сомнительную славу, отголоски которой слышатся и в наши дни. Криптографию стали отождествлять с черной магией, с некоторой формой оккультизма, астрологией, алхимией, еврейской каббалой. К шифрованию информации призывались мистические силы. Так, например, рекомендовалось использовать «магические квадраты».

В квадрат размером 4 на 4 (размеры могли быть и другими) вписывались числа от 1 до 16. Его магия состояла в том, что сумма чисел по строкам, столбцам и полным диагоналям равнялась одному и тому же числу – 34.

В первые эти квадраты появились в Китае, где им и была приписана некоторая «магическая сила». Приведем пример:

Шифрование по магическому квадрату производилось следующим образом. Например, требуется зашифровать фразу: «Приезжаю сегодня». Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам, а в пустые клетки ставятся произвольные буквы.

16 У	3 И	2 Р	13 Д
5 З	10 Е	11 Г	8 Ю
9 С	6 Ж	7 А	12 О
4 Е	15 Я	14 Н	1 П

После этого шифрованный текст записывается в строку: УИРДЗЕГЮСЖАОЕЯНП.

При расшифровании текст вписывается в квадрат и открытый текст читается в последовательности чисел «магического квадрата». Данный шифр – обычный шифр перестановки, но считалось, что особую стойкость ему придает волшебство «магического квадрата».

· Шифр Аве Мария

В XVвеке аббат Тритемий (Германия) сделал два новаторских предложения в области криптографии: он предложил шифр «Аве Мария» и шифр, построенный на основе периодически сдвижемого ключа.

Шифр «Аве Мария» основан на принципе замены букв шифруемого текста на заранее оговоренные слова. Из этих сообщений составлялось сообщение. Приведем пример.

Заменим буквы Е, Н, Т на следующие слова:

Е = «Зеленый», «Жду», «Мой»: Н = «И», «Я», «Здесь»;

Т = «Дома», «Вечером», «Около», «Ключ».

Тогда отрицательный секретный ответ «нет» на заданный вопрос может иметь несколько вариантов: «Я жду дома», «Я жду вечером», «Здесь мой ключ».

· Шифры Вольных Каменщиков

Вспомним шифр «Братства Франкмасонов», или «Вольных каменщиуков», который они использовали для общения между собой. По современным понятиям и вопреки расхожему мнению он совершенно не стоек, но преставляет определенный интерес. Приведем небольшой пример (применительно к английскому языку). Нарисуем три фигуры следующего вида:

В соответствии с этими фигурами буквы получают следующее геометрическое представление:

Интересно, что при походе на Россию Напалеон использовал в низших звеньях своей связи подобные шифры. Они были раскрыты русскими специалистами, что оказало определенное влияние на ход боевых действий.

· Шифры Ардженти

В XVI веке заметный вклад в развитие криптографии внес криптограф папы римского Маттео Ардженти, унаследовавший искусство тайнописи от своего дяди. Именно Ардженти предложил использовать слово-пароль для придания алфавиту легко запоминаемого смешанного вида. Об этом уже говорилось при рассмотрении усложненного шифра Полибия.

Ардженти рекомендовал не разделять слова, применять омофонные замены, вставлять в шифртекст большое количество «пустышек», устронять пунктуацию, не вставлять в шифртекст открытые слова («клер») и т.д. Для затруднения дешифрования шифров замены он предложил следующее: заменять буквы, либо на цивры (от 0 до 9), либо на числа (от 00 до 99), приче во избежание путаницы при расшифровании цифры, непользуемые как самостоятельные цифробозначения, не должны входить в двухзначные обозначения.

Поскольку однозначных обозначений оказывается сравнительно немного, то чтобы не бросалось в глаза их малая частота появления в шифвртексте, Ардженти рекомендовал придавать однозначные обозначения наиболее часто встречающимся в открытом тексте буквам.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: