Показатели эффективности и неэффективности чистых стратегий игроков.

Решение игры в смешанных стратегиях.

 

Если нижняя V и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение V — V = называется ценой игры в смешанных стратегиях. Нижняя и верхняя цены игры в чистых стра­тегиях и и цена игры в смешанных стратегиях V связаны между собой неравенствами < V< .

Стратегии P° и Q° соответственно игроков А и В, удовлетворяющие равенствам V — а(Р°) = (Q°) (и тогда это общее значение очевидно равно Н(Р°, Q°)), называются оптимальными смешанными стратегия­ми соответственно игроков A и В.

Таким образом, оптимальные смешанные (в частности, чистые) стратегии Р° и Q⁰ соответственно игроков А и В обладают тем свой­ством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптималь­ной стратегии.

Множества оптимальных смешанных стратегий соответственно игроков А и В обозначим через (S_A)° и (S_B)°.

Полным решением игры в смешанных стратегиях называется трех­элементная совокупность {(S_A)°,(S_B)°, V}. Любая пара оптималь­ных стратегий Р° и Q⁰ соответственно игроков А и В и цена игры в смешанных стратегиях V образуют частное решение в смешанных стратегиях.

 

Теорема 1. (Основная теорема матричных игр Дж. фон Неймана.) Любая матричная игра имеет решение в смешанных страте­гиях, т.е. существуют цена игры в смешанных стратегиях V и оптималь­ные смешанные стратегии Р° и Q⁰ соответственно игроков А и В, т.е.

 

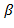V = V = max (Р)= = min (Q) = (Р°) = (Q°) = Н(Р°, Q°).

 

Теорема 2. (Свойство равнозначности седловых точек.) Если (х ', у') и (х", у") — седловые точки функции f (x, у) на декартовом произведении Х x Y, то значения данной функции в этих точках совпада­ют: f (x', у') = f (x",y").

 

Теорема 3. (Свойство взаимозаменяемости седловых то­чек.) Если (х', у') и (х", у") — седловые точки функции f(x, у) на декар­товом произведении Х x Y, то (х', у") и (х", у') — также седловые точки функции / (х, у) на множестве X x Y.

 

Теорема 4. (Критерий существования седловой точки.) Для того чтобы функция f (х, у), х X, у Y, имела седловую точку на де­картовом произведении X x Y, необходимо и достаточно, чтобы суще­ствовали

 

max inf f(x,у) и min sup f(x,у)

и выполнялось их равенство

max inf f(x,у) = min sup f(x,у)

 

Теорема 5. Если множества X R^m и Y Rⁿ — выпуклые компакты, а функция f(x, у) непрерывна по совокупности переменных (х, у) X x Y u вогнуто-выпукла (выпукло-вогнута) на X xУ, то у нее на декартовом произведении X x Y существуют седловые точки.

Определение и существование показателя эффективности смешанной стратегии игрока А относительно множеств смешанных и чистых стратегий игрока В.

Теорема 1. Для каждой смешанной (в частности, чистой) стратегии Р е S_A игрока А существует (достигается)

 

a(P;S_B) = min H(P,Q).

 

Для каждой смешанной (в частности, чистой) стратегии Q S_B игрока В существует (достигается)

 

(Q;S_A) = max H(P,Q).

 

Число а(Р; S_B) называется показателем эффективности смешан­ной стратегии Р S_A игрока А относительно множества S_B смешанных стратегий игрока В.

 

Число а(Р; ) = min Н(Р, Q) = minH(P, Вj)

 

называется показателем эффективности смешанной стратегии Р S_A игрока А относительно множества чистых стратегий игрока В. В частности, если Р = Аi — чистая стратегия, то а( ; ) = — показатель эффективности чистой стратегии (относительно множества чистых стратегий игрока В).

 

Теорема 2 (НЕ НУЖНО). Показатели эффективности любой смешанной (в частности, чистой) стратегии Р S_A игрока А относительно множесте и S_B соответственно чистых и смешанных стратегий про­тивника В равны:

а(Р; )= а(Р; )

 

Показатели эффективности и неэффективности чистых стратегий игроков.

Рассмотрим матричную [ m х n ] - игру с игроками А и В, задаваемую матрицей выигрышей A.

Показателем эффективности стратегии A i назовем минимальный выигрыш при этой стратегии (т.е. минимальный элемент i -й строки матрицы A):

 

 

Максимином, или нижней ценой игры в чистых стратегиях, на­зывается наибольший из показателей эффективности стратегий Аi, i = 1, 2,..., т,

 

 

Стратегия A_k, показатель эффективности которой совпадает с мак­симином а_к = а, называется максиминной стратегией игрока А. Мно­жество всех (чистых) максиминных стратегий игрока А обозначим через . Принцип выбора игроком А максиминной стратегии в качестве эффективной называется максиминным принципом. Если игрок А придерживается максиминного принципа выбора стратегий, то ему при любой игре противника В гарантирован выигрыш в чистых стратегиях, не меньший максимина а.

Показателем неэффективности стратегии Bj назовем максималь­ный проигрыш игрока В при этой стратегии (т.е. максимальный эле­мент j -го столбца матрицы А):

Минимаксом, или верхней ценой игры в чистых стратегиях, назы­вается наименьший из показателей неэффективности стратегий B_j, j = 1,2,..., п:

 

Стратегия , показатель неэффективности которой совпадает с ми­нимаксом , называется минимаксной стратегией игрока В. Мно­жество всех (чистых) минимаксных стратегий игрока В обозначим через . Принцип выбора игроком В минимакснои стратегии в качестве эффективной называется минимаксным принципом. Если игрок В придерживается минимаксного принципа выбора стратегий, то он при любой игре противника А не может проиграть больше мини- макса .

Поделиться:

Воспользуйтесь поиском по сайту: