Угол между прямой и плоскостью.

Расстояние от точки до плоскости.

Найдём расстояние от точки М₀ до плоскости a:Ax+By+Cz+D=0 (рис.1). d=|М₁М₀|, т.к. N||М₁М₀ÞNМ₁М₀=±|N||М₁М₀|=±|N|d; A(x-x₀)+B(y-y₀)+C(z-z₀)=±|N|d; Ax₀+By₀+Cz₀+D–(Ax₁+By₁+Cz₁+D)=±|N|d; Ax₀+By₀+Cz₀+D=±|N|dÞd=|Ax₀+By₀+Cz₀+D|/(ÖA²+B²+C²).

Параметрические и канонические уравнения прямой линии в пространстве.

= =(x_B-x_A; y_B-y_A; z_B-z_A). Поскольку векторное равенство эквивалентно трем координатным, получаем, что М? l тогда и только тогда, когда x=x_A+ta_x, y=y_A+ta_y, z=z_A+ta_z (a_x= x_B-x_A, a_y=y_B-y_A, a_z=z_B-z_A (**)). (*), если знаменатель одной из дробей равен нулю, то равен нулю и числитель этой дроби. Например, если a_y=0, а a_z≠0, то систему уравнений надо понимать так: y=y_A, a_x=(z-z_A)=a_z(x-x_A). Если a_y=y_B-y_A=0 и a_z=z_B-z_A=0, то система уравнений (*) принимает вид y=y_A, z=z_A, т.е. определяет прямую l= (АВ), параллельную оси абсцисс и проходящую через точку A (x_A; y_A; z_A). Параметрические уравнения (**) этой прямой имеют вид x=x_A+ta_x, y=y_A, z=z_A где (a_x≠0). Так как a_x=x_B-x_A, a_y=y_B-y_A, a_z=z_B-z_A, то система уравнений, определяющих прямую l=(АВ), которая проходит через 2 заданные точки A (x_A; y_A; z_A) и B (x_B; y_B; z_B), может быть записана также в виде . Это уравнение называется каноническим уравнением прямой l в пространстве.

 

– канонические уравнения прямой.

– параметрическое уравнение прямой.

 

Прямая как пересечение двух плоскостей. Переход к параметрическим (каноническим) уравнениям прямой.

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

 

– канонические уравнения прямой.

– параметрическое уравнение прямой.

 

Угол между двумя прямыми в пространстве.

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим:

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

 

Расстояние от точки до прямой (в пространстве).

Пусть дана прямая :

и – точка, не принадлежащая этой прямой. Обозначим – направляющий вектор прямой , – точка на прямой , – расстояние от точки до .

Рассмотрим параллелограмм, построенный на векторах и . Тогда – высота этого параллелограмма, опущенная из вершины . Следовательно,

.

Расстояние между двумя прямыми в пространстве.

Пусть даны две скрещивающиеся прямые

: и : ,

и – расстояние между и .

Построим плоскость , проходящую через прямую параллельно . Тогда – расстояние от прямой до плоскости . Найти это расстояние можно по формуле:

,

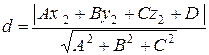где 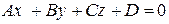– общее уравнение плоскости ,

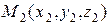– любая точка на прямой .

Угол между прямой и плоскостью.

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

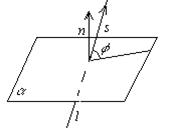Рассмотрим векторы 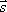и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда .

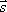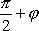Если угол между векторами и тупой, то он равен . Следовательно 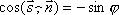. Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой 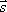и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы 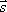и перпендикулярны.

Поделиться:

Воспользуйтесь поиском по сайту: