Третья система соразмерности «Золотое сечение» («Золотое отношение»)

Пропорции и пропорционирование.

Соразмерность частей и целого в архитектурной композиции.

Соразмерность и ее математическое выражение.

Единство произведения зодчества должно выражаться в закономерной взаимосвязи размеров его частей и целого.

Соразмерность частей здания определяется его назначением и тектонической структурой, она получает зримое выражение в системе пропорций. Эта система должна быть создана в рамках, обусловленных целесообразным функциональным и конструктивным решением.

Средством художественного воздействия система пропорций может стать при условии, что она будет восприниматься зрителем.

В математике пропорцией называется равенство двух отношений – a: b = c: d

Члены пропорции взаимосвязаны, любой из них может быть определен по трем остальным. Сравнение двух величин мы называем отношением. Для образования пропорции необходимы два или несколько взаимосвязанных отношений.

 

Композиционной значимостью обладают именно пропорции, в которых раскрываются внутренние закономерности связи форм. Отдельно взятое отношение не может быть ни прекрасным, ни безобразным- эстетическую значимость оно получает лишь войдя в закономерную связь с другими, образуя пропорцию.

 

Для архитектора отношения и пропорции важны не в числовом выражении, а в применении к соотношениям конкретных элементов сооружения.

Пользуясь математическими закономерностями, архитектор приводит к гармонии формы, имеющие определенную сложную конструктивную структуру и жизненное назначение.

Согласование геометрических параметров частей сооружения необходимо, без него не возникает произведение зодчества, но не его математическое выражение изначально в образовании форм.

В математическую пропорцию должна быть облечена закономерность, к которой вчерне уже приведена сложная система композиции.

В эскизах архитектор должен нащупать такую закономерность. А способы пропорционирования должны помочь ему найти окончательную форму для выражения художественно осознанного единства.

Пропорциональная взаимосвязь элементов может быть выражена в соотношениях линейных отрезков и в геометрическом подобии фигур.

Соотношение отрезков воспринимается легко, если их чередование развивается по одной вертикали, как, например, соотношение высоты неравных этажей.

Сравнение вертикальных отрезков, расположенных в различных плоскостях, зрительно же воспринимается, так как искажается перспективными ракурсами.

Так же не имеет смысла сравнение вертикальных и горизонтальных отрезков.

Но здесь мы переходим к другой категории-соразмерности геометрических фигур.

Диагонали подобных прямоугольников параллельны при параллельном размещении идентичных сторон, и перпендикулярны при развороте прямоугольников на 90 º

Такое расположение диагоналей – признак подобия фигур, а следовательно и простейшей пропорциональной зависимости.

Прием объединения композиции приведением прямоугольных форм к подобию часто используется в архитектуре.

Подобие прямоугольников легко воспринимается при фронтальном наблюдении объектов. Ракурс - даже незначительные – уничтожают аналогию между прямоугольниками, вытянутыми по горизонтали и вертикали.

Но для фигур с параллельными диагоналями она сохраняет свое значение и при сокращениях довольно резких – эту особенность необходимо учитывать.

Геометрическое подобие фигур, которое не может быть воспринято в натуре, не имеет никакой композиционной ценности. (Так не имеет смысла приводить к нему очертания на плане)

 

Повторение геометрически подобных форм- лишь частный случай соразмерности композиции. Вычлененная из целого часть, подобная его общему очертанию, сама по себе хорошо связывается с ним.

Но расчленение образует и другие формы. Сразу возникает задача связать и эти элементы общей пропорциональной закономерностью, определить их место в системе целого и их соотношение с другими элементами.

 

Пропорция, связывающая между собой две формы - a: b = c: d, - должна войти в систему, охватывающую все части архитектурного организма.

Простое продолжение пропорционального ряда не может создать необходимый эквивалент, поэтому возникают новые производные виды пропорциональной зависимости.

Эти ряды зависимостей должны сложиться в единый пропорциональный строй композиции.

Пропорциональный строй должен отвечать обязательному требованию гармонии – сочетать единство и многообразие.

Цельность – необходимое условие самого существования композиций, многообразие необходимо для ее содержательности.

Последовательный ряд подобных фигур может быть связан двумя основными видами закономерности возрастания, основанными на арифметической или геометрической прогрессии.

В первом случае каждая в ряду фигур больше предыдущей на одну и туже величину:

A-B =B-C=C-D....и т.д.

(1, 2, 3, 4, и т.д. (+1))

(Такой ряд в архитектуре связывается с выражением соотношения частей в простых целых числах)

Во втором случае каждая последующая фигура возрастает по сравнению с предыдущей в одно и то же число раз:

 

A: B =B: C=C: D....и т.д.

( 1* 2=2, 4, 8, 16)

Возникающая таким образом геометрическая пропорция называется непрерывной.

Третья система соразмерности «Золотое сечение» («Золотое отношение»)

A: B = B: (A+B)

Особенность «золотого сечения» заключается в том, что эта пропорция связывает между собою отношения частей и целого.

Непрерывный ряд «золотого сечения» выражает идею деления целого на свои подобия таким образом что, возникшие величины, складываясь, могут воссоздать исходный размер.

Ряд «золотого сечения» может стать основой соразмерности бесконечного множества величин, с другой стороны – взаимопроникающая соразмерность возникает в этом ряду уже между двумя величинами – (меньшая относится к большей так же, как большая относится к их сумме)

В количественном выражении ряд «золотого сечения» может быть представлен следующим образом:

...0,056; 0,090; 0,146; 0,236; 0,382;

0,618; 1.0; 1, 618; 2, 618;... и т.д.

Значения – эти приближенные.

Отношение любых двух соседних чисел ряда можно выразить числом 0, 618, а в точном значении –

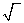5-1, и весь ряд состоит из чисел иррациональных.

 

Подобным свойствам обладает и ряд целых чисел, открытый в XIII веке итальянским математиком Леонардо из Пизы, прозванным Фибоначчи –

- 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... и т.д.

Отношение двух соседних чисел в этом ряду по мере возрастания их количественной величины сближается с отношением «золотого сечения» - 0, 618.

 

(3: 5=0,6; 5: 8 = 0, 625; 8: 13 = 0, 615 и т.д.)

 

1. Деление отрезка в «золотом отношении» легко осуществляется с помощью геометрических построений.

Так в прямоугольном треугольнике катеты которого относятся, как 1: 2, большой катет членится в «золотом отношении» разностью между малым катетом и гипотенузой.

2. Полуокружность, описанная вокруг квадрата, позволяет построить два примыкающих к нему прямоугольника с «золотым отношением» сторон.

Длинная сторона прямоугольника, образованного этими тремя фигурами, будет равна 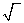5, если сторону квадрата мы примем за 1.

 

При этом большой прямоугольник, с отношением сторон 1: 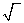5, может рассматриваться как сумма двух прямоугольников «золотого отношения» - малого, расположенного вертикально, и второго, горизонтального, образованного из квадрата.

Обратим на это внимание в геометрических зависимостях. Здесь обнаруживается связь между «золотым отношением» и другими иррациональными отношениями, находящими применение в архитектуре.

К числу их принадлежит 1: 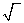5 - отношение диагонали прямоугольника (составленного из 2-х квадратов), к его короткой стороне.

Интересный ряд образуется на основе отношения 1: 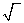2, характеризующего связь между стороной квадрата и его диагональю. В этом ряду примечательно чередование иррациональных и простых чисел:

1,0: 1, 414: 2,0: 2, 828: 4: 5, 656: 8, 0: 11, 312: 16, 0 и т.д.

 

На основе соотношений стороны и диагонали квадрата и прямоугольника, образованного из двух квадратов, могут быть развиты связанные, взаимопроникающие ряды, составленные из простых и иррациональных чисел.

Построение показывает, как, откладывая на продолжении основания диагональ вертикального прямоугольника ABCD, составленного из двух квадратов, мы получаем прямоугольник ABEF, соотношение сторон которого = 2 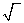5.

Одновременно возникает и прямоугольник CDEF с соотношением сторон 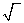5-1 (прямоугольник «золотого сечения») 2

Диагональ АЕ, отложенная на продолжении стороны AF, определит нам сторону нового прямоугольника ABHG. Соотношение его сторон – 2:3.

Часть его - CDGH- квадрат.

Таким образом, повторяя один и тот же прием построения, мы пришли сначала от целочисленных отношений к иррациональным и вновь вернулись к целочисленным.

Следующий цикл операций вновь приводит нас к иррациональным отношениям, причем добавленный нами прямоугольник GHIK будет состоять из двух прямоугольников «золотого сечения».

Квадрат является исходной фигурой нашего построения, он возникает и в последовательности геометрических операций.

Очевидно, что связанное с ним соотношение 1: 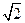неразрывно с той системой взаимосвязей, которую раскрывает анализ.

Исследования ученых привели к убеждению, что именно в построении взаимопроникающих подобий заключены забытые секреты пропорционального строя произведений архитектурной классики.

Слаженные гармоничные системы, в которых переплетаются соотношения простых и иррациональных чисел, создавались с помощью нетрудных геометрических построений.

Исходными фигурами для них служили квадрат и прямоугольник, составленный из двух квадратов, а в некоторых случаях так называемый «священный египетский треугольник»

(Прямоугольный треугольник, соотношение длин катетов и гипотенузы которого составляет 3: 4: 5, единственный треугольник, величины сторон которого образуют арифметический ряд.)

Системы эти опирались на технические приемы возведения зданий, способы определения в натуре размеров их частей.

Пропорционирование, как метод количественного согласования частей и целого имеет в своей основе геометрическую или числовую закономерность, которая способствует достижению эстетической целостности, гармоничности объемно-пространственной формы за счет объединения ее размеров в какую-либо систему.

Особенности пропорциональных систем связаны со способами строительства и измерения, которые применялись архитекторами разных эпох.

В древности пропорциональные системы получали с помощью мерного шнура и копьев путем геометрических построений на основе треугольника, квадрата, прямоугольника или круга.

Система пропорционирования на основе вписанных квадратов давала геометрический ряд с отношением 1: 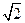, в котором чередовались иррациональные и целые простые числа.

Эта система использовалась как в Египте, так и в более поздние времена, например в средневековье для построения готических башен;

Так же отношение стороны и диагонали квадрата связывают древнерусскую сажень и косую сажень.

Система вписанных равносторонних треугольников дает ряд на основе двух чередующихся отношений: стороны треугольника к высоте (2/ 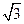) и высоты к половине стороны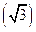

Пропорционирование на основе равностороннего треугольника применялось в средневековье, где система триангулирования пронизовала всю структуру готических соборов, однако отношения, свойственные этой системе, могут быть обнаружены и в архитектуре других эпох, например в архитектуре Древней Греции.

В золотом отношении находятся стороны равнобедренных треугольников с углами 36°, 72° и 72° или 108°, 36° и 36°. Поскольку диагонали правильного пятиугольника рассекают его на треугольники именно с такими углами, ряд золотого сечения может быть получен также на основе пентаграммы – пятиугольной звезды, образованной продлением сторон правильного пятиугольника или звездчатого десятиугольника.

 

Геометрическая прогрессия.

Основным свойством арифметического гармонического и геометрического рядов, является то, каждое из чисел представляет собой соответственно среднее арифметическое, среднее гармоническое и среднее геометрическое предыдущего и последующего членов.

Так в арифметической прогрессии 1, 2, 3

число 2 = (3+ 1)/ 2

В гармонической прогрессии , , ,

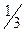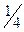число 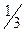= 2 / 2 + 4,

В геометрической прогрессии 1, 2, 4, число 2 =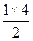

Поэтому числа арифметического, гармонического и геометрического рядов называют средними числами.

Средние числа издавна служили архитекторам, скульпторам и художникам в качестве средства достижения гармоничных соотношений.

 

«Золотое сечение»

Золотое сечение выражают обычным числом 1, 618 или обратным ему числом 0, 618, для которых приняты символы Ф или 1/Ф.

Эти числа являются знаменателями возрастающего (Ф) и убывающего (1/Ф) рядов золотого сечения.

Особенностью этих чисел является их способность при сложении с единицей (для Ф) и при вычитании из единицы (для 1/Ф) давать квадраты самих себя, т.е. 1 + Ф = Ф²;

1 – 1/Ф = (1/Ф)²

«Золотое сечение» - это единственная геометрическая прогрессия, обладающая признаком аддитивного ряда ()

Пропорция в архитектуре – любая закономерность в соотношениях величин, которая связывает отдельные части и параметры формы в единое целое.

Таким образом, пропорция в архитектуре есть понятие, отражающее однородность (закономерность) изменений количественной меры при переходах от одной части формы к другой и к форме в целом.

 

Виды пропорциональных отношений.

Арифметическая прогрессия, выражается рядом чисел, в котором каждое последующее число больше предыдущего на одну и ту же величину:

0, 1, 2, 3, 4, 5, 6..........т.д. (мерная линейка)

По мере возрастания ряда – отношения (математические) между соседними числами развиваются от контрастных к нюансным, приближаясь в пределе к равенству.

( и )

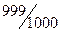Гармоническая прогрессия – это ряд чисел обратных ряду чисел арифметической прогрессии:

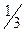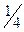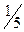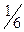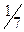, , , , , . Она лежит в основе музыкального строя.

Отношения (математические) между соседними членами гармонического ряда по мере его возрастания так же, как и в арифметической прогрессии, изменяются от контрастных к нюансным.

 

Геометрическая прогрессия представляет собой ряд чисел, в котором каждое последующее число больше (или меньше) предыдущего в одно и то же число раз.

(1, 2, 4, 8, 16....; 1, , , )

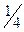Отношение между соседними членами геометрического ряда на всем его протяжении остается постоянным, равным знаменателю прогрессии.

Перечисленные системы пропорционирования являются геометрическими, в числовом выражении они менее удобны в использовании, так как включают иррациональные числа.

Но существуют пропорциональные системы, основанные на числовых (арифметических) приемах согласования частей и целого; это так называемые модульные системы.

Простейшим применением модульной системы является масштабная сетка, в которую вписываются как общий абрис, так и детали сооружения.

Модульная система пропорционирования предполагает существования модуля – условной единицы измерения.

Модульные пропорции широко применялись на протяжении всего развития архитектуры.

Наиболее ярким примером модульной системы пропорционирования является построение античных орденов, в которых в качестве модуля используется либо диаметр, либо радиус колонны.

Применяемая в нашей стране модульная система (ЕМС) так же использует единый (М = 100 см.), на основе которого путем его членения или умножения получают все принятые в строительстве размеры.

 

Пропорционирование может быть использовано в двух основных направлениях: как метод создания целостной формы и как метод выявления закономерностей построения уже созданных архитектурных форм.

При этом следует понимать, что закономерности, выявленные в уже созданных архитектурных формах, далеко не всегда осознано применялись их создателями.

Следует помнить, что пропорционирование – достаточно сильное, но далеко не единственное средство гармонизации архитектурной формы и поэтому одно только совершенство пропорции еще не является гарантом получения совершенного архитектурного произведения.

Поделиться:

Воспользуйтесь поиском по сайту: