 |
Расчет однородной линии с распределенными параметрами в установившемся режиме
|
|
|
|
Верхний провод назовем прямым. Нижний провод - обратным.
Пусть известны первичные параметры однородной линии, отнесенные к единице длины:
r0 - сопротивление прямого и обратного проводов [Ом/м];
L0 - индуктивность петли, образуемой прямым и обратным проводами [Гн/м];
g0 - проводимость (утечка) между проводами [См/м]; g0≠1/r0;
С0 - ёмкость между проводами [Ф/м];
x - расстояние от начала линии до текущего элемента её длины;
u, i - напряжение и ток в начале выбранного элемента линии dx.
и - напряжение и ток в начале следующего элемента линии.
На основании законов Кирхгофа:
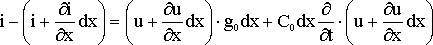
Приведем подобные члены, пренебрегая величинами второго порядка и сокращая на dx получаем дифференцированное уравнение:
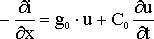
Если токи и напряжения синусоидальные, то можно воспользоваться комплексным методом.
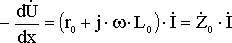
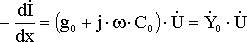
- комплексное сопротивление линии единичной длины.
- комплексная проводимость линии единичной длины.
Продифференцируем по x уравнения:
Заменим dİ/dx и dÚ/dx из предыдущих уравнений:
Решение имеет вид:
(6.1)
- коэффициент распространения.
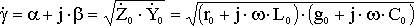(6.2)
α - коэффициент затухания;
β - коэффициент сдвига фаз;
- комплексные постоянные интегрирования [В].
Найдем ток:
(6.3)
- волновое (характеристическое) сопротивление линии (от длины не зависит).
(6.4)
(6.5)
Волновое сопротивление и коэффициент распространения называют вторичными параметрами однородной линии.
Чтобы найти нужно задаться входными напряжениями 
и током İ1 и принять x=0 (начало линии).
Решаем систему уравнений:
(6.6)
(6.7)
Подставляем в основное решение и получим уравнения линии с гиперболическими функциями:
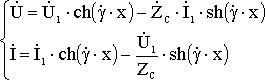(6.8)
Если известны комплексные значения 
и İ2 в конце линии, то 
и İ в любой точке линии на расстоянии x от её конца можно записать так:
|
|
|
(6.9)
Отсюда получим уравнения, связывающие Ú1 и İ1 с Ú2 и İ2:
(6.10)
где
l - длина линии.
Уравнения аналогичны основным уравнениям четырехполюсника.
6.2 Волны в линии
Выразим комплексы в показательной форме:
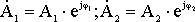(6.11)
Запишем мгновенные значения напряжения и тока:
(6.12)
Умножение на 
выполнено для перехода от действующих значений к амплитудам. Каждое из слагаемых в правой части можно рассматривать как бегущую волну, движущуюся в направлении возрастания или убывания координаты x и затухающую в направлении движения.
Фазовой скоростью волны с называется скорость перемещения фазы колебания, которая в течении времени t и по мере увеличения расстояния x, пройденного волной, остается постоянной, т.е.:
, (для первого слагаемого).
Продифференцируем по времени:
(6.13)
Аналогичное исследование второго слагаемого правой части равенства дало бы для фазовой скорости то же значение, но с обратным знаком. Отсюда заключаем, что эти слагаемые могут рассматриваться как волны, движущиеся в противоположных направлениях. Волны, движущиеся от источника, называют прямыми (падающими), а к источнику - обратными (отражёнными).
Длиной волны λ называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания, в которых различаются на 2π.
Таким образом, найдем длину волны:
(6.14)
Рисунок 6.2 - Волны напряжения в линии
Длина линии может быть задана электрической длиной измеряемой в λ:
(6.15)
Отсюда следует, что токи и напряжения как прямой, так и обратной волны связаны между собой законом Ома.
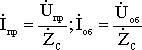
Величины являются комплексными амплитудами для падающей и отражённой волн и зависят от величины входного напряжения, параметров линии и от сопротивления нагрузки на конце линии.
6.3 Длинная линия как четырехполюсник
|
|
|
Из уравнений длинной линии с гиперболическими функциями, связывающих U1, I1 с U2, I2, можно выделить коэффициенты четырехполюсника ABCD:
(6.16)
Линейный симметричный обратимый четырехполюсник:
Если выходные зажимы разомкнуты (I2=0) (холостой ход), тогда входное сопротивление линии будет:
(6.17)
При этом выходное напряжение линии будет:
[на холостом ходу] (6.18)
Рисунок 6.3 - Зависимость входного сопротивления длинной линии от ее длины в режиме холостого хода
Электрически короткая линия (lэ<λ/4) ведет себя подобно ёмкости. При длине lэ≈λ/4, как последовательный колебательный контур. При длине 
как индуктивность. При длине lэ≈λ/2, как параллельный колебательный контур и т.д.
Бесконечно длинная линия имеет входное сопротивление, равное своему волновому сопротивлению.
Если выходные зажимы замкнуты (Ú2=0) (короткое замыкание):
(6.19)
Рисунок 6.4 - Зависимость входного сопротивления длинной линии от ее длины в режиме короткого замыкания
Зависимость входного сопротивления от длины линии носит противоположный характер (L↔C и параллельный ↔ последовательный).
Измерив входное сопротивление линии в режиме холостого хода и короткого замыкания, можно найти ŻC и γ и r0, g0, C0, L0.
(6.20)
(6.21)
Если на выходе стоит ŻH=ŻC, т.е.: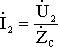 
(6.22)
Если в конце линии стоит сопротивление, равное волновому сопротивлению линии, то такая нагрузка называется согласованной. Входное сопротивление такой линии будет равно волновому независимо от длины этой линии.
При этом:
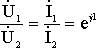(6.23)
Модуль еγl показывает во сколько раз выходные величины уменьшились по сравнению с входными, а аргумент еγl - на сколько сдвинулись по фазе.
Если на выходе стоит ŻH≠ŻС, т.е. (Ú2= İ2 ∙Żн) (общий случай):
(6.24)
При произвольном нагрузочном сопротивлении входное сопротивление представляет собой результат режимов холостого хода и короткого замыкания.
6.4 Изображение падающей и отраженной волн
Найдем комплексные амплитуды напряжения Á1 и Á2:
(6.25)
Для изображения волн примем время t=const.
(6.26)
Если входное воздействие задано функцией синуса, то зависимость напряжения от координаты будет определяться выражением:
(6.27)
Если ŻH=∞(холостой ход):
|
|
|
Если анимация не работает, можно воспользоваться этой прямой ссылкой
(6.28)
В конце разомкнутой линии напряжения падающей и отраженной волн равны. Отражённая волна является зеркальным продолжением падающей.
Если ŻH=0 (короткое замыкание):
Если анимация не работает, можно воспользоваться этой прямой ссылкой
(6.29)
В конце закороченной линии напряжения падающей и отраженной волн равны по модулю и противоположны по знаку (в сумме дают нуль). Отражённая волна является инвертированным зеркальным продолжением падающей.
Если ŻH=ŻC (согласованная нагрузка):
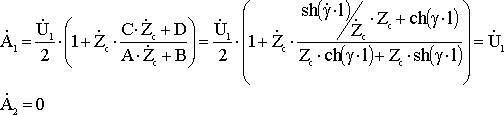
(Отражённая волна не возникает) (6.30)
Отсутствие отражённой волны имеет то преимущество, что вся мощность, переносимая прямой волной к концу линии, поглощается сопротивлением нагрузки.
При наличии обратной волны часть мощности прямой волны возвращается к источнику обратной волной.
Если ŻH≠ŻC (несогласованная нагрузка), возникает отражённая волна, являющаяся результатом наложения отражённых волн при холостом ходе и коротком замыкании.
6.5 Линии без искажений
Неискаженной передачей сигнала называют такую передачу, при которой форма сигнала в начале и конце линии одинакова, но имеет место ослабление и запаздывание сигнала. Она возможна, когда коэффициент затухания, а также фазовая скорость c на всех частотах одинакова. Запишем уравнение для волнового сопротивления:
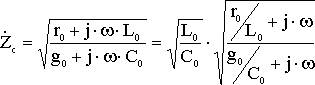(6.31)
Если принять r0/L0=g0/C0 или L0/C0=r0/g0, то от частоты не зависит и является действительной величиной:
(6.32)
Запишем коэффициент распространения, принимая во внимание, что:
и, получим:
- от частоты коэффициент затухания не зависит.
- линейно зависит от частоты, а фазовая скорость
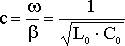от частоты не зависит (6.33)
Таким образом, если для длинной линии соблюдается соотношение L0/C0=r0/g0, то по ней возможна неискажённая передача сигнала.
6.6 Линии без потерь
Для высокочастотных коротких линий, применяемых в радиотехнике, часто можно пренебречь сопротивлением r0 и утечкой g0 по сравнению с ω·L0 и ω·C0. Если принять r0=0 и g0=0, то такую линию называют линией без потерь.
|
|
|
Для линии без потерь:
- волновое сопротивление действительная величина, от частоты не зависит.
- отсутствует ослабление волн.
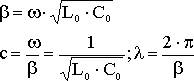(6.34)
Так как аргумент волнового сопротивления равен нулю, то напряжение падающей и отражённой волн совпадают по фазе с токами.
При этом уравнения длинной линии в гиперболических функциях преобразуются в уравнение в тригонометрических функциях:
(6.35)
|
|
|
