| ·
· B1
· B2
· B3
· B4
· B5
· B6
· B7
· B8
· B9
· B10
· B11
· B12
· B13
· B14
· B15
| В статье рассмотрим задачи ЕГЭ по теории вероятности (B6), приведенные к настоящему моменту в открытом банке задач ЕГЭ по математике (mathege.ru), решение которых основано на одной лишь формуле, представляющей собой классическое определение вероятности.
Понять формулу проще всего на примерах. Пример 1. В корзине 9 красных шаров и 3 синих. Шары различаются только цветом. Наугад (не глядя) достаём один из них. Какова вероятность того, что выбранный таким образом шар окажется синего цвета?
Комментарий. В задачах по теории вероятности происходит нечто (в данном случае наше действие по вытаскиванию шара), что может иметь разный результат - исход. Нужно заметить, что на результат можно смотреть по-разному. "Мы вытащили какой-то шар" - тоже результат. "Мы вытащили синий шар" - результат. "Мы вытащили именно вот этот шар из всех возможных шаров" - такой наименее обобщенный взгляд на результат называется элементарным исходом. Именно элементарные исходы имеются в виду в формуле для вычисления вероятности.
Решение. Теперь вычислим вероятность выбора синего шара. Событие А: "выбранный шар оказался синего цвета" Общее число всех возможных исходов: 9+3=12 (количество всех шаров, которые мы могли бы вытащить) Число благоприятных для события А исходов: 3 (количество таких исходов, при которых событие А произошло, - то есть, количество синих шаров) P(A)=3/12=1/4=0,25 Ответ: 0,25
Посчитаем для той же задачи вероятность выбора красного шара. Общее число возможных исходов останется тем же, 12. Число благоприятных исходов: 9. Искомая вероятность: 9/12=3/4=0,75
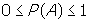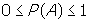Вероятность любого события всегда лежит в пределах от 0 до 1. Иногда в повседневной речи (но не в теории вероятности!) вероятность событий оценивают в процентах. Переход между математической и разговорной оценкой осуществляется путем умножения (или деления) на 100%. Итак,  При этом вероятность равна нулю у событий, которые не могут произойти - невероятны. Например, в нашем примере это была бы вероятность вытащить из корзины зеленый шар. (Число благоприятных исходов равно 0, Р(А)=0/12=0, если считать по формуле) Вероятность 1 имеют события, которые абсолютно точно произойдут, без вариантов. Например, вероятность того, что «выбранный шар окажется или красным или синим» - для нашей задачи. (Число благоприятных исходов: 12, Р(А)=12/12=1)
Мы рассмотрели классический пример, иллюстрирующий определение вероятности. Все подобные задачи ЕГЭ по теории вероятности решаются применением данной формулы. На месте красных и синих шаров могут быть яблоки и груши, мальчики и девочки, выученные и невыученные билеты, билеты, содержащие и не содержащие вопрос по какой-то теме (прототипы285926, 285927), бракованные и качественные сумки или садовые насосы (прототипы 282857, 282856) – принцип остается тем же.
Немного отличаются формулировкой задачи теории вероятности ЕГЭ, где нужно вычислить вероятность выпадения какого-то события на определенный день. (285922, 285923) Как и в предыдущих задачах нужно определить, что является элементарным исходом, после чего применить ту же формулу.
Пример 2. Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20. Какова вероятность того, что доклад профессора М. выпадет на третий день, если порядок докладов определяется жеребьевкой?
Что здесь является элементарным исходом? – Присвоение докладу профессора какого-то одного из всех возможных порядковых номеров для выступления. В жеребьевке участвует 15+15+20=50 человек. Таким образом, доклад профессора М. может получить один из 50 номеров. Значит, и элементарных исходов всего 50. А какие исходы благоприятные? – Те, при которых окажется, что профессор будет выступать в третий день. То есть, последние 20 номеров. По формуле вероятность P(A)= 20/50=2/5=4/10=0,4 Ответ: 0,4
Жеребьевка здесь представляет собой установление случайного соответствия между людьми и упорядоченными местами. В примере 2 установление соответствия рассматривалось с точки зрения того, какое из мест мог бы занять конкретный человек. Можно к той же ситуации подходить с другой стороны: кто из людей с какой вероятностью мог бы попасть на конкретное место (прототипы 282855,282858, 285924, 285928):
Пример 3. В жеребьевке участвуют 5 немцев, 8 французов и 3 эстонца. Какова вероятность того, что первым (/вторым/седьмым/последним – не важно) будет выступать француз.
Количество элементарных исходов – количество всех возможных людей, которые могли бы по жеребьевке попасть на данное место. 5+8+3=16 человек. Благоприятные исходы – французы. 8 человек. Искомая вероятность: 8/16=1/2=0,5 Ответ: 0,5
Немного отличается прототип 285925. Остались задачи про монеты (282854) и игральные кости (285853), несколько более творческие. Решение этих задач можно посмотреть на страницах прототипов.
Приведем несколько примеров на бросание монеты или кубика.
Пример 4. Когда подбрасываем монету, какова вероятность выпадения решки? Исходов 2 – орел или решка. (считается, что монета никогда не падает на ребро) Благоприятный исход – решка, 1. Вероятность 1/2=0,5 Ответ: 0,5.
Пример 5. А если подбрасываем монету два раза? Какова вероятность того, что оба раза выпадет орел? Главное определить, какие элементарные исходы будем рассматривать при подбрасывании двух монет. После подбрасывания двух монет может получиться один из следующих результатов: 1) PP – оба раза выпала решка 2) PO – первый раз решка, второй раз орел 3) OP – первый раз орел, второй раз решка 4) OO – оба раза выпал орел Других вариантов нет. Значит, элементарных исходов 4. Благоприятный из них только первый, 1. Вероятность: 1/4=0,25 Ответ: 0,25
Какова вероятность того, что из двух подбрасываний монеты один раз выпадет решка? Количество элементарных исходов то же, 4. Благоприятные исходы – второй и третий, 2. Вероятность выпадения одной решки: 2/4=0,5
В таких задачах может пригодиться ещё одна формула. Если при одном бросании монеты возможных вариантов результата у нас 2, то для двух бросаний результатов будет 2·2=22=4 (как в примере 5), для трех бросаний 2·2·2=23=8, для четырех: 2·2·2·2=24=16, … для N бросаний возможных результатов будет 2·2·...·2=2N.
Так, можно найти вероятность выпадения 5 решек из 5 бросаний монеты. Общее число элементарных исходов: 25=32. Благоприятных исходов: 1. (РРРРР – все 5 раз решка) Вероятность: 1/32=0,03125
То же верно и для игральной кости. При одном бросании возможных результатов здесь 6. Значит, для двух бросаний: 6·6=36, для трех 6·6·6=216, и т. д.
Пример 6. Бросаем игральную кость. Какова вероятность, что выпадет четное число?
Всего исходов: 6, по числу граней. Благоприятных: 3 исхода. (2, 4, 6) Вероятность: 3/6=0,5
Пример 7. Бросаем две игральные кости. Какова вероятность, что в сумме выпадет 10? (округлить до сотых)
Для одного кубика 6 возможных исходов. Значит, для двух, по вышеупомянутому правилу, 6·6=36. Какие исходы будут благоприятными для того, чтоб в сумме выпало 10? 10 надо разложить на сумму двух чисел от 1 до 6. Это можно сделать двумя способами: 10=6+4 и 10=5+5. Значит, для кубиков возможны варианты: (6 на первом и 4 на втором) (4 на первом и 6 на втором) (5 на первом и 5 на втором) Итого, 3 варианта. Искомая вероятность: 3/36=1/12=0,08 Ответ: 0,08
|
