 |
Пределы числовых последовательностей.
|
|
|
|
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
И ПЛАН ПРОВЕДЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ
Специальность 20.05.01 «Пожарная безопасность»
по учебной дисциплине «Высшая математика»
Тема № 1. Введение в математический анализ.
Занятие 1.4. Вычисление пределов последовательностей.
Учебная группа: 111-114, 103.
Обсуждены на заседании
методической секции «Высшая математика»
Протокол № 12 от
«31» июля 2014 года
I. Цели и задачи занятия
1. Выработать навыки вычисления пределов последовательностей.
2. Показать обучающимся важность данной темы в курсе изучаемой дисциплины.
3. Воспитывать у обучающихся настойчивость в достижении поставленной цели.
II. Расчет учебного времени
| Содержание и порядок проведения занятия | Время, мин |
| ВВОДНАЯ ЧАСТЬ | |
| ОСНОВНАЯ ЧАСТЬ Учебные вопросы: | |
| 1. Пределы числовых последовательностей. | |
| 2. Вычисление пределов последовательностей. | |
| ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Учебно-материальное обеспечение
Классная доска, раздаточный материал.
IV. Методические материалы
К проведению практического занятия
Во вводной части занятия (5 мин.) после объявления темы и целей практического занятия целесообразно изложить последовательность обсуждения учебных вопросов.
Первый учебный вопрос (20 мин).
Пределы числовых последовательностей.
При изложении первого учебного вопроса следует объяснить обучающимся понятие числовой последовательности, их пределов.
Под числовой последовательностью 
понимается функция 
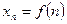, заданная на множестве 
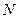натуральных чисел (
– общий член последовательности).
Обозначение: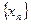 
или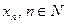 
.
|
|
|
Последовательность 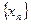называется ограниченной, если существует такое число 
, что для любого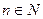 
выполняется неравенство 
. В противном случае последовательность является неограниченной.
Последовательность 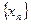называется возрастающей (неубывающей), если для любого 
выполняется неравенство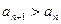 
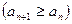. Аналогично определяется убывающая (невозрастающая) последовательность. Любая из представленных выше последовательностей называется монотонной.
Если все элементы последовательности 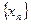равны одному и тому же числу 
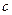, то ее называют постоянной.
Число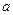 
называется пределом последовательности 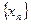, если для любого положительного числа 
найдется такое натуральное число 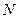, при всех 
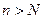выполняется неравенство 
.
Короткое определение предела:
.
Сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся.
Теорема Вейерштрасса (достаточный признак существования предела): Всякая монотонная ограниченная последовательность имеет предел.
На основании теоремы Вейерштрасса: 
(
).
; 
.
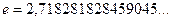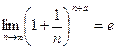Последовательность называется бесконечно большой, если для каждого положительного числа 
найдется такое натуральное число 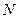, что для 
выполняется неравенство 
. в этом случае считают, что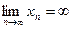 
.
Последовательность называется бесконечно малой, если ее предел равен нулю. Примеры бесконечно малых: 
, 
.
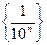Известно, то 
.
Свойства бесконечно малых и бесконечно больших последовательностей:
1. Сумма (разность) б.м. есть б.м. последовательность.
2. Произведение б.м. последовательностей есть б.м. последовательность.
3. Произведение ограниченной последовательности на б.м. есть б.м.
4. Произведение б.м. последовательности на число есть б.м. последовательность.
Теоремы о пределах:
1. 
.
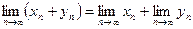2. 
.
2а).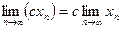 
.
3. 
.
Теорема (теорема о двух милиционерах): Если даны три последовательност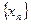и , 
и 
, причем 
(начиная с некоторого номера) для всех и 
, тогда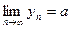 
.
|
|
|
Теорема (предельный переход в неравенствах): Если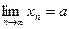 
, 
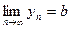и, начиная с некоторого номера, выполняется неравенство 
, то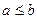 
.
Вопросы для обучающихся:
1.Какие из последовательностей являются ограниченными, монотонными?
а)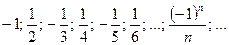 
– ограниченная на отрезке 
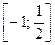, не монотонная.
б)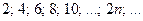 
– неограниченная, монотонно возрастающая.
в)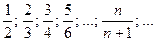 
– ограниченная на отрезке 
, возрастающая.
г) 
– ограниченная, постоянная.
|
|
|
