 |
Матрицы. Виды матриц. Операции над матрицами. Определители квадратных матриц и их свойства. Собственные числа матрицы.
|
|
|
|
1.1
Совокупность чисел, расположенных в виде прямоугольной таблицы, состоящей из  строк и
строк и  столбцов, называют матрицей порядка
столбцов, называют матрицей порядка  (
( на
на  ) и обозначают символом
) и обозначают символом  . В общем виде матрица выглядит так
. В общем виде матрица выглядит так
 .
.
Числа  называют элементами матрицы. Каждый элемент имеет два индекса: первый показывает номер строки, в которой стоит этот элемент, а второй – номер столбца. Размерность матрицы указывать не обязательно. При
называют элементами матрицы. Каждый элемент имеет два индекса: первый показывает номер строки, в которой стоит этот элемент, а второй – номер столбца. Размерность матрицы указывать не обязательно. При  матрицу называют матрицей-строкой, а при
матрицу называют матрицей-строкой, а при  - матрицей-столбцом.
- матрицей-столбцом.
Матрицу, все элементы которой, равны нулю, называют нулевой матрицей и обычно обозначают  . Таким образом,
. Таким образом,  .
.
Если число строк матрицы совпадает с числом ее столбцов, т.е. 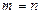 , то матрицу называют квадратной
, то матрицу называют квадратной  порядка и обозначают символом
порядка и обозначают символом  . В квадратной матрице
. В квадратной матрице  элементы с одинаковыми индексами
элементы с одинаковыми индексами  называют элементами главной диагонали, а элементы, сумма индексов которых равна
называют элементами главной диагонали, а элементы, сумма индексов которых равна 
 , элементами побочной диагонали. Во множестве квадратных матриц особую роль играет матрица
, элементами побочной диагонали. Во множестве квадратных матриц особую роль играет матрица
 .
.
Ее называют единичной матрицей. Все элементы ее главной диагонали равны единице, а все остальные элементы – нули.
Квадратную матрицу называют треугольной, если все ее элементы, стоящие ниже или выше элементов главной диагонали, равны нулю. Например, матрицы  и
и  треугольные, причем матрицу
треугольные, причем матрицу  называют верхнетреугольной, а матрицу
называют верхнетреугольной, а матрицу  – нижнетреугольной.
– нижнетреугольной.
Определение 1. Две матрицы одинакового порядка  и
и  называют
называют
равными и пишут  =
=  , если все элементы с одинаковыми
, если все элементы с одинаковыми
индексами обеих матриц совпадают.
Определение 2. Суммой двух матриц  и
и  одинакового порядка
одинакового порядка
называют матрицу  того же порядка, элементы которой
того же порядка, элементы которой
равны суммам соответствующих элементов матриц  и
и  .
.
Определение 3. Произведением матрицы  на число
на число  называют матрицу
называют матрицу
|
|
|
 , все элементы которой равны соответствующим
, все элементы которой равны соответствующим
элементам матрицы  , умноженным на число
, умноженным на число  .
.
Из определения 3 вытекают следующие свойства операции умножения матрицы на число: 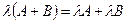 и
и  .
.
Рассмотрим теперь операцию умножения матрицы на матрицу. Пусть имеем матрицу  и матрицу
и матрицу  . Сразу же обратим внимание на размерность матриц: число столбцов матрицы
. Сразу же обратим внимание на размерность матриц: число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . Это условие является необходимым для того, чтобы можно было матрицу
. Это условие является необходимым для того, чтобы можно было матрицу  умножить на матрицу
умножить на матрицу  .
.
Будем рассматривать элементы каждой строки матрицы  как координаты
как координаты  мерных векторов:
мерных векторов:
 ;
;
 ;
;

…………………….
 .
.
Аналогично элементы каждого столбца матрицы  также будем рассматривать как координаты
также будем рассматривать как координаты  мерных векторов:
мерных векторов:
 ;
;
 ;
;
 ;
;
……………………

Произведением матрицы  на матрицу
на матрицу  назовем матрицу
назовем матрицу  .
.
Как видим, элементами матрицы  являются скалярные произведения векторов
являются скалярные произведения векторов  , где
, где  на векторы
на векторы  , где
, где  .
.
Рассмотрим свойства операции умножения матриц. Из определения операции умножения матрицы  на матрицу
на матрицу  вовсе не следует, что можно умножить матрицу
вовсе не следует, что можно умножить матрицу  на матрицу
на матрицу  . Это осуществимо только при условии, что
. Это осуществимо только при условии, что  . В противном случае произведение
. В противном случае произведение  просто не существует. Следовательно, бессмысленно говорить о коммутативности операции умножения матриц. Однако имеют место свойства ассоциативности:
просто не существует. Следовательно, бессмысленно говорить о коммутативности операции умножения матриц. Однако имеют место свойства ассоциативности:  и дистрибутивности:
и дистрибутивности:  ;
;  , которые легко проверяются.
, которые легко проверяются.
Очевидно, что если  и
и  квадратные матрицы одного порядка, то существуют произведения
квадратные матрицы одного порядка, то существуют произведения  и
и  , но нельзя утверждать, что
, но нельзя утверждать, что  . Если же матрицы
. Если же матрицы  и
и  таковы, что
таковы, что  , то их называют перестановочными.
, то их называют перестановочными.
Особую роль при умножении квадратных матриц играет единичная матрица  . Легко показать, что для любой квадратной матрицы
. Легко показать, что для любой квадратной матрицы  имеет место равенство
имеет место равенство  , т.е во множестве квадратных матриц
, т.е во множестве квадратных матриц  порядка матрица
порядка матрица  является аналогом числа 1 во множестве действительных чисел.
является аналогом числа 1 во множестве действительных чисел.
Пусть имеем матрицу  . Если в ней поменять местами строки и столбцы, сохранив их порядок, то получим матрицу
. Если в ней поменять местами строки и столбцы, сохранив их порядок, то получим матрицу  , которую называют транспонированной для
, которую называют транспонированной для  .
.
|
|
|
Легко заметить следующие два свойства операции транспонирования матрицы:
1°. Если матрицу  транспонировать дважды, то в результате получим исходную матрицу
транспонировать дважды, то в результате получим исходную матрицу  :
:  .
.
2°. При транспонировании квадратной матрицы элементы главной диагонали не меняются.
Определение 4. Если квадратная матрица  совпадает со своей
совпадает со своей
транспонированной матрицей  , то ее называют
, то ее называют
симметрической.
Из определения симметрической матрицы видно, что ее элементы должны быть симметричны относительно главной диагонали. Например, матрица  является симметрической, а матрица
является симметрической, а матрица  - нет.
- нет.
Рассмотрим квадратную матрицу второго порядка  . Определителем этой матрицы называют число, обозначаемое
. Определителем этой матрицы называют число, обозначаемое  , или
, или  , или
, или  , полученное из элементов матрицы
, полученное из элементов матрицы  по следующему правилу:
по следующему правилу: 
 . Например, если
. Например, если  , то
, то 
 .
.
Рассмотрим теперь квадратную матрицу третьего порядка  . Определителем этой матрицы назовем число
. Определителем этой матрицы назовем число  .
.
 =
=  , или
, или
 (1)
(1)
Равенство (1) называют разложением определителя по элементам первой строки.
Выражения  ;
;  и
и  называют алгебраическими дополнениями элементов
называют алгебраическими дополнениями элементов  ,
,  и
и  соответственно. Таким образом, разложение определителя третьего порядка по элементам первой строки может быть записано в виде:
соответственно. Таким образом, разложение определителя третьего порядка по элементам первой строки может быть записано в виде:  .
.
Нетрудно заметить, что аналогичным образом определитель третьего порядка может быть разложен по элементам второй и третьей строк, а также по элементам первого, второго или третьего столбца.
Рассмотрим теперь квадратную матрицу  го порядка
го порядка  . Определителем такой матрицы, разложенным по
. Определителем такой матрицы, разложенным по  ой строке, назовем число
ой строке, назовем число
 , где
, где  - элементы
- элементы  ой строки, а
ой строки, а  - их алгебраические дополнения.
- их алгебраические дополнения.
Рассмотрим основные свойства определителей.
1). При умножении всех элементов любой строки матрицы  на некоторое число определитель исходной матрицы умножается на это число.
на некоторое число определитель исходной матрицы умножается на это число.
2). Определитель матрицы, содержащей нулевую строку, равен нулю.
3). При перестановке местами любых двух строк матрицы  без изменения остальных строк определитель меняет знак.
без изменения остальных строк определитель меняет знак.
4). Определитель матрицы, содержащей две одинаковые строки, равен нулю.
5). Определитель матрицы  не изменится, если к любой строке матрицы прибавить любую другую строку, умноженную на некоторое число.
не изменится, если к любой строке матрицы прибавить любую другую строку, умноженную на некоторое число.
6). Определитель произведения двух квадратных матриц одинакового порядка равен произведению определителей этих матриц.
|
|
|
7). При транспонировании квадратной матрицы ее определитель не меняется.
Определение 4. Квадратную матрицу  называют вырожденной
называют вырожденной
(невырожденной), если 
 .
.
Число  называют собственным числом матрицы
называют собственным числом матрицы  , если оно является корнем уравнения
, если оно является корнем уравнения  .
.
Лекция № 7 Элементарные преобразования матриц. Ранг матрицы. Матричная запись системы линейных уравнений. Решение систем линейных уравнений методом Крамера.
Пусть имеем матрицу  . Рассматривая элементы каждой строки как координаты
. Рассматривая элементы каждой строки как координаты  мерных векторов
мерных векторов  соответственно, матрицу
соответственно, матрицу  можно записать в виде матрицы-столбца
можно записать в виде матрицы-столбца  . Наибольшее число линейно независимых векторов во множестве {
. Наибольшее число линейно независимых векторов во множестве {  } называют строчным рангом матрицы
} называют строчным рангом матрицы  .
.
Если же в матрице  элементы каждого столбца рассматривать как координаты
элементы каждого столбца рассматривать как координаты  мерных векторов
мерных векторов  , то матрицу
, то матрицу  можно записать в виде матрицы-строки
можно записать в виде матрицы-строки  =(
=( ). Наибольшее число линейно независимых векторов во множестве {
). Наибольшее число линейно независимых векторов во множестве {  } называют столбцовым рангом матрицы
} называют столбцовым рангом матрицы  . Можно доказать, что строчный и столбцовый ранги любой матрицы равны. Их общее значение называют рангом матрицы
. Можно доказать, что строчный и столбцовый ранги любой матрицы равны. Их общее значение называют рангом матрицы  и обозначают символом
и обозначают символом  .
.
Однако находить ранг матрицы по определению часто бывает неудобно из-за трудоемкости. Обычно для определения ранга матрицы ее преобразовывают к ступенчатому виду, который сразу позволяет определить линейную зависимость или независимость ее строк или столбцов.
Матрицей ступенчатого вида называют матрицу  , обладающую свойством: если
, обладающую свойством: если  - первый ненулевой элемент
- первый ненулевой элемент  строки
строки  , то все элементы матрицы, стоящие ниже и левее
, то все элементы матрицы, стоящие ниже и левее  , равны нулю (т.е
, равны нулю (т.е 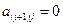 ,
,  при всех
при всех  ). При этом элементы
). При этом элементы  называют угловыми. Например, матрица
называют угловыми. Например, матрица  является матрицей ступенчатого вида. В первой строке первым отличным от нуля элементом является
является матрицей ступенчатого вида. В первой строке первым отличным от нуля элементом является  . Все элементы, стоящие ниже его равны нулю:
. Все элементы, стоящие ниже его равны нулю:  . Во второй строке первым отличным от нуля элементом является
. Во второй строке первым отличным от нуля элементом является  . Все элементы, стоящие ниже и левее равны нулю:
. Все элементы, стоящие ниже и левее равны нулю:  ,
,  . В третьей строке первый отличный от нуля элемент
. В третьей строке первый отличный от нуля элемент 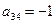 , а
, а  . В четвертой строке все элементы нулевые. Таким образом, угловыми элементами матрицы
. В четвертой строке все элементы нулевые. Таким образом, угловыми элементами матрицы  , имеющей ступенчатый вид, являются
, имеющей ступенчатый вид, являются  . Матрица
. Матрица  не является матрицей ступенчатого вида, так как для первого отличного от нуля элемента второй строки
не является матрицей ступенчатого вида, так как для первого отличного от нуля элемента второй строки  элемент
элемент  , стоящий ниже, отличен от нуля.
, стоящий ниже, отличен от нуля.
|
|
|
Рассмотрим преобразования, не меняющие ранга матрицы, т.е. не меняющие линейной зависимости (независимости) строк или столбцов матрицы. К ним относятся следующие преобразования, которые называют элементарными:
1) отбрасывание нулевой строки (столбца);
2) изменение порядка строк (столбцов);
3) транспонирование матрицы;
4) умножение всех элементов строки (столбца) на любое число  ;
;
5) умножение всех элементов одной строки (столбца) на любое число и прибавление их к соответствующим элементам другой строки (столбца).
Можно доказать, что с помощью перечисленных выше преобразований любая матрица приводится к ступенчатому виду. При этом ее ранг будет равен числу угловых элементов матрицы.
Систему, состоящую из  уравнений с
уравнений с  неизвестными
неизвестными  вида
вида
 (1)
(1)
называют системой линейных уравнений. В ней 
 - заданные числа. Решением такой системы называется набор чисел
- заданные числа. Решением такой системы называется набор чисел  , при подстановке которых в систему, каждое из уравнений превращается в верное равенство. Решить систему уравнений (1) – значит найти множество всех решений или доказать, что система не имеет решений. Система, имеющая хотя бы одно решение, называется совместной; в противном случае – несовместной.
, при подстановке которых в систему, каждое из уравнений превращается в верное равенство. Решить систему уравнений (1) – значит найти множество всех решений или доказать, что система не имеет решений. Система, имеющая хотя бы одно решение, называется совместной; в противном случае – несовместной.
Две системы линейных уравнений называют эквивалентными, если множества решений этих систем совпадают. В противном случае системы называют неэквивалентными.
Если  , то систему (1) называют однородной; в противном случае (т.е. если хотя бы одно из чисел
, то систему (1) называют однородной; в противном случае (т.е. если хотя бы одно из чисел  не равно нулю) – неоднородной.
не равно нулю) – неоднородной.
Матрицу  называют матрицей системы (1); матрицу
называют матрицей системы (1); матрицу  называют расширенной матрицей системы (1); матрицу
называют расширенной матрицей системы (1); матрицу  называют матрицей неизвестных, а матрицу
называют матрицей неизвестных, а матрицу  - матрицей свободных членов. Нетрудно заметить, что систему (1) можно записать в матричной форме в виде
- матрицей свободных членов. Нетрудно заметить, что систему (1) можно записать в матричной форме в виде
 . (2)
. (2)
Если в системе (1) число неизвестных совпадает с числом уравнений (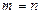 ) и
) и  , то систему можно решить методом Крамера по формулам
, то систему можно решить методом Крамера по формулам  ,
,  , …,
, …,  , где
, где  ,
,  определители, полученные из
определители, полученные из  заменой
заменой  го столбца столбцом свободных членов
го столбца столбцом свободных членов  .
.
Лекция № 8. Теорема Кронекера-Капели. Решение систем линейных уравнений методом Гаусса. Обратная матрица и способы ее нахождения. Матричный способ решения систем линейных уравнений.
Теорема (Кронекера – Капели) Чтобы система линейных уравнений была
совместной, необходимо и достаточно чтобы ранги основной и расширенной матриц были равны.
Общим способом решения системы линейных уравнений
 (1)
(1)
является метод Гаусса. Суть его состоит в том, чтобы данную систему линейных уравнений преобразовать к эквивалентной системе, максимально ее упростив. Можно показать, что такие преобразования как: перестановка местами любых двух уравнений в системе; умножение любого уравнения на любое число  ; умножение любого уравнения системы на любое число и прибавление его к любому другому уравнению системы, не изменяют множества решений системы, т.е. приводят к эквивалентной системе. Заметим, что перечисленные выше преобразования уравнений системы (1) фактически сводятся к элементарным преобразованиям матриц
; умножение любого уравнения системы на любое число и прибавление его к любому другому уравнению системы, не изменяют множества решений системы, т.е. приводят к эквивалентной системе. Заметим, что перечисленные выше преобразования уравнений системы (1) фактически сводятся к элементарным преобразованиям матриц  и
и  , из которых построена расширенная матрица системы (1). Поэтому преобразуем расширенную матрицу
, из которых построена расширенная матрица системы (1). Поэтому преобразуем расширенную матрицу  к ступенчатому виду. В результате преобразований возможны следующие три случая.
к ступенчатому виду. В результате преобразований возможны следующие три случая.
|
|
|
1) При некотором преобразовании получаем строку матрицы, в которой все элементы до черты равны нулю, а элемент после черты отличен от нуля. Это говорит о том, что в системе есть уравнение
 ,
,  ,
,
которое не имеет решений. Следовательно, в этом случае система несовместна.
2) После отбрасывания нулевых строк, если таковые есть, получим квадратную матрицу треугольного вида  . В ней
. В ней  . По этой матрице можно записать систему уравнений, равносильную системе (1). Она имеет вид
. По этой матрице можно записать систему уравнений, равносильную системе (1). Она имеет вид  .
.
Из последнего уравнения находим  . Подставляя это значение
. Подставляя это значение 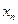 в предпоследнее уравнение, найдем
в предпоследнее уравнение, найдем  . Затем, подставив найденные значения
. Затем, подставив найденные значения 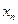 и
и  в предыдущее уравнение, получим
в предыдущее уравнение, получим  . Продолжая далее этот процесс, получим
. Продолжая далее этот процесс, получим  .
.
Таким образом, в этом случае система (1) имеет единственное решение. Такие системы называют определенными.
3) После отбрасывания нулевых строк, если таковые есть, получим матрицу ступенчатого вида  . По этой матрице можно записать систему уравнений, равносильную системе (1). Она имеет вид
. По этой матрице можно записать систему уравнений, равносильную системе (1). Она имеет вид
 .
.
Не ограничивая общности можно считать, что  . Выразив из последнего уравнения системы
. Выразив из последнего уравнения системы  через
через  , получим
, получим  . Затем подставим найденное значение
. Затем подставим найденное значение  в предыдущее уравнение и выразим
в предыдущее уравнение и выразим  через
через  . Подставив
. Подставив  в предыдущее уравнение, выразим
в предыдущее уравнение, выразим  через
через  . И так далее. После
. И так далее. После  шагов мы выразим
шагов мы выразим  через
через  и получим общее решение системы (1). Ясно, что в общем решении содержится бесконечно много решений системы (1), так как переменные
и получим общее решение системы (1). Ясно, что в общем решении содержится бесконечно много решений системы (1), так как переменные  могут принимать любые значения. Их называют свободными переменными. Придавая свободным переменным конкретные значения мы будем получать различные частные решения системы (1). Системы уравнений, имеющие бесконечно много решений, называют неопределенными.
могут принимать любые значения. Их называют свободными переменными. Придавая свободным переменным конкретные значения мы будем получать различные частные решения системы (1). Системы уравнений, имеющие бесконечно много решений, называют неопределенными.
Легко видеть, что если система (1) является однородной, то она всегда совместна, так как имеет решение  . В этом случае никакое из элементарных преобразований не меняет матрицу свободных членов
. В этом случае никакое из элементарных преобразований не меняет матрицу свободных членов  . Поэтому при решении однородных систем методом Гаусса обычно приводят к ступенчатому виду матрицу системы, а не расширенную матрицу системы.
. Поэтому при решении однородных систем методом Гаусса обычно приводят к ступенчатому виду матрицу системы, а не расширенную матрицу системы.
Пусть имеем квадратную матрицу  . Обратной для нее называют такую матрицу
. Обратной для нее называют такую матрицу  , которая удовлетворяет условию
, которая удовлетворяет условию 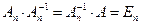 .
.
Легко заметить, что не всякая матрица имеет обратную. Действительно, по свойству определителей с учетом определения обратной матрицы должны иметь  . А поскольку
. А поскольку  , то ни один из определителей
, то ни один из определителей  и
и  не может равняться нулю. Значит необходимым условием существования обратной матрицы для матрицы
не может равняться нулю. Значит необходимым условием существования обратной матрицы для матрицы  является ее невырожденность. Можно доказать, что это условие является и достаточным. Для этого просто укажем алгоритм получения обратной матрицы для любой невырожденной матрицы
является ее невырожденность. Можно доказать, что это условие является и достаточным. Для этого просто укажем алгоритм получения обратной матрицы для любой невырожденной матрицы  .
.
1) Вычисляем  .
.
2) Для каждого элемента матрицы  вычисляем алгебраические дополнения
вычисляем алгебраические дополнения  .
.
3) Составляем из этих алгебраических дополнений матрицу  .
.
4) Транспонируем матрицу  , получая матрицу
, получая матрицу  , называемую присоединенной к матрице
, называемую присоединенной к матрице  .
.
5) Умножаем матрицу  на число
на число  .
.
Полученная в результате матрица 
 и будет обратной для
и будет обратной для  . В этом можно убедиться проверкой.
. В этом можно убедиться проверкой.
Существует другой способ нахождения обратной матрицы – способ перегонки. Суть его в следующем. Пусть имеем невырожденную квадратную матрицу 
 . Припишем к данной матрице
. Припишем к данной матрице  справа единичную матрицу
справа единичную матрицу  , т.е. построим матрицу
, т.е. построим матрицу  и с помощью элементарных преобразований над матрицами «перегоним» матрицу
и с помощью элементарных преобразований над матрицами «перегоним» матрицу  , стоящую справа от черты, на место матрицы
, стоящую справа от черты, на место матрицы  , стоящей слева от черты. Тогда матрица, получившаяся справа от черты и будет обратной для
, стоящей слева от черты. Тогда матрица, получившаяся справа от черты и будет обратной для  . В этом можно убедиться проверкой.
. В этом можно убедиться проверкой.
Если в системе (1) число уравнений совпадает с числом неизвестных  , а матрица системы
, а матрица системы  является невырожденной, то кроме метода Гаусса можно также применить матричный метод. Суть его состоит в следующем. Находим матрицу
является невырожденной, то кроме метода Гаусса можно также применить матричный метод. Суть его состоит в следующем. Находим матрицу  , обратную для матрицы
, обратную для матрицы  , и умножаем ее слева на матричное уравнение системы. Получаем
, и умножаем ее слева на матричное уравнение системы. Получаем  . Учитывая, что
. Учитывая, что  , а
, а  , приходим к уравнению
, приходим к уравнению  , которое и дает нам искомое решение (в матричном виде). Очевидно, что этот метод можно применять только для решения систем с невырожденной матрицей. В противном случае для матрицы
, которое и дает нам искомое решение (в матричном виде). Очевидно, что этот метод можно применять только для решения систем с невырожденной матрицей. В противном случае для матрицы  нет обратной.
нет обратной.
|
|
|


