 |
Некоторые задачи анализа опытных данных
|
|
|
|
Интерполирование. Под интерполированием понимают, во-первых, нахождение значений функции для промежуточного значений аргумента, отсутствующих в таблице и, во-вторых, замену функции интерполирующим многочленом, если аналитическое выражение ее неизвестно, а функция должна подвергаться определенным математическим операциям. Наиболее простые способы интерполирования – линейное и графическое. Линейное интерполирование можно применять тогда, когда зависимость у (х) выражается прямой линией или кривой, близкой к прямой, для которой такое интерполирование не приводит к грубым погрешностям. В некоторых случаях можно проводить линейное интерполирование и при сложной зависимости у (х), если оно ведется в пределах настолько малого изменения аргумента, что зависимость между переменными можно считать линейной без заметных погрешностей. При графическом интерполировании неизвестную функцию у (х) заменяют ее приближенным графическим изображением (по экспериментальным точкам или табличным данным), из которого определяют значения у при любых х в пределах измерений. Однако точное графическое построение сложных кривых иногда оказывается очень трудным, например кривой с резкими экстремумами, поэтому графическое интерполирование имеет ограниченное применение.
Таким образом, во многих случаях невозможно применить ни линейного, ни графического интерполирования. В связи с этим были найдены интерполирующие функции, позволяющие вычислить значения у с достаточной точностью для любой функциональной зависимости у (х) при условии, что она является непрерывной. Интерполирующая функция имеет вид
, (7.1)
|
|
|
где B 0, B 1, … Bn – определяемые коэффициенты. Так как данный многочлен (7.1) изображается кривой параболического типа, то такая интерполяция называется параболической.
Коэффициенты интерполирующего многочлена находят, решая систему из (l + 1) линейных уравнений, получающихся при подстановке в уравнение (7.1) известных значений у i и х i.
Наиболее просто производится интерполирование, когда интервалы между значениями аргумента постоянны, т. е.
, (7.2)
где h – постоянная величина, называемая шагом. В общем случае
. (7.3)
При использовании интерполяционных формул приходится иметь дело с разностями значений у и разностями этих разностей, т. е. разностями функции у (х) различных порядков. Разности любого порядка вычисляются по формуле
. (7.4)
Например,
и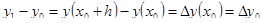 
.
При вычислении разностей их удобно располагать в виде таблицы (см. Табл. 4), в каждом столбце которой разности записывают между соответствующими значениями уменьшаемого и вычитаемого, т. е. составляется таблица диагонального типа. Обычно разности записывают в единицах последнего знака.
Таблица 4
Разности функции у (х)
| x | y | Dy | D2y | D3y | D4y |
| x0 | у0 | Dу0 Dу1 Dу2 Dу3 | D2у0 D2у1 D2у2 | ||
| x1 | у1 | D3у0 D3у1 | |||
| x2 | у2 | D4у0 | |||
| x3 | у3 | ||||
| х4 | у4 |
Так как функция у (х) выражается многочленом (7.1) n -ой степени относительно х, то разности также являются многочленами, степени которых понижаются на единицу при переходе к последующей разности. N -я разность многочлена n -ой степени является постоянным числом, т. е. содержит х в нулевой степени. Все разности более высокого порядка равны нулю. Это определяет степень интерполирующего многочлена.
Преобразовав функцию (7.1), можно получить первую интерполяционную формулу Ньютона:
|
|
|
. (7.5)
Она используется для нахождения значений у при любых х в пределах измерений. Представим эту формулу (7.5) в несколько ином виде:
. (7.6)
Последние две формулы иногда называют интерполяционными формулами Ньютона для интерполирования вперед. В эти формулы входят разности, идущие по диагонали вниз, и их удобно использовать в начале таблицы экспериментальных данных, где разностей достаточно.
Вторая интерполяционная формула Ньютона, выведенная из того же уравнения (7.1), выглядит следующим образом:
. (7.7)
Данную формулу (7.7) принято называть интерполяционной формулой Ньютона для интерполирования назад. Она используется для определения значений у в конце таблицы.
Теперь рассмотрим интерполяцию при неравноотстоящих значениях аргумента.
Пусть по-прежнему функция у (х) задается рядом значений хi и уi, но интервалы между последовательными значениями хi неодинаковы. Использовать вышеприведенные формулы Ньютона нельзя, так как они содержат постоянный шаг h. В задачах такого рода необходимо вычислить приведенные разности:
; 
и т. д.
; 
и т. д. (7.8)
Разности более высоких порядков вычисляются аналогично. Как и для случая равноотстоящих значений аргумента, если f (х) – многочлен n -ой степени, то разности n -го порядка постоянны, а разности более высокого порядка равны нулю. В простых случаях таблицы приведенных разностей имеют вид, аналогичный таблицам разностей при равноотстоящих значениях аргумента.
Помимо рассмотренных интерполяционных формул Ньютона часто применяют интерполяционную формулу Лагранжа:
. (7.9)
В этой формуле каждое из слагаемых представляет собой многочлен n -ой степени и все они равноправны. Поэтому до окончания вычислений нельзя пренебрегать какими-либо из них.
Обратное интерполирование. На практике иногда бывает необходимо найти значение аргумента, которому соответствует определенное значение функции. В этом случае интерполируют обратную функцию и следует иметь в виду, что разности функции не постоянны и интерполирование нужно проводить для неравноотстоящих значений аргумента, т. е. использовать формулу (7.8) или (7.9).
|
|
|
Экстраполирование. Экстраполированием называют вычисление значений функции у за пределами интервала значений аргумента х, в котором были проведены измерения. При неизвестном аналитическом выражении искомой функции экстраполирование нужно проводить весьма осторожно, так как не известно поведение функции у (х) за пределами интервала измерений. Экстраполяция допускается, если ход кривой плавный и нет причин ждать резких изменений в исследуемом процессе. Тем не менее экстраполирование должно проводиться в узких пределах, например в пределах шага h. В более далеких точках можно получить неверные значения у. Для экстраполирования применяются те же формулы, что и для интерполирования. Так, первая формула Ньютона используется при экстраполировании назад, а вторая формула Ньютона – при экстраполировании вперед. Формула Лагранжа применяется в обоих случаях. Надо также иметь в виду, что экстраполирование приводит к большим погрешностям, чем интерполирование.
Численное интегрирование.
Формула трапеций. Формулу трапеций обычно применяют в том случае, если значения функции измерены для равноотстоящих значений аргумента, т. е. с постоянным шагом. По правилу трапеций в качестве приближенного значения интеграла
(7.10)
принимают величину
, (7.11)
Рис. 7.1. Сравнение методов численного интегрирования
т. е. полагают 
. Геометрическая интерпретация формулы трапеций (см. рис. 7.1) следующая: площадь криволинейной трапеции заменяется суммой площадей прямолинейных трапеций. Полная ошибка вычисления интеграла по формуле трапеций оценивается как сумма двух ошибок: ошибки усечения, вызванной заменой криволинейной трапеции прямолинейными, и ошибки округления, вызванной ошибками измерения значений функции. Ошибка усечения для формулы трапеций составляет
, где 
. (7.12)
Формулы прямоугольников. Формулы прямоугольников, как и формулу трапеций применяют также в случае равноотстоящих значений аргумента. Приближенная интегральная сумма определяется по одной из формул
|
|
|
, (7.13)
. (7.14)
Геометрическая интерпретация формул прямоугольников дана на рис. 7.1. Погрешность формул (7.13) и (7.14) оценивается неравенством
, где 
. (7.15)
Формула Симпсона. Приближенно интеграл определяется по формуле
, (7.16)
где n – четное число. Ошибка формулы Симпсона оценивается неравенством
, где 
. (7.17)
Формула Симпсона приводит к точным результатам для случая, когда подынтегральная функция является многочленом второй или третьей степени.
Численное интегрирование дифференциальных уравнений. Рассмотрим обыкновенное дифференциальное уравнение первого порядка у ' = f (х, у) с начальным условием у = у 0 при х = х 0. Требуется найти приближенно его решение у = у (х) на отрезке [ х 0, х k ].
Рис. 7.2. Геометрическая интерпретация метода Эйлера
Для этого данный отрезок делится на n равных частей длиной (х k – х 0)/ n. Поиск приближенных значений у 1, у 2, …, у n функции у (х) в точках деления х 1, х 2, …, х n = х k осуществляется различными методами.
Метод ломаных Эйлера. При заданном значении у 0 = у (х 0) остальные значения у i 
у (х i) последовательно вычисляются по формуле
, (7.18)
где i = 0, 1, …, n – 1.
Графически метод Эйлера представлен на рис. 7.1, где график решения уравнения у = у (х) приближенно представляется ломаной (откуда и происходит название метода). Метод Рунге-Кутта. Обеспечивает более высокую точность по сравнению с методом Эйлера. Искомые значения у i последовательно вычисляются по формуле
, (7.19), где 
,
, 
, 
.
ОБЗОР НАУЧНОЙ ЛИТЕРАТУРЫ
Обзор литературы – обязательная часть всякого отчета об исследовании. Обзор должен полно и систематизированно излагать состояние вопроса, позволять объективно оценивать научно-технический уровень работы, правильно выбирать пути и средства достижения поставленной цели и оценивать как эффективность этих средств, так и работы в целом. Предметом анализа в обзоре должны быть новые идеи и проблемы, возможные подходы к решению этих проблем, результаты предыдущих исследований, данные экономического характера, возможные пути решения задач. Противоречивые сведения, содержащиеся в различных литературных источниках, должны быть проанализированы и оценены с особой тщательностью.
Из анализа литературы должно быть видно, что в этом узком вопросе известно вполне достоверно, что сомнительно, спорно; какие задачи в поставленной технической проблеме первоочередные, ключевые; где и как стоит искать их решения.
|
|
|
Затраты времени на обзор складываются примерно так:
| выписки из справочников, чтение и конспектирование основных монографий | 3 – 5 % |
| составление рабочего плана обзора | 1 – 2 % |
| поиск периодики (и составление картотеки или списка литературы) | 5 – 8 % |
| чтение и конспектирование периодики | 30 – 40 % |
| отбор материала из конспектов, его сопоставление и анализ | 20 – 30 % |
| написание обзора | 10 – 20 % |
| правка текста | 10 – 15 % |
| переписка и изготовление рисунков | 5 – 6 % |
Исследование всегда имеет узкую конкретную цель. В заключении обзора обоснованы выбор цели и метода. Обзор должен подготовить это решение. Отсюда следует его план и отбор материала. В обзоре рассматривают только такие узкие вопросы, которые могут прямо повлиять на решение задачи, но настолько полно, чтобы охватить практически всю современную литературу по этому вопросу.
|
|
|
