Монополистическая конкуренция

Составитель А.Л. ДМИТРИЕВ

 

САНКТ-ПЕТЕРБУРГ

 

 

© А.Л. Дмитриев, 2013

 

Измерение концентрации рынка

№ 1. Ниже приведены данные о мощности крупнейших энергетических компаний региона (в млн. кВт).

А 57,439

Б 12,914

В 1,136

Г 5,351

Д 8,113

Е 1,827

Ж 0,16

И 0,59

Рассчитать показатели концентрации рынка: индекс концентрации для 3-х и 4-х компаний, индекс Херфиндаля-Хиршмана, дисперсию рыночных долей, индекс энтропии и построить кривую Лоренца.

№ 2. На основе приведенных данных о долях продаж на рынках А и Б и ценовой эластичности спроса рассчитать индекс Херфиндаля-Хиршмана и индекс Лернера для двух рынков при условии, что на первом коэффициент ß составляет 0,5, а на втором – 0,05.

Рынок А Рынок Б

Эластичность спроса –4 Эластичность спроса –1,5

Фирма Доля Фирма Доля

1 60 1 30

2 30 2 25

3 5 3 25

4 5 4 20

 

№ 3. На рынке некоторого товара действует 4 фирм. Каждая из них контролирует по 25 процентов рынка. Пакеты акций этих фирм можно продать вдвое дороже номинала. Акционерный капитал каждой компании составляет 100 млн. долл. Прибыль – 25%. Нормальная прибыль для отрасли 10% на акционерный капитал. Эластичность рыночного спроса –1,5.

Рассчитать показатели монопольной власти: индекс Бейна, индекс Тобина, индекс Лернера.

№ 4. На рынке действуют 5 фирм, данные об объемах продаж, ценах и предельных затратах приведены в таблице.

Фирма Объем продаж, тыс. шт Предельные затраты, тыс. долл.

А 1350 3,55

Б 1125 3,625

В 900 3,7

Г 675 3,775

Д 450 3,85

Цена товара 5 тыс. долл. Определить коэффициента бета и эластичность спроса по цене.

 

№ 5. Информация о фирмах и их рангах представлена в таблице. Рассчитать индекс Холла-Тайдмана и сделать выводы:

Фирма	Выпуск в 2008 г.	Ранг в 2008 г.	Выпуск в 2009 г.	Ранг в 2009 г.
А
Б
В
Г
Д
Е
Ж
З

 

№ 6. Имеется информация о выпуске компаний, действующих на рынке. Рассчитать индекс Линда и определить нарушение непрерывности.

Фирма	Выпуск, шт.
А
Б
В
Г
Д
Е
Ж
З
Итого

 

Альтернативные цели фирмы

№ 7. При фиксированном количестве применяемого труда выпуск монополии характеризуется производственной функцией: Q = 2K, где K – количество капитала. Функция затрат монополии имеет вид: TC = 50 + Q + Q², а функция спроса на ее продукцию: Q = 200 – P. Определить объем выпуска монополии когда она стремится максимизировать: а) прибыль, б) выручку, в) среднюю норму прибыли.

№ 8. Производственная функция фирмы имеет вид: Q = 40 L – L ². Постоянные издержки фирмы равны 10. Определить при P = 2 объем продаж, число занятых и ATC, если фирмы а) максимизирует прибыль (w = 20), б) управляется работниками и максимизирует чистую выручку на одного занятого, в) управляется менеджерами, стремящимися максимизировать выплаты административно-управленческому персоналу (I). Зависимость выплат имеет вид: I (π, L) = 10 + 0.1 π + L. Построить функцию предложения фирмы, если она совершенный конкурент и сравнить ее с функцией предложения для фирмы, управляемой работниками.

Что произойдет, если постоянные затраты возрастут до 20?

 

№ 9. Производственная функция имеет вид: Q = L ^0,6; а цены P = 4; r = 1; w = 0,2, количество капитала K = 4. Определить параметры фирмы (прибыль, объем продаж, величину труда) если она – конкурент, максимизирующий прибыль и коллективное предприятие. Рассчитать те же параметры если а) цена блага увеличилась до 6; б) цена труда возросла до 0,4.

Монополия

№ 10. Функция общих затрат фирмы имеет вид:

TC = 30000 + 50Q. Цена на ее продукцию меняется по формуле: P = 100 – 0,01Q.

а) Определить цену, при которой фирма получит максимум прибыли, и размер этой прибыли.

б) Определить те же параметры, если фирма должна будет уплачивать налог в размере 10 ден. ед. с каждой реализованной единицы продукции.

в) Определить те же параметры, если фирма должна уплачивать налог на капитал в размере 200 ден. ед.

№ 11. Функция спроса на продукцию монополии имеет вид: Q = 400/P, а функция общих затрат монополии: TC = 5 Q + 0,25 Q ². Как изменится цена на данном рынке, если за каждую проданную единицу товара монополия будет получать дотацию в размере 2 ден. ед?

№ 12. Даны функции общих затрат двух заводов монополии TC ₁ = =10 Q ₁ + 5; TC₂ = 2 Q ₂² + 60. Функция спроса на продукцию монополии имеет вид Q = 360 – 2 P. Определить общий выпуск и цену, максимизирующие прибыль. Как распределится выпуск по двум заводам?

№ 13. Монополия владеет двумя предприятиями, функции затрат которых даны: TC₁ = 10Q₁, TC₂ = 0,25 Q₂ ². Функция спроса на продукцию: Q = 200 – 2 P. Определить оптимальную для монополии цену, объемы производства на каждом предприятии и сумму прибыли.

 

№ 14. Известны функция спроса на продукцию монополии Q^D = 120 – 4 P, и функция ее затрат TC = 220 + 3 Q + 0,125 Q ². Определить:

а) На сколько больше прибыли получит монополия при стремлении к максимуму прибыли по сравнению со стремлением к максимуму выручки?

б) На сколько возрастут излишки потребителей при стремлении монополии к максимуму выручки по сравнению со стремлением к максимуму прибыли?

 

№ 15. При максимизации прибыли монополия с функцией общих затрат: TC = 100 +2 Q + 0,5 Q ² продает 10 ед. продукции, а при максимизации выручки 16 ед. С каждой единицей проданной продукции монополия платит акциз в размере 5 ден. ед. Сколько ед. продукции будет продано при максимизации прибыли монополии?

 

№ 16. Товар производится по технологии, отображающейся производственной функцией Q = L ^0,8 K ^0,2, а рыночный спрос – функцией Q^D = 40 – 2 P. В условиях совершенной конкуренции на рынке продается 36 ед. товара. На сколько сократятся излишки покупателей, если на этом рынке возникнет монополия, максимизирующая прибыль?

 

№ 17. При линейной функции спроса монополия получает максимум прибыли, продавая 12 ед. продукции по цене 40 ден. ед. Функция общих затрат монополии

TC = 50 + 10 Q + 0,5 Q ².

а) Насколько возрастут суммарные излишки производителей и потребителей, если при тех же затратах продукция будет продаваться в условиях совершенной конкуренции?

б) Насколько снизится цена монополии, если за каждую проданную единицу продукции ей доплачивать 5 ден. ед?

в) Насколько с учетом дотации увеличится прибыль монополии?

№ 18. Отраслевой спрос Q^D = 180 – 2 P удовлетворяет единственная фирма с функцией общих затрат: TC = 120 + 12 Q + 0,5 Q ².

1. Определите цену и объем продаж, если фирма максимизирует: а) прибыль; б) выручку; в) объем продаж.

2. Насколько максимальная прибыль превышает прибыль при максимизации объема продаж?

3. Определите величину дотации за каждую проданную единицу товара, при которой фирма, стремясь максимизировать прибыль, будет продавать 45 ед.

4. Определите цену и объем продаж, если фирма максимизирует при наличии 20%-го налога на выручку.

№ 19. Даны функция затрат монополии и функция спроса: TC = 50 + 20Q, P = 100 – 4Q. Определить объем производства, цену и сумму максимальной прибыли монополии. Как изменится объем производства и сумма прибыли, если монополия будет осуществлять совершенную ценовую дискриминацию?

 

№ 20. Дана функция спроса монополии: Q = 180 – 2P. Функция общих затрат имеет следующий вид: TC = 2Q² + 90. Определить объем выпуска и цену, максимизирующие прибыль монополии. Определить объем выпуска, если монополист получит возможность применять совершенную ценовую дискриминацию.

 

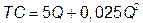№ 21. Спрос на продукцию монополии отображается функцией , а ее затраты − функцией . Монополия может проводить ценовую дискриминацию 2-й степени при условии, что 1-я партия продукции состоит из 25 ед. Определить:

а) Какую максимальную прибыль может получить монополия в этом случае?

б) Насколько возросла бы прибыль монополии, если бы она могла проводить ценовую дискриминацию 1-й степени?

 

№ 22. Функция спроса на продукцию монополии имеет вид: Р = 24 –1,5 Р. Общие затраты монополии ТС = 50 + 0,1 Q ². Определить максимально возможный объем прибыли монополии при продаже всей продукции по единой цене и при продаже выпуска партиями, первая из которых содержит 3 шт.

 

№ 23. Монополия, максимизирующая прибыль, может продавать продукцию на двух сегментах рынка, имеющих следующие функции спроса q ₁ = 100 – 2 P ₁и q ₂ = 60 – 2 P ₂. Функция общих затрат монополии имеет вид: TC = 14 Q;

q ₁ + q ₂ = Q. Определить:

а) Какими будут цены, объемы продаж и прибыль монополии при использовании ценовой дискриминации?

б) Какими будут цена, объем выпуска и прибыль монополии при отсутствии условий для ценовой дискриминации?

 

№ 24. Монополия может продавать продукцию на двух сегментах рынка с различной эластичностью спроса:

= 200 – 4 P _1; = 160 – 2 P ₂. Ее функция общих затрат TC = 10 + 12 Q + 0,5 Q ². Определить:

а) При каких ценах на каждом из сегментов рынка монополия получит максимум прибыли?

б) Какую цену установит монополия в случае запрета ценовой дискриминации?

 

№ 25. Потребности жителей города в молоке отображаются функцией Q^D = 280 – 4 P и удовлетворяются одним заводом с функцией общих затрат TC = 100 + 10 Q + 0,25 Q ². Половина жителей города – дети. За каждый проданный детям литр молока муниципалитет платит заводу 10 ден. ед. Определить:

а) Как молокозаводу распределить свой выпуск между детьми и взрослыми, чтобы получить максимум прибыли?

б) Какая цена будет установлена для детей и для взрослых?

в) Насколько меньше молока производил бы завод без дотации?

№ 26. Спрос на продукцию монополии, максимизирующей прибыль, отображается функцией Q^D = 240 – 4 P; функция общих затрат TC = 120 + 10 Q + Q ². Насколько изменится выпуск монополии, если установить верхний предел цены: а) Р = 52; б) Р = 50; в) Р = 48.

 

№27. Функция спроса на продукцию естественной монополии: Q^D = 6 – 0,1 P; функция общих затрат TC = 48 Q + 12 Q ² + Q ³. Определить:

а) Сумму дотации монополии, чтобы она могла работать безубыточно при директивной цене Р = МС.

б) Насколько меньше был бы выпуск монополии без государственного регулирования цены?

в) Какую минимальную директивную цену можно установить, чтобы монополия могла работать безубыточно без дотации?

 

№ 28. На рынке два типа покупателей – А и Б. Функция спроса группы А имеет вид: P₁ = 20 – q₁, а группы Б: P₂ = 4 – q₂. Всего на рынке 100 покупателей, причем группы А – 60, а группы Б – 40. Средние издержки на производство товара (AC) равны 2. Рассчитать двухчастный тариф по двум схемам и определить величину прибыли в двух случаях.

 

 

№29. Спрос на продукцию отображается функцией Q^D = 140 – 4 P, а общие затраты на ее производство – функцией TC = 80 + 5 Q + Q ². Продукция продается на рынке совершенной конкуренции. Во сколько раз должны снизиться переменные затраты, чтобы при переходе от совершенной конкуренции к монополии цена не изменилась?

№ 30. В регионе имеется единственное овощехранилище, закупающее картофель у 100 фермеров, выращивающих картофель с одинаковыми затратами TC_i = 2 + + 0,25 q ² _i, где q_i – количество картофеля, выращенного i -м фермером. Хранилище сортирует и фасует картофель по технологии, отображаемой производственной функцией Q_f = 8 Q ^0,5, где Q_f – количество расфасованного картофеля; Q = S q_i – количество закупленного картофеля. Определите суммарную прибыль фермеров при стремлении овощехранилища к максимуму прибыли, если: а) оно может продавать любое количество картофеля по фиксированной цене P_f = 20; б) спрос на фасованный картофель отображается функцией .

 

№ 31. В городе имеется единственный элеватор, закупающий зерно у двух групп фермеров, различающихся затратами: и , где q_i – количество зерна произведенного одним фермером i –й группы. В первой группе 40 фермеров, во второй – 20. Элеватор производит муку по технологии, отображаемой производственной функцией Q_z = 8 Q ^0,5, где Q_z – количество муки; Q = S q_i – количество закупленного зерна, и может продавать любое количество муки по фиксированной цене P_z = 16. При закупке сырья молокозавод может проводить ценовую дискриминацию. Насколько больше прибыли получит элеватор при проведении ценовой дискриминации по сравнению с закупкой зерна по единой цене?

 

№ 32. Спрос на продукцию монополии отображается функцией . Монополия может производить продукцию на двух предприятиях, различающихся функциями затрат: 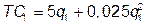и ; q ₁ + q ₂ = Q. Как распределить выпуск между предприятиями, чтобы прибыль была максимальной?

 

 

Монополистическая конкуренция

 

№ 33. Монополистический конкурент, производящий продукцию с затратами: TC = 9,5Q, установил, что цена на его продукцию меняется по формуле: P = 23,5 – 0,5Q, если он продает больше 11, по формуле: P = 25 – 1/3 Q, если он продает не больше 6 ед., по формуле: P = 29 – Q, если он продает больше 6, но не больше 11 ед. Определить объем выпуска данной фирмы, максимизирующий прибыль, и размер этой прибыли.

 

№ 34. Функция спроса на продукцию фирмы имеет вид:

а функция общих затрат TC = 50 + 12 Q + 0,125 Q ².

1. При какой цене прибыль фирмы максимальна?

2. Насколько изменится цена при взимании акциза в размере 2 ден. ед. с каждой проданной единицы продукции?

3. Насколько изменится цена при предоставлении дотации в размере 1 ден. ед. за каждую проданную единицу продукции?

4. Определите максимум прибыли при TC = 500 + 0,05 Q ².

 

№ 35. Монополистический конкурент с функцией общих затрат TC = 300 + 30 Q + 2 Q ² в состоянии длительного равновесия производит продукцию со средними затратами на 21 ден. ед. больше, чем минимально возможные.

1. Определите цену и объем продаж данной фирмы.

2. Насколько больше продавала бы каждая фирма, если бы вследствие стандартизации продающегося на рынке продукта монополистическая конкуренция сменилась совершенной конкуренцией?

 

№ 36. Когда фирма с функцией затрат TC = 128 + 10 Q + 0,5 Q ² на рынке монополистической конкуренции достигла долгосрочного равновесия, коэффициент эластичности спроса по цене на ее товар e^D = –2,5. Сколько единиц товара продавала фирма?

№ 37. Монополистический конкурент с функцией общих затрат TC = 300 + 10 Q + 0,5 Q ² в состоянии длительного равновесия продает свою продукцию по цене Р = 45. До прихода в отрасль новых конкурентов он мог по каждой цене продавать на 12 ед. своей продукции больше. Какова тогда была его прибыль?

 

№ 38. Текущий спрос на продукцию монополистического конкурента отображается функцией , а общие затраты . Изменение числа конкурентов в отрасли смещает кривую спроса на продукцию фирмы без изменения ее наклона. На сколько сократится прибыль данной фирмы в состоянии длительного равновесия по сравнению с текущим периодом?

№ 39. В данный момент спрос на продукцию монополистического конкурента отображается функцией , а общие затраты .

Изменение числа конкурентов в отрасли смещает кривую спроса на продукцию фирмы без изменения ее наклона. Насколько в состоянии длительного равновесия: а) снизятся цена и выпуск данной фирмы по сравнению с текущим моментом; б) средние затраты превышают минимально возможные?

 

№ 40. Известны функция спроса на продукцию монополистического конкурента Q_A = 30 – 5P_A + 2 P_B и функция затрат TC_A = 24 +3Q_A. Определить цены двух благ после установления отраслевого равновесия в длительном периоде.

 

Олигополия

 

№ 41. Отраслевой спрос задан функцией цены спроса P = 200 – Q; в отрасли работают две максимизирующие прибыль фирмы I иII со следующими функциями затрат: TC _I = 100 + 0,5 q² _I и TC _II= 50 + 40 q _II. Определите прибыль каждой фирмы в соответствии с: а) моделью Курно; б) моделью Штакельберга при лидерстве фирмы I; в) картельным соглашением при распределении прибыли пропорционально выпуску.

 

№ 42. Отраслевой спрос Q^D = 120 – 2 P удовлетворяет монополия, максимизирующая прибыль и имеющая неизменные средние затраты. Она установила цену Р = 40. Еще одна фирма с функцией затрат ТС = 0,25 q ² вошла в отрасль. На сколько единиц сократится выпуск бывшей монополии после установления долгосрочного равновесия в отрасли в соответствии с моделью дуополии Курно?

№ 43. Отраслевой спрос на рынке дуополии представляет функция Q^D = 70 – 0,5 P; обе фирмы имеют одинаковые затраты: TC_i = 20 + q ² _i. Насколько снизится цена и насколько возрастет объем продаж, если фирмы перейдут от поведения в соответствии с моделью Курно к поведению в соответствии с моделью Штакельберга?

 

№ 44. Отраслевой спрос Q^D = 80 – 2 P удовлетворяет монополия, максимизирующая прибыль и имеющая неизменные средние затраты. Она установила цену Р = 25. Еще одна фирма с функцией затрат ТС = 0,25 q ² вошла в отрасль, согласившись на роль последователя. Насколько единиц сократится выпуск бывшей монополии после установления долгосрочного равновесия в отрасли в соответствии с моделью дуополии Штакельберга?

№ 45. На рынке дуополии спрос существует только при Р < 50 и достигает полного удовлетворения при Q = 200. Известны уравнения реакции обоих дуополистов, ведущих себя в соответствии с моделью Курно: q ₁ = 60 – 0,25 q ₂; q ₂ = 100 – 0,5 q ₁. Какая цена установится на рынке?

№ 46. В отрасли функционируют 120 мелких фирм с одинаковыми функциями затрат TC_i = 20 + 10 и еще одна крупная фирма, выступающая в роли лидера, с функцией затрат TC _л = 50 + 0,5 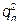. Отраслевой спрос отображается функцией Q^D = 400 – 2 P.

1. Определите прибыль лидера и каждого из аутсайдеров.

2. Вследствие увеличения доходов покупателей они стали спрашивать на 40 ед. товара больше. Насколько возрастет объем продаж и как прирост выпуска распределится между лидером и аутсайдерами?

№ 47. Отраслевой спрос отображается функцией Q^D = 256 – 3 P. В отрасли функционируют одна крупная фирма, выступающая в роли лидера, с функцией затрат TC _л = 50 + 0,25 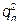и мелкие фирмы-аутсайдеры с одинаковыми функциями затрат TC_i = 2 + 15 . Лидер установил цену Р = 60 и продает 20 ед. продукции. Сколько аутсайдеров работает в этой отрасли?

 

№ 48. На рынке совершенной конкуренции с отраслевым спросом торговали фирмы с одинаковыми затратами . В определенный момент 20 фирм образовали картель, став ценовым лидером.

1. Насколько в результате этого возросла цена и сократился объем продаж?

2. Насколько бы возросла цена и сократился объем продаж, если бы в картель вошли 30 фирм?

№ 49. На рынке с отраслевым спросом Q^D = 120 – P установилась монопольная цена вследствие того, что продавцы образовали картель с общими затратами TC = 450 + 12 Q + Q ². После того, как руководству картеля стало известно, что еще одна фирма с такими же общими затратами намеревается войти в отрасль, картель решил снизить цену на столько, чтобы у потенциального конкурента исчезло желание входить в отрасль.

1. Какую максимальную цену может установить картель в этой ситуации?

2. Насколько больше продукции будет продавать картель ввиду потенциальной угрозы конкурента?

3. Какой суммой прибыли готов пожертвовать картель, чтобы не допустить прихода конкурента? 243

 

№ 49. Отраслевой спрос представлен функцией: Q^D = 52 – P. В отрасли работают 6 конкурирующих фирм с одинаковыми затратами: TC_i = 9 + 10 q_i + 4 q ² _i, где q _i – объем выпуска одной фирмы; для других фирм вход в отрасль закрыт. Собственник одной из фирм уговорил четырех других отдать ему свой бизнес, обязавшись выплачивать им ренту, на 1/9 превышающую получаемую ими прибыль от производства.

1. Насколько больше прибыли после выплаты ренты будет оставаться у собственника-монополиста по сравнению с той, которую он получал в роли конкурента?

2. Какая цена установится в длинном периоде, если при неизменных издержках производства отрасль станет открытой?

3. Сколько фирм будет работать в открытой отрасли?

№ 50. В отрасли работают 10 фирм с одинаковыми функциями затрат TC_i = 4 + 2 q_i + 0,5 . Отраслевой спрос задан функцией: Q^D = 52 – 2 P. Собственник одной из фирм предложил своим конкурентам передать ему все предприятия, обещая за это выплачивать им регулярный доход, в 2 раза превышающий получаемую ими прибыль.

1. Насколько возрастет прибыль инициатора монополизации отрасли, если его предложение будет принято?

2. Насколько сократятся излишки потребителей?

 

№ 51. Спрос на продукцию отображается функцией Q^D = 140 – 4 P, а общие затраты на ее производство – функцией TC = 100 + 10 Q + Q ². Продукция продается на рынке совершенной конкуренции. Во сколько раз должны снизится переменные затраты, чтобы при переходе от совершенной конкуренции к монополии цена не изменилась?

 

№ 52. Маркетинговый отдел фирмы установил следующую зависимость числа покупателей, готовых покупать товар по разным ценам в разном количестве (в сутки):

Цена/Количество	1 кг	2 кг	3 кг	4 кг	5 кг

Товар покупается по цене 1 руб. за ед.

Определить схему ценообразования а) при единой цене, б) при нелинейном ценообразовании. Рассчитать цены и прибыль.

№ 53. Длина города равна 60 км. Магазин первого дуополиста расположен в точке А на расстоянии 6 км от левого конца города (точка М). Магазин второго – в точке В на расстоянии 8 км от правого конца города. Стоимость перевозки равно 1 ден. ед. на км. Дуополисты максимизируют выручку. Потребители проживают равномерно по всей длине города. Найти расположение точки Е, в которой проживает потребитель, затраты которого на покупку единицы товара (включающие транспортные расходы) одинаковы для обоих магазинов.

 

№ 54. Пусть функция спроса имеет вид: P = a – q₁ – q₂. Первая фирма точно знает чему равен параметр а, а вторая знает лишь, что с вероятностью 0.5 он равен 4, с вероятностью 0.3 равен 8, с вероятностью 0.2 равен 10. Фирмы выбирают между объемами продаж 2 и 6. Представить дерево решений, если фирмы взаимодействуют по Штакельбергу.

 

№ 55. Предположим, что рыночный спрос определяется функцией P = 60 – q₁ – q_{2 .} Затраты двух фирм имеют вид: TC₁ = 5 q₁, TC₂ = 4 q₂. В момент принятия решения об объеме выпуска 1-ая фирма полагает, что с вероятностью 60% затраты 2-ой фирмы TC₂ = 4 q₂, а с вероятностью 40%: TC₂ = 6 q₂. Вторая фирма считает, ч то с вероятностью 50% затраты первой фирмы TC₁ = 5 q₁, а с вероятностью 50%: TC₁ = 10 q₁. Каждый участник знает, как оценивает его затраты конкурент. Выведите уравнения реакции первой и второй фирмы исходя из асимметричности информации.

 

№ 56. Длина города равна 40 км. Магазин первого дуополиста расположен в точке А на расстоянии 6 км от левого конца города (точка М). Магазин второго – в точке В на расстоянии 2 км от правого конца города. Стоимость перевозки равно 1 ден. ед. на км. Дуополисты максимизируют выручку. Потребители проживают равномерно по всей длине города. Найти расположение точки Е, в которой проживает потребитель, затраты которого на покупку единицы товара (включающие транспортные расходы) одинаковы для обоих магазинов. Каковы должны быть цены у этих дуополистов?

 

№ 57. На концах линейного города (модель Хотеллинга) длиной 5 расположены две фирмы, имеющие функции затрат TC₁(q) = 30 q и TC₂(q) = 60 q. Для жителя, удаленного от фирмы, товар которой он покупает, на расстояние x, затраты на доставку продукта оцениваются величиной tx. Спрос на продукт абсолютно неэластичен и равен 1 на единицу длины. Определить равновесные цены товара каждой фирмы и прибыли фирм, если а) t = 10; б) t = 4; в) t = 1. Какие выводы можно сделать из сопоставления результатов?

 

№ 58. На рынке совершенной конкуренции с отраслевым спросом 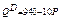торговали фирмы с одинаковыми затратами . В определенный момент 10 фирм образовали картель, став ценовым лидером. Насколько в результате этого возросла цена и сократился объем продаж?

 

№ 59. Фирма, продает стиральный порошок некоторой марки и стремится к определению оптимальной стратегии в области рекламы. В январе фирма увеличила цену на порошок с 20 до 25 руб., а объем продаж сократился с 30 до 26 тыс. пачек. В феврале фирма увеличила расходы на рекламу на 20% по сравнению с январем. Объем продаж возрос с 26 тыс. до 28 тыс. Определите оптимальную долю расходов на рекламу в выручке фирмы.

 

№ 60. Рассмотрим модель, в которой предпочтения потребителя относятся не к продуктам, а к характеристикам, которыми продукты обладают (модель Ланкастера). Допустим, что рассматривается множество продуктов, обладающих двумя характеристиками (X и Y).

Обозначим (xi, yi) количественные меры соответствующих характеристик в единице i -го продукта, причем простоты ради в качестве единицы каждого продукта принимается количество продукта, приобретаемое за одну денежную единицу. Будем считать, что предпочтения в пространстве Потребление и спрос. 17 характеристик удовлетворяют тем же аксиомам, что и предпочтения в пространстве благ в традиционной теории. В таблице (см. выше) приведены данные по шести различным продуктам. Какие из них не имеют перспектив быть проданными на рынке?

 

Поделиться:

Воспользуйтесь поиском по сайту: