Линейная производственная задача

Государственное образовательное учреждение

Высшего профессионального образования

Государственный Университет Управления

 

Кафедра прикладной математики

 

 

Курсовая работа

По дисциплине «Прикладная математика»

Выполнил
Институт	Мировой и Национальной Экономики
Специальность	Менеджмент организации
Специализация	Предпринимательство
Отделение	д/о
Курс	II
Группа
Руководитель	Курочкин А.П.
Дата сдачи на проверку
Дата защиты
Оценка
Подпись руководителя

 

Москва 2002

Оглавление
	Стр.
1. Линейная производственная задача…………………………………..	3-6
2. Двойственная задача…………………………………………………...	7-8
3. Задача о «расшивке узких мест производства»……………………...	9-10
4. Транспортная задача линейного программирования………………..	11-13
5. Динамическое программирование. Распределение капитальных вложений…………………………………………………………………...	14-16
6. Матричная игра как модель конкуренции и сотрудничества……….	17-18
7. Анализ доходности и риска финансовых операций…………………	19-20
8. Задача формирования оптимального портфеля ценных бумаг……..
Использованная литература……………………………………………...

Линейная производственная задача

Предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известны технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли.

Технологическая матрица A, в которой каждый элемент a_ij означает необходимое количество i-го ресурса для выпуска j-го вида продукции:

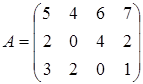
Вектор B объемов ресурсов, каждый элемент которого b_i означает предельное количество i-го ресурса для выпуска всего объема продукции:

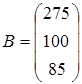
Вектор удельной прибыли C, элементы которого c_j означают прибыль от производства единицы продукции j-го вида:

Количество каждого из товаров задаётся с помощью производственной программы:

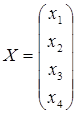, где

x1, x2, x3, x4 - кол-во 1-ой, 2-ой, 3-ей и 4-ой продукции соответственно.

Технологическая матрица затрат показывает какое количество ресурсов требуется для производства 1 единицы продукции. Каждому виду продукции соответствует столбец в технологической матрице затрат А. Каждая строка матрицы А соответствует одному из видов ресурсов. Чтобы получить расход каждого ресурса при заданной производственной программе перемножим матрицу А и вектор производственной программы X:

Каждый элемент полученного вектора равен расходу соответствующего ресурса при заданной производственной программе, т.е. при x1, x2, x3, x4. Так как матрица А указывает на необходимое количество определённого ресурса для производства 1 единицы продукции, то умножая это число на общее количество продукции данного вида мы получим расход данного ресурса для производства заданного количества определённого вида продукции. Сложив расход ресурса по всем видам продукции, мы получим общий расход ресурса.

Вектор В указывает на располагаемое количество ресурсов. Каждый элемент соответствует одному виду ресурса. Таким образом, при производстве при заданной производственной программе X и объеме располагаемых ресурсов B должны выполняться неравенства для каждого ресурса:

5x₁+ 4x₂+ 6x₃+ 7x₄#275; 2x₁+ 4x₃+ 2x₄#100; 3x₁ + 2x₂ + x₄ #85

Вектор С указывает на прибыль от продажи 1 единицы продукции каждого вида. Каждый элемент вектора соответствует одному виду продукции. Чтобы найти прибыль от каждого вида продукции следует помножить вектор производственной программу X на вектор удельной прибыли С:

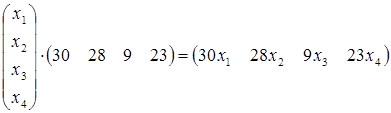
Сложив элементы полученного вектора мы получим совокупную прибыль от продажи всей продукции при заданном векторе производственной программы X. Так как x₁, x₂, x₃, x₄ – неизвестные запишем полученное выражение в виде функции:

Z = 50x₁ + 27x₂ + 34x₃ + 54x₄

Для достижения максимальной прибыли требуется найти максимум полученной функции Z. При этом x₁, x₂, x₃, x₄ по смыслу ³ 0. Учитывая условия ограничения по ресурсам, получим задачу на условный экстремум:

Z = 50x₁ + 27x₂ + 34x₃ + 54x₄Ymax

x₁$0, x₂ $0, x₃ $0, x₄ $0

Для ее решения систему неравенств при помощи дополнительных неизвестных х₅, х₆, х₇ заменим системой линейных алгебраических уравнений

Z = 50x₁ + 27x₂ + 34x₃ + 54x₄Ymax

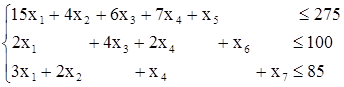
x₁$0, x₂ $0, x₃ $0, x₄ $0

 

где дополнительные переменные имеют смысл остатков соответствующих ресурсов, а именно

х₅ – остаток ресурса 1-го вида,

х₆ – остаток ресурса 2-го вида,

х₇ – остаток ресурса 3-го вида.

Решаем полученную задачу симплексным методом (методом направленного перебора базисных допустимых решений):

C	Базис	Hi	х1	х2	х3	х4	х5	х6	х7	α
	Х5									39,3
	Х6
	Х7
	Z – Z0		-50	-27	-34	-54
	X4	275/7	5/7	4/7	6/7		1/7
	Х6	150/7	4/7	-8/7	16/7		-2/7			37,5
	Х7	320/7	16/7	10/7	-6/7		-1/7
	Z – Z0	14850/7	-80/7	27/7	86/7		54/7
	Х4			1/8	9/8		3/16		-5/16
	Х6			-3/2	5/2		-1/4		-1/4
	Х1			5/8	-3/8		-1/16		7/16
	Z – Z0

Как видно из последней симплексной таблицы, оптимальная производственная программа имеет вид

х₁ = 20, х₂ = 0, х₃ = 0, х₄ = 25,

а максимальная прибыль равна

Z_max = 2350

При этом 1-й и 3-й ресурсы будут исчерпаны полностью (х₅=0, х₇=0), а 2-й ресурс будет иметь остаток х₆ = 10 единиц.

При выполнении производственной программы 2-й и 3-ий ресурсы используются полностью, то есть образуют “узкие места производства”.

Проверим получившийся результат.

Воспользуемся тем, что в оптимальной производственной программе x₂ = 0 и x₃ = 0. Предположим, что вторую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными. Математическая модель будет выглядеть следующим образом:

Z = 50x₁ + 54x₄ ®max

x₁ ³ 0, x₄ ³ 0

Графическое решение этой задачи представлено на Рис. 1.

Из графика видно, что результаты совпадают.

Обращенный базис, отвечающий оптимальной производственной программе, содержится в последней симплексной таблице:

Для того, чтобы убедиться в правильности полученного решения, следует проверить отношение Н = Q^-1 * В:

Двойственная задача

Некое предприятие, использующее те же ресурсы что и предприятие из предыдущей задачи, желает приобрести все эти ресурсы. Оно желает приобрести их по ценам y₁, y₂ и y₃ соответственно за единицу каждого из трёх ресурсов. Из условий предыдущей задачи нам известны затраты всех 3-х ресурсов для производства для каждого из 4-х видов продукции, количество ресурсов на производстве и прибыль от единицы каждой продукции:

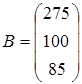
Так как продажа ресурсов должна быть целесообразной, то прибыль от продажи единице каждого вида продукции должна быть меньше, чем прибыль от продажи ресурсов в количестве равном затрате этих ресурсов для производства единицы продукции каждого вида.

Для производства продукции 1-ого вида требуется 5 единиц 1-ого ресурса, 2 единицы 2-ого ресурса и 3 единицы 3-его ресурса, что соответствует элементам 1-ого столбца матрица А. Прибыль от продажи продукции 1-ого вида равна 50. Следовательно, для целесообразности продажи ресурсов прибыль от продажи 5 единиц 1-ого ресурса, 2-х единиц 2-ого ресурса и 3-х единиц 3-его ресурса должна быть больше, либо равна 50, т.е. прибыли от продажи продукции 1-ого вида:

Соответственные условия должны выполняться и для продукции других видов. Им соответствуют 2-ой, 3-ий и 4-ый столбцы матрицы А, а также 2-ой, 3-ий и 4-ый элементы матрицы-строки прибыли С:

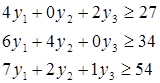
Но при продаже требуется учитывать и интересы покупателя. Естественным желанием покупателя является снижение расходов. Так как предприятие желает закупить весь объём имеющихся ресурсов, то его затраты при ценах y₁, y₂ и y₃ составят 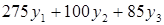, где коэффициенты при y₁, y₂ и y₃ - количество имеющихся ресурсов. Таким образом:

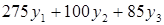Y min

 

Кроме того, так как цены не могут быть отрицательными, то .

Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений х(х₁,х₂,х₃) и у(у₁,у₂,у₃) пары двойственных задач необходимо и достаточно выполнение условий:

и

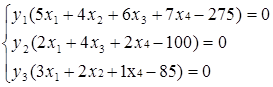
Ранее (см. Задачу 1) было найдено, что в решении исходной задачи х₁>0 и х₄>0. Поэтому

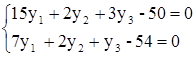
Учитывая, что 2-ой ресурс был избыточным, то, согласно теореме двойственности, его двойственная оценка 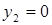, получим систему:

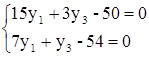
откуда следует

у₁ = 7,

у₃ = 5.

Таким образом, получили двойственные оценки ресурсов:

у₁ = 7, у₂ = 0, у₃ = 5,

причем общая оценка всех ресурсов равна

f_min = 2350

Заметим, что это решение содержалось в последней строке симплексной таблицы исходной задачи.

Данные значения y₁, y₂ и y₃ являются двойственными оценками соответствующих ресурсов, т.е. оценка единицы 1-ого ресурса равна 7, оценка единицы 2-ого ресурса равна 0, а оценка 3-его ресурса равна 5. Эти оценки являются «теневыми» ценами ресурсов. Экономически они указывают, на сколько увеличится прибыль при выполнении оптимальной производственной программы, если количество соответствующего ресурса увеличить на единицу, при неизменном количестве остальных ресурсов.

Используя задачу 1, мы можем найти оценку технологии, т.е. на сколько уменьшится прибыль, если будет произведена 1 единица продукции не по оптимальной программе. Оценки технологий получились в конечной симплексной таблице как коэффициенты при соответствующих x в целевой функции. Таким образом, при производстве единицы 2-ой продукции прибыль упадёт на 11, а для 3-ей продукции падение составит 8.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: