 |
Методология модельного исследования
|
|
|
|
В процессе компьютерного моделирования, независимо от применяемого метода, можно определить обобщенную матодологическую схему модельного исследования (рис. 5). Предложенная формализованная методологическая последовательность предусматривает несколько основных фаз, представленных ниже. В основном, она представляет итерационную процедуру для получения необходимой достоверности разрабатываемой компьютерной модели на базе формулировки начальной модельной гипотезы и ее последовательной модификации. Такой подход является удачным при исследовании сложных систем, а также и при отсуствии достаточной априорной информации для исследуемого обьекта.
Стадия "Формулирование"
На первом этапе разработки модели необходимо точно и ясно определить объект моделирования, условия и гипотезы исследования, а также критерии оценки модельной эффективности. Это позволит разработать концептуальную модель и дефинировать ее абстрактными терминами и понятиями. Обычно абстрактное описание определяет начальные принципы модельного построения (основные апроксимации, дефиниционные области переменных, критерии эффективности и типы ожидаемых результатов). На этой стадии можно определить следующие подэтапы:
Дефинирование и анализ поставленной задачи. Включает ясно определенную сущность задачи исследования и планирование необходимых мероприятий. На базе анализа проблемы определяется объем предпологаемых действий и необходимость декомпозиции задачи.
Уточнение типа начальной информации. Эта информация позволяет получить корректные выходные результаты моделирования и поэтому надо обеспечить необходимый уровень достоверности оценок.
|
|
|
Введение допусщенйх и гипотез. Это необходимо при отсуствии достаточной информации для реализации модели. Допусщения заменяют отсуствующие данные, либо отсуствие их полности. Гипотезы относятся к типу возможных результатов или к среде реализации исследуемых процессов. В процессе моделирования эти гипотезы и допусщения могут быть приняты, отброшены, либо модифицированы.
Определение основного содержания модели. На базе применяемого метода моделирования отчитывается особеность реального объекта, поставленая задача и средства ее решения. Результаты этого подэтапа включают формулировку базовой концепции модели, формализованное описание реальных процессов и выбор подходящей апроксимацией.
Определение модельных параметров и выбор критериев эффективности. На этом подэтапе определяются первычные и вторычные факторы, входные воздействия и ожидаемые на выходе реакции модели, что является особенно важным для достижения необходимой точности математического описания. Уточнение критериев эффективности связано с дефинированием функциональных зависимостей оценки реакции системы при изменении модельных параметров.
Абстрактное описание модели. Фаза общего формулирования концептуальной модели заканчивает построение абстрактой модели в подходящей среде абстрактных терминов - например, в виде структурной схемы, как потоковой диаграмы (Data Flow Diagram), в виде графической схемы (State Transition Network) и т.д. Это абстрактное представление позволить легко построить математическую модель.

Рис. 5. Методологическая схема модельного исследования.
Стадия "Проектирование"
Проектирование компьютерной модели связано с разработкой математической модели и ее программным описанием.
Математическая модель является представлением структуры исследуемого объекта и протекающих процессов в подходящем математическом виде Y=Ф(X, S, A, T), где: X - множество внешних воздействий; S - множество системных параметров; A - отражает функциональное поведение (алгоритмы функционирования); T - время работы. Таким образом поведение (реакция) объекта Y моделирует набор функциональных воздействий Ф, представляющих аналитические зависимости (детерминированные или вероятностные). В этом смысле, математическая модель является описанием абстрактной модели средствами выбранной математической системы, оценивая принятые гипотезы и апроксимации, начальные условия и дефинированные параметры исследования. При разработке математической модели возможно применить известные математические формулы, зависимости или математические законы (например, вероятностные распределения), а также комбинировать и дополнить их. Самые распространенные для цели моделирования теоретические математические системы предоставляют возможность представить математическую модель и в графическом виде - сети Петри [Music, 2003], цепи Маркова [Benveniste, 2003], системы массового обслуживания [Pockec, 2001] и др. На базе определенных на предыдущей стадии критериев, созданную математическую модель необходимо оценить с целью достижения необходимой степени достоверности и адекватности, и после этого можно утвердить или отбросить ее.
|
|
|
Программная модель представляет собой реализацию математического описания программным языком - для этого выбираются подходящие технические и технологические средства. В процессе программной реализации на базе математической модели разработывается логическая структурно-функциональная схема модели. Для построения этой схемы можно использовать традиционные блок-схемы, либо графические средства, которые представляются специализированной средой моделирования - как например в GPSS (General Purpose Simulation System) [Stahl, 2001]. Программная реализация модели является задачей разработки программного обеспечения и в этом смысле подчиняется принципам технологии программирования.
Стадия "Уточнение"
Действия этой стадии предназначенны для полной валидизации проектированной модели и утверждения ее адекватности. Существенное значение для их эффективности имеет оценка текущей адекватности на предыдущих стадиях. В этом смысле процесс уточнения модели надо рассмотривать как совокупность распределенных действий на всех предыдущих стадиях компьютерного моделирования. В общем плане, стадию уточнения можно представить как итеративную процедуру (рис. 6), позволяющую последовательную модификацию начальной версии разрабатываемой модели.
|
|
|
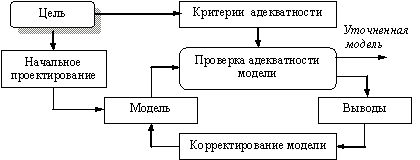
Рис. 6. Итеративная процедура для уточнения модели.
Основной целью проверки модельной достоверности является определение уровня точности соответствия при представлении процессов реального объекта и механизма регистрации модельных результатов. В общем плане, компьютерная модель представляет совокупность отдельных компонентов и в этом смысле особенно важно правильно планировать проверки адекватности.
Стадия "Выполнение"
Это этап реализации созданной модели (решение численным методом либо выполнение во времени). Самая главная цель - получение максимальной информации для минимальных затрать машинного времени. Предусмотрены два подэтапа:
Планирование модельного эксперимента - определение значения управляемых факторов и правила регистрации наблюдаемых факторов при выполнении модели. Выбор конкретного плана эксперимента зависит от поставленной цели исследования при оптимизации времени выполнения. Для получения эффективного плана обычно применяются статистические методы (полный план, однофакторный план, рандомизированный план и т.д.), позволяющие удалить совместное влияние наблюдаемых факторов и оценить допустимую экспериментальную ошыбку.
Реализация эксперимента - подготовка входных данных, компьютерная реализация экспериментального плана и сохранение экспериментальных результатов. Реализацию эксперимента можно выполнить следующим образом: контрольное моделирование (для проверки работоспособности и чувствительности модели и оценки модельного времени); рабочее моделирование (действительная реализация разработанного плана эксперимента).
Стадия "Анализ и интерпретация модельных результатов"
|
|
|
При реализации плана модельного эксперимента накапливается информация (результаты моделирования), которую необходимо анализировать для получения оценки и выводов о поведении исследуемого объекта. Это определяет два аспекта - выбор методов для анализа экспериментальной информации и применение подходящих способов интерпретации полученных оценок. Последнее особенно важно для формирования коректных выводов исследования. В смысле первого аспекта обычно применяют статистические методы - дискриптивные анализы (подсчет граничных значений параметров, математического ожидания, дисперсии и средне-квадратической ошибки; определение расслоения для выбранного фактора; вычисление гистограммы и др.); корреляционный анализ (определение уровня факторной взаимосвязи); регрессионный анализ (исследование причинной взаимосвязи в группе факторов); дисперсионный анализ (для устанавливания относительного влияния определенных факторов на базе экспериментальных результатов).
Результаты анализа модельных данных можно представить в числовом или табличном виде, при помощи графических зависимостей, диаграмм, гистограмм и пр. Чтобы выбрать подходящие графические средства существенное значение имеет использованный метод анализа, а также субъективные умения экспериментатора для оформления результатов эксперимента.
Заключение
Основная цель организации каждого модельного эксперимента - это реализация эффективного моделирования. Она связывается с машинным временем - значительный объем обработки в моделе повышает стоимость моделирования и понижает эффективность. Для эффективности исследования существенное значение имеет быстрая валидизация модели и достижение сходимости. Для каждой реальной системы часто приходится создавать множество разных моделей, отличающихся способом декомпозиции и уровнем детайлизации, методом моделирования, средствами программной реализации и т.д. В процессе выбора оптимального варианта только оценка точности и адекватности является недостаточной. Из множества сходимых моделей надо выбрать самый эффективный вариант, который тратить минимальное время на реализацию.
Существенное значение для достижения достаточной эффективности модели имеет и применяемый язык программной реализации, а также полность формальной системы абстрактного представления концептуальной модели, простота терминов описания, разработывание оптимального плана и др. Применение универсальных программных систем отличается отсуствием специфических языковых операторов и поэтому они являются подходящими прежде всего для аналитического моделирования. Для реализации симуляционных моделей удачно использовать специализированные языковые среды.
|
|
|
Список литературы
[Брююль 2002] Брююль А. SPSS: искусство обработки информации. Анализ статистических данных. Санкт Петербург: ДиаСофт, 2002, - 608 с.
[Романски, 2001] Романски Р. Математическое моделирование и исследование стохастических временных характеристик процессов компютерной обработки данных // Информационные технологии. - Москва, Россия, 2001, No 2, - С. 51 - 55.
[Arons, 2000] Arons H., van Asperen E. Computer assistance for model definition // Proceedings of the 32nd Winter Simulation Conference. - Florida, USA, December 2000. - P. 399-408.
[Benveniste, 2003] Benveniste A., Fabre E., Haar St. Markov nets: probabilistic models for distributed and concurrent systems // IEEE Transactions on Automatic Control. November 2003, vol. 48, No 11. - P. 1936-1950.
[Butler, 2001] Butler J.E., Brockman J. B. A Web-based learning tool that simulates a simple computer architecture // ACM SIGCSE Bulletin. June 2001, vol. 33, No. 2. - P. 47-50.
[Crosbie, 2000] Crosbie R. E. A model curriculum in modeling and simulation: Do we need it? Can we do it? // Proceedings of the 32nd Winter Simulation Conference. December 2000. -P. 1666-1668.
[Fabre, 2002] Fabre E., Pigourier V. Monitoring distributed systems with distributed algorithms // Proceedings of the 41st IEEE Conference on Decision and Control. - vol. 1. 10-13 December 2002 - P. 411-416.
[Ibbett, 2002] Ibbett R.N. WWW Visualisation of Computer Architecture Simulations // Procedings of the 7th Annual Conf. on Innovation and Technology in Computer Science Education. June 2002. - P. 247.
[Lilja,2001] Lilja D.J. Comparing Instructional Delivery Methods for Teaching Computer Systems Performance Analysis // IEEE Trans. on Education. February 2001, vol. 44, No 1, - P. 35-40.
[Music, 2003] Music G., Zupancic B., Matko D. Petri net based modeling and supervisory control design in Matlab // Proceedings of the IEEE Conference EUROCON 2003 "Computers as a Tool". - vol. 1. 22-24 Sept. 2003. - Slovenia. - P. 362-366.
[Pandey, 2003] Pandey S., Ramamritham K., Chakrabarti S. Monitoring the dynamic Web to respond to continuous queries // Proceedings of the 12th International Conference on World Wide Web. - Hungary, May 2003, - P. 659-668.
[Pockec, 2001] Pockec P., Mardini W. Modeling with queues: an empirical study // Proceedings of the Canadian Conference on Electrical and Computer Engineering. - vol. 1. 13-16 May 2001. - P. 685-689.
[Romansky, 2002] Romansky R. et all. An Organization of Informational Network InfoNet for Distributed e-Learning // Proceedings of the 3rd International Conference оn Computer Systems and Technologies (e-Learning). 20-21 June 2002. Sofia, Bulgaria. - P. IV.4-1 - IV.4-6.
[Sargent, 2003] Sargent R.G. Verification and validation of simulation models // Proceedings of the 2003 Winter Simulation Conference. - vol. 1. 7-10 December 2003. - P. 27-48.
[Stahl, 2001] Stahl, I. GPSS: 40 years of development // Proceedings of the 33rd Winter Simulation Conference. December 2001. - P. 577-585.
[Ye, 2002] Ye D, Xiaofer Xu, Yuliu Chen. Integrated modeling methodology for virtual enterprises // Proceedings of the 10th Conference on Computers, Communications, Control and Power Engineering. - vol. 3. October 2002. - P. 1603-1606.
|
|
|


