Методы решения частных задач.

Математические основы теории систем

Задания к курсовой работе на тему:

Математическое моделирование функционирования систем

(гр. 15ЗПА51)

 

Пенза 2017

ЦЕЛЕВАЯ УСТАНОВКА КУРСОВОЙ РАБОТЫ

 

Целью выполнения курсовой работы является закрепление знаний, полученных студентом в процессе самостоятельного изучения дисциплины.

В результате выполнения курсовой работы должен появиться навык и умение практического использования полученных знаний для решения некоторых теоретических и практических задач.

ЗАДАНИЯ

Передаточная функция системы имеет вид:

. (1)

Значения коэффициентов a_i и b_j для различных вариантов приведены в табл. 1.1.

Таблица 1.1

Значения коэффициентов a_i и b_j

№ вар-та				z

 

Методы решения частных задач.

Таблица 1.2

Методы решения частных задач

№ вар-та	Метод решения СЛАУ	Метод интегрирования	Метод решения нелинейного уравнения
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления
	Метод Гаусса	Метод Симпсона	Метод Ньютона
	Метод Гаусса	Метод трапеций	Метод секущих
	Метод Гаусса	Метод Симпсона	Метод простых итераций
	Метод Гаусса	Метод трапеций	Метод половинного деления

Порядок выполнения работы:

1. Записать дифференциальное уравнение системы. Найти характеристическое уравнение и его корни. Нахождение корней реализовать в Matlab заданным методом, оформив метод в виде отдельной функции.

2. Разложить передаточную функцию на сумму простых слагаемых. Нахождение коэффициентов реализовать в Matlab заданным методом, оформив метод в виде отдельной функции. Вычислить импульсную переходную характеристику w (t) с помощью обратного преобразования Лапласа и переходную характеристику h (t). Вычисление интеграла h (t) реализовать в Matlab заданным методом, оформив метод в виде отдельной функции.

3. В пакете Matlab построить характеристики w (t) и h (t).

4. Построить логарифмические амплитудно-частотную (ЛАЧХ) и фазочастотную (ЛФЧХ) характеристики в Matlab.

5. Записать уравнения состояния в нормальной форме, изобразить схему моделирования.

6. Записать уравнения состояния в канонической форме, изобразить схему моделирования.

7. Решить уравнения состояния в нормальной и канонической формах. Характеристические числа матрицы Фробениуса найти с использованием стандартных функций Matlab. Получить аналитическое выражение для переходного процесса y (t), если на входе действует сигнал u (t) = a ₂·l(t), а начальные условия имеют вид y (0) = 0,1 a ₂; .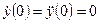

8. Проверить, одинаково ли значение коэффициента усиления по передаточной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики.

9. При составлении программы в Matlab не использовать SIMULINK. Программа должна представлять собой отдельный файл Matlab с расширением *.m.

Методические указания.

Передаточная функция системы W (s) – это отношение изображения по Лапласу сигнала на выходе к изображению по Лапласу сигнала на входе при нулевых начальных условиях.

Чтобы перейти от передаточной функции к дифференциальному уравнению системы, нужно перейти из области изображений по Лапласу во временную область. Из (1) следует

;

.

Для перехода во временную область воспользуемся формальными правилами:

.

Тогда дифференциальное уравнение системы имеет вид:

. (2)

Характеристическое уравнение системы определяется знаменателем передаточной функции:

.

Корни данного многочлена (нелинейного уравнения) , , можно определить следующими методами:

- методом половинного деления;

- методом Ньютона;

- методом секущих;

- методом простых итераций.

Далее передаточная функция системы записывается в форме нулей и полюсов. Затем разлагаем передаточную функцию на сумму простых слагаемых, используем метод неопределенных коэффициентов.

Полученную СЛАУ решаем одним из следующих методов:

- методом Гаусса;

- методом простых итераций.

В итоге записываем передаточную функцию с учетом найденных коэффициентов.

Импульсная переходная характеристика w (t) – это процесс изменения сигнала на выходе при подаче на вход δ - функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.

В соответствии с таблицами соответствия 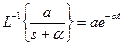. Проведем преобразование .

Переходная характеристика h (t) – это процесс изменения сигнала на выходе системы при подаче на вход единичного ступенчатого воздействия. Преобразование по Лапласу l(t) это , следовательно, .

Переходную характеристику можно также вычислить следующим образом:

.

Данный интеграл вычисляется одним из следующих методов:

- методом трапеций;

- методом Симпсона.

Построение асимптотических ЛАХ и ФЧХ.При определении частотных характеристик подразумевается, что на входе и выходе системы сигналы являются гармоническими.

Амплитудно-частотная характеристика (АЧХ) показывает, как изменяется отношение выходного сигнала к входному в зависимости от частоты. Фазочастотная характеристика (ФЧХ) показывает изменение сдвига фаз между входным и выходным сигналами в зависимости от частоты.

ЛАЧХ строится в двойных логарифмических шкалах. По одной логарифмической оси откладывается круговая частота w, по другой значение L (w) = 20lg K, выраженное в децибелах. Асимптотическая ЛАЧХ состоит из отрезков прямых линий с наклонами кратными 20 дБ/дек.

Кроме входных и выходных переменных при описании систем выделяют переменные x, связанные с внутренней структурой устройства, – переменные состояния. Тогда систему можно описать с помощью уравнений состояния.

Нормальная форма уравнений состояния имеет вид:

. (3)

Здесь А – квадратная матрица определенного вида, размер которой определяется порядком дифференциального уравнения. Элементы, стоящие над главной диагональю – единицы, элементы нижней строки – коэффициенты левой части дифференциального уравнения, взятые с противоположным знаком. Все остальные элементы – нули. Такая матрица называется матрицей Фробениуса:

.

Элементы матриц B и D вычисляются по рекуррентным соотношениям.

Подставив в (3) рассчитанные матрицы, получим систему дифференциальных уравнений 1-го порядка.

На основе полученной системы строим схему модели, например:

Запишем уравнения состояния в канонической форме. Для этого введем новую переменную состояния q, которая связана с переменной состояния x следующим образом: х = М q. М – это модальная матрица, которая имеет вид:

,

где - характеристические числа матрицы Фробениуса.

При подстановке q вместо x в нормальную форму уравнений состояния (3) получим уравнения состояния системы в канонической форме:

Здесь:

;

;

;

.

Подставив найденные значения матриц в (4), получим систему дифференциальных уравнений 1-го порядка относительно q.

На основе полученной системы строим схему модели, например:

Найдем решение y (t) для системы уравнений в нормальной форме, если заданы начальные условия.

Решение уравнения состояния складывается из двух составляющих x (t) = x ₁(t) + x ₂ (t) – свободной и вынужденной.

Свободная составляющая x₁ (t) – это общее решение дифференциального уравнения системы с нулевой правой частью. Оно не зависит от внешнего воздействия и характеризует естественное поведение системы.

Вынужденная составляющая x ₂(t) – это частное решение дифференциального уравнения с ненулевой правой частью. Оно зависит от сигнала u (t) и характеризует поведение системы под его воздействием.

Решение уравнения состояния имеет вид:

,

где - фундаментальная матрица или матрица перехода.

Она вычисляется по следующей формуле:

,

где - неизвестные коэффициенты.

Вычислить их можно, решая матричное уравнение:

.

Найдем решение уравнений состояния, представленных в канонической форме (4). Каждое из дифференциальных уравнений первого порядка зависит только от одной переменной, и его решение в общем виде имеет вид:

.

Проверяем решение нормальных и канонических уравнений.

Проверим, одинаково ли значение коэффициента усиления: по передаточной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики.

После проверки делаем соответствующие выводы.

ПОРЯДОК ОФОРМЛЕНИЯ РАБОТЫ

 

Курсовая работа должна иметь титульный лист, содержание, условия задач, решение задач, выводы, список использованной литературы. Курсовая работа представляется в формате Word 2003 (шрифт Times New Roman, 13 пт., межстрочный интервал – 1,5) с необходимым количеством иллюстраций (графики, диаграммы, таблицы). Оформление в соответствии с Положением о курсовом проектировании ПГУ.

ЛИТЕРАТУРА

 

1. Кузнецов, В. П. Теория автоматического управления: конспект лекций. В 2 ч. ч. 1 / В. П. Кузнецов, С. В. Лукьянец, М. А. Крупская. – Минск: БГУИР, 2007.

2. Ушаков, А. В. Математические основы теории систем: Элементы теории и практикум: учеб. пособие / А. В. Ушаков, В. В. Хабалов, Н. А. Дударенко. – СПб: СПб ГУ ИТМО, 2007.

3. Певзнер, Л. Д. Математические основы теории систем / Л. Д. Певзнер, Е. П. Чураков. – М.: Высш. шк., 2009.

4. Ерофеев, А. А. Теория автоматического управления: учеб. для вузов /А. А. Ерофеев. – СПб.: Политехника, 2003.

5. Пакет компьютерных программ Matlab 2012…2016.

Поделиться:

Воспользуйтесь поиском по сайту: