 |
Вспомогательные функции в MS Excel
|
|
|
|
Вычисление коэффициентов регрессии осуществляется с помощью функции ЛИНЕЙН()
ЛИНЕЙН (Значения_y; Значения_x; Конст; статистика)
Значения_y — массив значений y.
Значения_x — необязательный массив значений x, если массив х опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как и Значения_y.
Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если аргумент Конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения a подбираются так, чтобы выполнялось соотношение y=ax.
Статистика — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициент a и постоянную b.
Для вычисления множества точек на линии регрессии используется функция ТЕНДЕНЦИЯ
ТЕНДЕНЦИЯ (Значения_y; Значения_x;Новые_значения_x; Конст)
Значения_y — массив значений y, которые уже известны для соотношения y = ax + b.
Значения_x — массив значений x.
Новые_значения_x — новый массив значений, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Если Новые_значения_x опущены, то предполагается, что они совпадают с массивом значений х.
Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если Конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения a подбираются таким образом, чтобы выполнялось соотношение y=ax.
|
|
|
Необходимо помнить, что результатом функций ЛИНЕЙН, ТЕНДЕНЦИЯ является множество значений – массив.
Для расчета коэффициента корреляции используется функция КОРРЕЛ, возвращающая значения коэффициента корреляции
КОРРЕЛ (Массив1; Массив2)
Массив1 — массив значений x. Массив2 — массив значений y. Массив1 и Массив2 должны иметь одинаковое количество точек данных.
РЕАЛИЗАЦИЯ В EXCEL
К пунктам 1–2 задания 2. Определение вида зависимости между полученными данными с использованием встроенных функций Microsoft Excel.
Рассмотрим построение линии регрессии с помощью MS Excel на примере следующей задачи. Известна табличная зависимость G(L). Построить линию регрессии и вычислить ожидаемое значение в точках 0, 0.75, 1.75, 2.8,4.5.
Введем таблицу значений в лист MS Excel и построим точечный график. Рабочий лист примет вид (см. рис. 2).
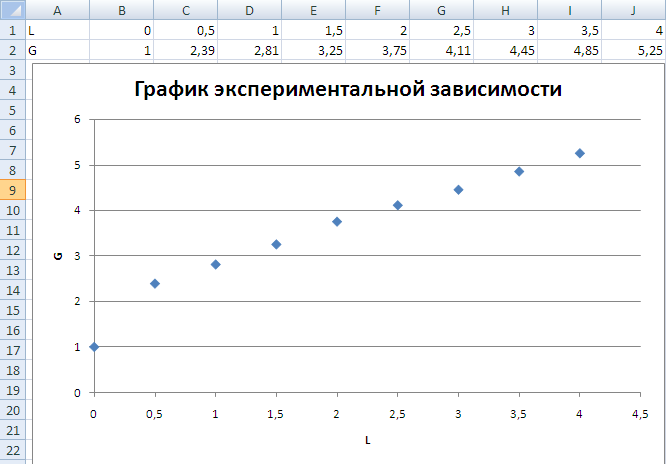
Рисунок 2
Чтобы в ячейках K2, L2 получить коэффициенты линейной зависимости a и b необходимо выделить эти две ячейки мышью, выбрать функцию ЛИНЕЙН в списке статистических функций
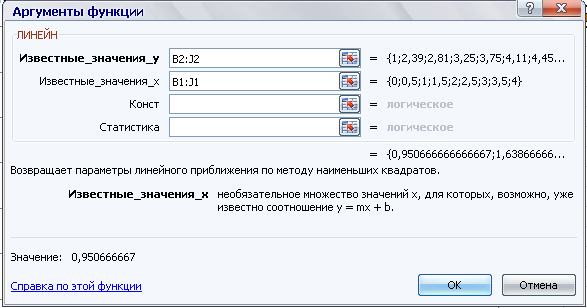
Ввести в поле Известные_значения_y значения из ячеек B2:J2, а в поле Известные_значения_x значения из ячеек B1:J1. Нажать Ok. Не забыть, что функция ЛИНЕЙН работает со значениями x и y в виде массивов. Т. е. необходимо нажать F2, а затем Ctrl+Shift+Enter. В результате получим следующие коэффициенты (см. рис 3)
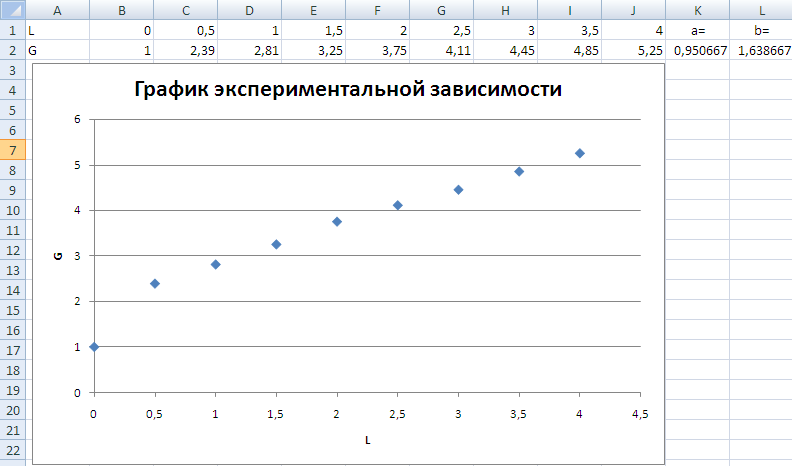
Рисунок 3
В ячейке M2 будет рассчитываться значение коэффициента корреляции, для чего туда следует ввести формулу =КОРРЕЛ(B1:J1;B2:J2). В результате рабочий лист примет вид (см. рис. 4).
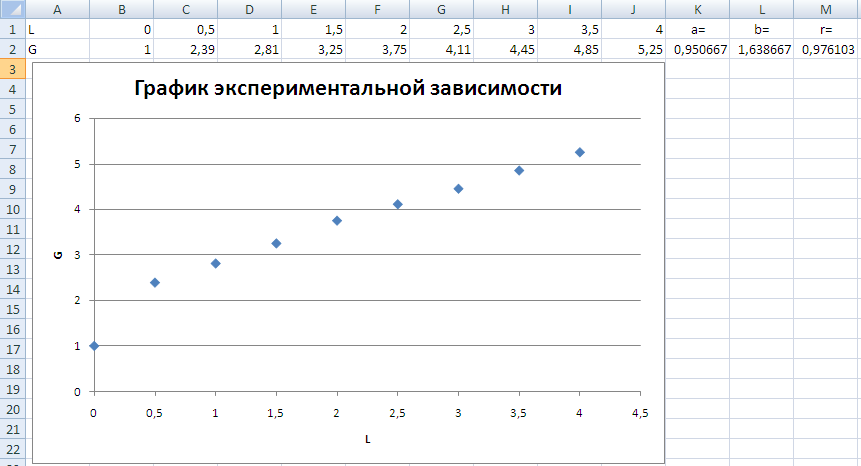
Рисунок 4
Теперь с помощью функции ТЕНДЕНЦИЯ вычислим ожидаемое значение в точках 0, 0.75, 1.75, 2.8, 4.5. Для этого в ячейки L9:L13 занесем эти значения, а в ячейки M9:M13 введем формулу =ТЕНДЕНЦИЯ(B2:J2;B1:J1;L9:L13) для расчета ожидаемых значений. Для этого выделим ячейки M9:M13 выберем в списке статистических функций функцию ТЕНДЕНЦИЯ и заполним ее как указано ниже:
|
|
|
Нажимаем OK. Так как функция ТЕНДЕНЦИЯ работает с данными как с массивами то необходимо дополнительно нажать F2, а затем Ctrl+Shift+Enter.
В результате получим следующие значения.
| x | y |
| 1,638667 | |
| 0,75 | 2,351667 |
| 1,75 | 3,302333 |
| 2,8 | 4,300533 |
| 4,5 | 5,916667 |
Изобразим линию регрессии на диаграмме. Для этого выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и выберем команду Исходные данные. В появившемся диалоговом окне (см. рис. 5), для добавления линии регрессии щелкнем по кнопке Добавить.
Рисунок 5
В качестве имени введем Линия регрессии, в качестве Значения Х L9:L13, в качестве Значения Y M9:M13. Далее выделяем линию регрессии, для изменения ее типа щелкаем правой кнопкой мыши и выбираем команду Тип диаграммы ( рис. 6 ). Для форматирования линии регрессии дважды щелкаем по ней (рис. 7), можно изменить толщину линии, цвет, тип маркера и т.д.
Рисунок 6 Рисунок 7
После форматирования графика рабочий лист примет вид, изображенный на рис. 8.
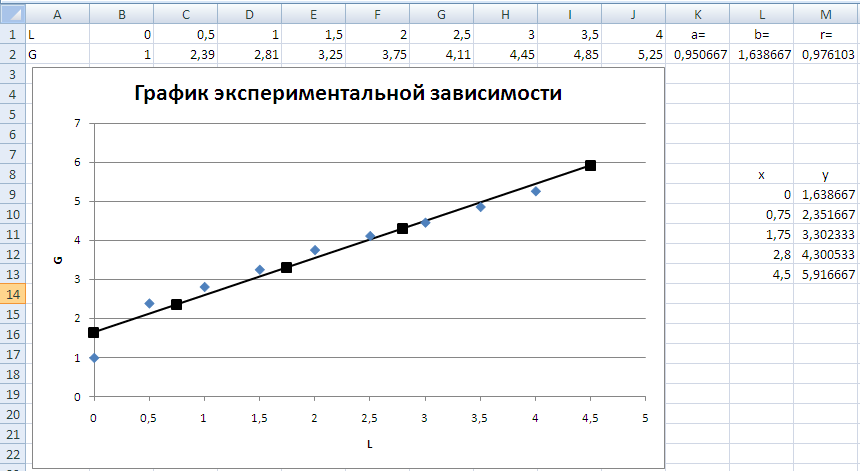
Рисунок 8
Квадратичная функция
Необходимо определить параметры функции y=a0+a1*x+a2*x2.
Составим функцию
Для этой функции запишем систему уравнений:
Получим
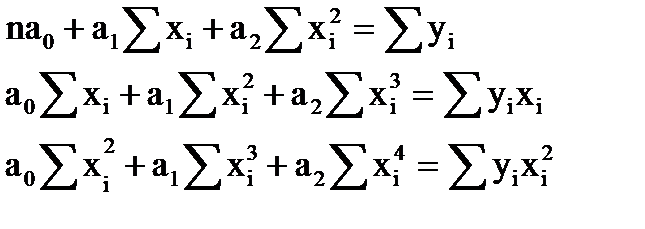
Для нахождения параметров a0, a1, a2 необходимо решить эту систему линейных алгебраических уравнений (например, методом Крамера или методом обратной матрицы).
Кубическая функция
Необходимо определить параметры многочлена третьей степени: y=a0+a1*x+a2*x2+a3*x3.
Составим функцию S:
Система уравнений для нахождения параметров a0, a1, a2, a3 имеет вид:
Для нахождения параметров a0, a1, a2, a3 необходимо решить систему четырёх линейных алгебраических уравнений.
Если в качестве аналитической зависимости выберем многочлен k-й степени y=a0+a1x+...+ak xk, то система уравнений для определения параметров ai принимает вид:
К пункту 3 задания 2. Нахождение коэффициентов зависимости с помощью блока «Поиск решения»
Пусть в результате эксперимента получена следующая зависимость Z(T)
Необходимо подобрать коэффициенты зависимости Z(t)=At4+Bt3+Ct2+Dt+K методом наименьших квадратов.
Эта задача эквивалентна задаче нахождения минимума функции пяти переменных
|
|
|
Введем табличную зависимость в рабочий лист MS Excel и построим график функции (см. рис. 9).
Рисунок 9
Рассмотрим процесс решения задачи оптимизации. Пусть значения А, В, С, D и К хранятся в ячейках K1:K5. Для этого в ячейки K1:K5 введем произвольные числа. Теперь в 23-ю строку введем значения функции 
. В ячейку B23 введем значение функции в первой точке (ячейка B1) =$K$1*B1^4+$K$2*B1^3+$K$3*B1^2+$K$4*B1+$K$5. Получим ожидаемое значение в точке B1. Затем растянем эту формулу на весь диапазон B23:J23. В 24-ю строку введем квадраты разности между экспериментальными и расчетными точками. В ячейку B24 введем формулу =(B23-B2)^2 и растянем эту формулу на весь диапазон B24:J24. В ячейку В25 будем хранить суммарную квадратичную ошибку. Для этого введем формулу =СУММ(B24:J24).
Теперь осталось с помощью решающего блока (Сервис \ Поиск решения) (при его отсутствии нужно установить его Сервис / Надстройки / в окне Надстройки установите флажок Поиск решения / ОК) решить задачу оптимизации без ограничений. Этот блок установит минимум в ячейки B25 (формула 
) изменяя содержимое ячеек K1:K5 (переменные А, В, С, D и К) (см. рис. 10).
Рисунок 10
После этого в ячейках K1:K5 получим значения параметров функции А, В, С, D и К функции . В ячейках B23:J23 получим ожидаемые значение функции в исходных точках. Поместим эти точки в виде отдельной линии на графике. В ячейке B25 будет храниться суммарная квадратичная ошибка. В результате рабочий лист примет вид (см. рис. 11).
Рисунок 11
Ø На рабочих листах должны быть графики экспериментальной и рассчитанных теоретических зависимостей.
Примечание:
Для включения надстройки «Поиск решения» в меню Файл выберите пункт ПАРАМЕТРЫ, перейдите на вкладку НАДСТРОЙКИ, выделите пункт ПОИСК РЕШЕНИЯ и нажмите на кнопку «Перейти». Кнопка «Поиск решения» появится на ленте «Данные» (см. рисунки 12 и 13).
Рисунок 12
Рисунок 13
|
|
|
