Учебно-методические материалы по дисциплине

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

«Кузбасский государственный технический университет

Имени Т. Ф. Горбачева»

филиал КузГТУ в г. Новокузнецке

 

МОДЕЛИРОВАНИЕ ТРАНСПОРТНЫХ ПРОЦЕССОВ

Задания контрольной работы для студентов группы АТбз-41

 

Автор-составитель:

к.ф.-м.н., Маркидонов А.В.

 

Новокузнецк, 2017

 

УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАБОТЫ

Вариант заданий является индивидуальным, и выбирается по номеру студента в зачетной ведомости или списку группы. Все задания представлены в общем виде. Значения неизвестных параметров необходимо выбрать из соответствующей таблицы, указанной в приложении. Контрольная работа выполняется в табличном редакторе MS Excel.

 

 

Задание 1.

Даны векторы допустимых альтернатив Х = { x_i } (i = 1,.., 4) и состояний среды Y = { y _j} (j = 1,.., 5). Решив задачу принятия решений в условиях неопределенности определить оптимум функции полезности W (X, Y) (см. табл.1) по критерию Лапласа, Вальда, Гурвица и Сэвиджа.

Таблица 1

	y 1	y 2	y 3	y 4	y 5
x 1	W 11	W 12	W 13	W 14	W 15
x 2	W 21	W 22	W 23	W 24	W 25
x 3	W 31	W 32	W 33	W 34	W 35
x 4	W 41	W 42	W 43	W 44	W 45

 

 

Задание 2.

Рассчитать верхнюю и нижнюю цены для матричной антагонистической игры двух компаний, заданной платежной матрицей P, где выигрышем считается доля рынка в %. Используя геометрический метод (если это возможно) найти решение в смешанных стратегиях и определить цену игры.

 

 

 

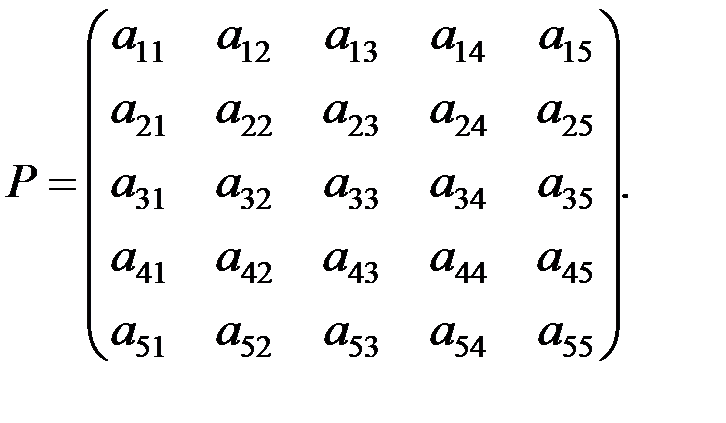
Задание 3.

Магазин может завезти в различных пропорциях товары четырех типов (А ₁, A ₂, А ₃, А ₄), их реализации и прибыль магазина зависят от вида товара и состояния спроса. Предполагается, что спрос может иметь три состояния (В ₁, В ₂, В ₃)и не прогнозируется. Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантирован­ной прибыли при следующей матрице прибыли (см. табл. 2)

 

Таблица 2

Тип товара	Спрос
В 1	В 2	В 3
А 1	а 11	а 12	а 13
А 2	а 21	а 22	а 23
А 3	а 31	а 32	а 33
А 4	а 41	а 42	а 43

 

Задание 4.

Устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное случайное время. Возможные состояния системы: S₀ – оба узла исправны; S₁ – первый узел ремонтируется, второй исправен; S₂ – второй узел ремонтируется, первый исправен; S₃ - оба узла ремонтируются. Граф системы приведен на рисунке. Найти предельные вероятности для системы S.

 

 

Найти средний чистый доход от эксплуатации в стационарном режиме системы S если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден. ед., а их ремонт требует затрат соответственно в 4 и 2 ден. ед.

 

 

Задание 5.

В автохозяйстве n автомобилей. Каждый из них в среднем ломается в год m раз, и ремонт длится в среднем 1 месяц. Определить, какую долю времени все автомобили исправны и среднее число исправных автомобилей в произвольный момент времени.

 

 

Задание 6.

Мыловаренный завод выпускает моющие средства, используя для всех них одно и то же оборудование. Очистка оборудования и подготовка его к производству данного вида моющих средств обходится в A тыс. ден. ед. Интенсивность спроса на данное моющее средство составляет B т в месяц. Издержки производства на тонну продукции составляют C ден. ед. Стоимость хранения одной тонны моющего средства в месяц равна D ден. ед. Чему равен оптимальный объем продукции, производимой за один цикл, если дефицит не допускается? Чему равна продолжительность цикла? Чему равны общие затраты?

 

 

Задание 7.

Потребность сборочного предприятия в деталях некоторого типа составляет A тыс. деталей в год, причем эти детали расходуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объема, указанного в заказе. Хранение детали на складе стоит B ден. ед. в сутки, а поставка партии – C тыс. ден. ед. Задержка производства из-за отсутствия деталей недопустима. Определить наиболее экономичный объем партии и интервал между поставками, которые нужно указать в заказе (предполагается, что поставщик не допускает задержки поставок). Определить, на сколько процентов увеличатся затраты на создание и хранение запаса по сравнению с минимальными затратами при объеме заказываемых партий D тыс. деталей. Предположим, что заказываются не все партии сразу, а каждая отдельно, причем срок выполнения заказа равен E дней. Определить точки заказа, т. е. при каком уровне запаса следует заказывать следующую партию. Найти наиболее экономичный объем партии и интервал между поставками, сохраняя все условия, кроме недопустимости дефицита, если известно, что отсутствие на сборке каждой детали приносит в сутки убытки в размере F ден. ед.

 

ПРИЛОЖЕНИЕ

 

Таблица 1

Значения неизвестных параметров для задания 1

Параметр	В1	В2	В3	В4	В5	В6	В7	В8	В9	В10
w 11
w 12
w 13
w 14
w 15
w 21
w 22
w 23
w 24
w 25
w 31
w 32
w 33
w 34
w 35
w 41
w 42
w 43
w 44
w 45
Параметр	В11	В12	В13	В14	В15	В16	В17	В18	В19	В20
w 11
w 12
w 13
w 14
w 15
w 21
w 22
w 23
w 24
w 25
w 31
w 32
Таблица 1 (продолжение)
w 33
w 34
w 35
w 41
w 42
w 43
w 44
w 45
Параметр	В21	В22	В23	В24	В25	В26	В27	В28	В29	В30
w 11
w 12
w 13
w 14
w 15
w 21
w 22
w 23
w 24
w 25
w 31
w 32
w 33
w 34
w 35
w 41
w 42
w 43
w 44
w 45
Параметр	В31	В32	В33	В34	В35	В36	В37	В38	В39	В40
w 11
w 12
w 13
w 14
w 15
w 21
w 22
Таблица 1 (продолжение)
w 23
w 24
w 25
w 31
w 32
w 33
w 34
w 35
w 41
w 42
w 43
w 44
w 45

 

 

Таблица 2

Значения неизвестных параметров для задания 2

Параметр	В1	В2	В3	В4	В5	В6	В7	В8	В9	В10
а 11
а 12
а 13
а 14
а 15
а 21
а 22
а 23
а 24
а 25
а 31	–2
а 32
а 33
а 34
а 35
а 41
а 42
а 43
а 44
Таблица 2 (продолжение)
а 45
а 51
а 52
а 53	–1
а 54
а 55	–1
Параметр	В11	В12	В13	В14	В15	В16	В17	В18	В19	В20
а 11
а 12
а 13
а 14
а 15
а 21
а 22
а 23		–4
а 24		–4
а 25
а 31
а 32
а 33						–2
а 34
а 35
а 41
а 42
а 43
а 44
а 45
а 51
а 52
а 53
а 54
а 55
Параметр	В21	В22	В23	В24	В25	В26	В27	В28	В29	В30
а 11
а 12
а 13
а 14
Таблица 2 (продолжение)
а 15
а 21
а 22
а 23
а 24
а 25
а 31
а 32
а 33
а 34
а 35
а 41
а 42
а 43
а 44
а 45
а 51
а 52
а 53
а 54
а 55
Параметр	В31	В32	В33	В34	В35	В36	В37	В38	В39	В40
а 11
а 12
а 13
а 14
а 15
а 21
а 22
а 23
а 24
а 25
а 31
а 32										–1
а 33
а 34
а 35
Таблица 2 (продолжение)
а 41
а 42
а 43
а 44
а 45
а 51
а 52									–1
а 53
а 54
а 55									–2

 

 

Таблица 3

Значения неизвестных параметров для задания 3

Параметр	В1	В2	В3	В4	В5	В6	В7	В8	В9	В10
а 11
а 12
а 13
а 21
а 22
а 23
а 31
а 32
а 33
а 41
а 42
а 43
Параметр	В11	В12	В13	В14	В15	В16	В17	В18	В19	В20
а 11
а 12
а 13
а 21
а 22
а 23
а 31
а 32
а 33
Таблица 3 (продолжение)
а 41
а 42
а 43
Параметр	В21	В22	В23	В24	В25	В26	В27	В28	В29	В30
а 11
а 12
а 13
а 21
а 22
а 23
а 31
а 32
а 33
а 41
а 42
а 43
Параметр	В31	В32	В33	В34	В35	В36	В37	В38	В39	В40
а 11

Поделиться:

Воспользуйтесь поиском по сайту: