Объем информации V (объемный подход).

Лекция № 3

Меры информации. 1

Объем информации V (объемный подход). 3

Количество информации / (энтропийный/вероятностный подход). 4

Контрольные вопросы.. 7

Меры информации

При реализации информационных процессов всегда происхо­дит перенос информации в пространстве и времени от источника информации к приемнику. При этом для передачи информации используют различные знаки или симво­лы, например естественного или искусственного (формального) языка, позволяющие выразить ее в форме сообщения.

Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 40-х годов XX века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.

С точки зрения семиотики (от греч. semeion — знак, признак) — науки, занимающейся исследованием свойств знаков и знаковых систем сообщение, может изучаться на трех уровнях:

• синтаксическом, где рассматриваются внутренние свойства сообщений, т. е. отношения между знаками, отражающие структуру данной знаковой системы.

Синтаксическая мера количества информации оперирует обезличенной информацией, не выражающей смыслового отношения к объекту. Объем данных в сообщении измеряется количеством символов (разрядов) в этом сообщении.

 

• семантическом, где анализируются отношения между знаками и обозначаемыми ими предметами, действиями, качествами, т. е. смысловое содержание сообщения, его отношение к источнику информации;

Для измерения смыслового содержания информации, т.е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Для этого используется понятие тезауруса пользователя.

Тезаурус – это совокупность сведений, которыми располагает пользователь или система.

В зависимости от соотношений между смысловым содержанием информации и тезаурусом пользователя изменяется количество семантической информации, воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус. Максимальное количество семантической информации потребитель приобретает при согласовании ее смыслового содержания со своим тезаурусом, когда поступающая информация понятна пользователю и несет ему ранее неизвестные (отсутствующие в его тезаурусе) сведения. Следовательно, количество семантической информации в сообщении, т.е. количество новых знаний, получаемых пользователем, является величиной относительной. Одно и то же сообщение может иметь смысловое содержание для компетентного пользователя и быть бессмысленным (семантический шум) для пользователя некомпетентного.

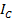Относительной мерой количества семантической информации может служить коэффициент содержательности , который определяется как отношение количества семантической информации к ее объему :

 

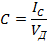
• прагматическом, где рассматриваются отношения между сообщением и получателем, т. е. потребительское содержание сообщения, его отношение к получателю.

Таким образом, проблемы передачи информации тоже разделяют на три уровня: синтаксический, семантический и прагматический.

Проблемы синтаксического уровня - это чисто технические проблемы совершенствования методов пере­дачи сообщений и их материальных носителей — сигналов. На этом уровне рассматривают проблемы доставки получателю сообщений как совокупности знаков, учитывая при этом тип носителя и спо­соб представления информации, скорость передачи и обработки, размеры кодов представления информации, надежность и точность преобразования этих кодов и т. п. При этом полностью абстрагируются от смыслового содержания сообщений и их целевого предназначе­ния. На этом уровне информацию, рассматриваемую только с син­таксических позиций, обычно называют данными, так как смыс­ловая сторона при этом не имеет значения.

Проблемы семантического уровня связаны с формализацией и учетом смысла передаваемой информации. На данном уров­не анализируются те сведения, которые отражает информация, выявляется смысл, содержание информации, осуществ­ляется ее обобщение.

Проблемы этого уровня чрезвычайно сложны, так как смысло­вое содержание информации больше зависит от получателя, чем от семантики сообщения, представленного на каком-либо языке.

На прагматическом уровне интересуют последствия от полу­чения и использования данной информации потребителем. Про­блемы этого уровня связаны с определением ценности и полезно­сти информации для потребителя Основная сложность здесь со­стоит в том, что ценность, полезность информации может быть совершенно различной для различных получателей и, кроме того, она зависит от ряда факторов, таких, например, как своевременность ее доставки и использования.

Современная теория информации исследует в основном про­блемы синтаксического уровня. Она опирается на понятие «количе­ство информации», которое никак не отражает ни смысла, ни важности переда­ваемых сообщений. В связи с этим иногда говорят, что теория ин­формации находится на синтаксическом уровне.

Для каждого из рассмотренных выше уровней проблем переда­чи информации существуют свои подходы к измерению количе­ства информации и свои меры информации. Различают соответ­ственно меры информации синтаксического уровня, семантичес­кого уровня и прагматического уровня. Однако в силу вышесказанного остановимся лишь на мерах информации синтаксического уровня.

Итак, количественная оценка информации этого уровня не связана с содержательной стороной информации, а оперирует с обезличен­ной информацией, не выражающей смыслового отношения к объекту. В связи с этим данная мера дает возможность оценки ин­формационных потоков в таких разных по своей природе объек­тах, как системы связи, вычислительные машины, системы управ­ления, нервная система живого организма и т. п.

Для измерения информации на синтаксическом уровне вводят­ся два параметра: объем информации (данных) — V (объемный подход) и количество информации — / (вероятностный подход).

Объем информации V (объемный подход).

При реализации ин­формационных процессов информация передается в виде сообще­ния, представляющего собой совокупность символов какого-либо алфавита. При этом каждый новый символ в сообщении увеличи­вает количество информации, представленной последовательнос­тью символов данного алфавита. Если теперь количество инфор­мации, содержащейся в сообщении из одного символа, принять за единицу, то объем информации (данных) V в любом другом сооб­щении будет равен количеству символов (разрядов) в этом сооб­щении. Так как одна и та же информация может быть представле­на многими разными способами (с использованием разных алфавитов), то и единица измерения информации (данных) соответ­ственно будет меняться.

В компьютерной технике наименьшей единицей измерения информации является 1 бит. Таким образом, объем информации, записанной двоичными знаками (0 и 1) в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. Напри­мер, восьмиразрядный двоичный код 11001011 имеет объем дан­ных V= 8 бит.

В современной вычислительной технике наряду с минимальной единицей измерения данных «бит» широко используется укруп­ненная единица измерения «байт», равная 8 бит. При работе с боль­шими объемами информации для подсчета ее количества приме­няют более крупные единицы измерения, такие как килобайт (Кбайт), мегабайт (Мбайт), гигабайт (Гбайт), терабайт (Тбайт):

1 Кбайт = 1024 байт = 2¹⁰ байт;

1 Мбайт = 1024 Кбайт = 2²⁰ байт = 1 048 576 байт;

1 Гбайт = 1024 Мбайт = 2³⁰ байт = 1 073 741 824 байт;

1 Тбайт = 1024 Гбайт = 2⁴⁰ байт = 1 099 511 627 776 байт.

Следует обратить внимание, что в системе измерения двоичной (компьютерной) информации, в отличие от метрической системы, единицы с приставками «кило», «мега» и т. д. получаются путем умножения основной единицы не на 10³= 1000, 10⁶= 1000 000 и т. д., а на 2¹⁰ , 2²⁰ и т. д.

Количество информации / (энтропийный/вероятностный подход)

Часто приходится иметь дело с явлениями, исход которых неоднозначен и зависит от факторов, которые мы не знаем или не можем учесть. Например – определение пола будущего ребенка, результат бросания игральной кости и пр.

Определение: события, о которых нельзя сказать произойдут они или нет, пока не будет осуществлен эксперимент, называются случайными.

Раздел математики, в котором строится понятийный и математический аппарат для описания случайных событий, называется теорией вероятности.

Определение: осуществление некоторого комплекса условий называется опытом, а интересующий нас исход этого опыта – благоприятным событием. Тогда, если N – общее число опытов, а N_A-количество благоприятных исходов случайного события А, то отношение N/N_A, называется относительной частотой появления события А. Однако, очевидно, в разных сериях, значение частоты может оказаться различным. Действительно, например, в серии из трех опытов по бросанию монеты может 2 раза выпасть орел и 1 раз решетка. Если благоприятным событием считать выпадение орла, то частота получается равно 2/3. Очевидно, что в другой серии она может быть равно 0 или 1 или 1/3. Однако, оказывается, что при увеличении количества опытов значение относительной частоты все меньше и меньше отклоняется от некоторой константы. Скачки могут быть, но все реже и реже. Наличие этой константы называется статистической устойчивостью частот, а сама константа вероятностью случайного события А. В случае, если все исходы опыта конечны и равновозможны, то их вероятность равна P=1/n, где n-число возможных исходов.

Пример:

1. вероятность выпадения орла при бросании монеты – ½.

2. вероятность вытянуть из урны красный шар (при условии, что там три шара – красный, синий, белый) – 1/3.

Таким образом, когда мы имеем дело со случайными событиями, имеется некоторая неопределенность. Введем в рассмотрение численную величину, измеряющую неопределенность опыта.

Определение: Энтропия – мера неопределенности опыта, в котором проявляются случайные события. Обозначим ее H.

Очевидно, что величины H и n (число возможных исходов опыта) связаны функциональной зависимостью: H=f(n), то есть мера неопределенности есть функция числа исходов.

Некоторые свойства этой функции:

1. f(1)=0, так как при n=1 исход не является случайным и неопределенность отсутствует.

2. f(n) возрастает с ростом n, так как чем больше возможных исходов, тем труднее предсказать результат, и, следовательно, больше неопределенность.

3. если и два независимых опыта с количеством равновероятных исходов 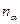и , то мера их суммарной неопределенности равна сумме мер неопределенности каждого из опытов:

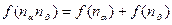
Всем трем этим свойствам удовлетворяет единственная функция – log(n). То есть за меру неопределенности опыта с n равновероятными исходами можно принять число log(n). Вопрос – по какому основанию? В силу известной формулы 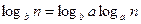выбор основания значения не имеет, следовательно можно взять в качестве основания логарифма 2. Таким образом:

H= - это формула Хартли. (5)

 

Преобразовывая, получим: 2^H=n

 

Все nисходов рассмотренного выше опыта являются равновероятными и поэтому можно считать, что на «долю» каждого исхода приходится одна 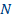-я часть общей неопределенности опыта: 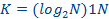. При этом вероятность i -го исхода 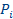равняется, очевидно, . Таким образом,

 

- формула Шеннона. (6)

 

Замечание: в случае, если исходы опыта не равновероятны, справедлива формула Шеннона: , где p_i-вероятность i-того исхода.

Какова же связь энтропии с информацией?

Из определения энтропии следует, что энтропия это числовая характеристика, отражающая ту степень неопределенности, которая исчезает после проведения опыта, то есть ПОСЛЕ ПОЛУЧЕНИЯ ИНФОРМАЦИИ. То есть, после проведения опыта получаем определенную информацию. Следовательно:

Энтропия опыта равна той информации, которую мы получаем в результате его осуществления. То есть:

Определение: информация I – это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом; убыль связанной с ним энтропии является количественной мерой информации.

Значит, если H1 – начальная энтропия (до проведения опыта), H2 – энтропия после проведения опыта, то информация

I=H1-H2=log₂n₁-log₂n₂=log₂(n₁/n₂).

Очевидно, что в случае, когда получен конкретный результат, H2=0, и, таким образом, количество полученной информации совпадает с начальной энтропией и подсчитывается при помощи формулы Хартли.

Итак, мы ввели меру неопределенности – энтропию и показали, что начальная энтропия (или убыль энтропии) равна количеству полученной в результате опыта информации. Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, значение H будет равно 1 при n=2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (например, бросание монеты). Такая единица количества информации называется "бит".

Замечание: вероятностный подход учитывает ценность информации для конкретного получателя (действительно, веlь речь идет о благоприятных (ля кого-то!!) событиях).

Пример: определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака "пробел". По формуле Хартли: H=log₂34=5 бит (здесь считаем, что появление каждой буквы равновероятно). По формуле Шеннона (для неравновероятных исходов) это значение равно 4,72 бит. Здесь значение, полученное по формуле Хартли – максимальное количество информации, которое моет приходиться на один знак.

 

 

Контрольные вопросы

1. Вероятностный и объемный поход к измерению количества информации.

2. Понятие энтропии.

3. Элементы теории вероятностей (определения: случайное событие, вероятность, опыт, исход)

Поделиться:

Воспользуйтесь поиском по сайту: