Представление функций алгебры логики

Логические основы построения цифровых автоматов

Основу любого дискретного вычислительного устройства со­ставляют элементарные логические схемы. Работа этих схем ос­нована на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания.

 

Основные законы и постулаты алгебры логики

 

Высказывание — некоторое предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Аппарат алгебры логики (булевой алгебры) создан в 1854 г. Дж. Булем как попытка изучения логики мышления математическими методами. Впервые практическое применение булевой алгебры было сделано К. Шенноном в 1938 г. для анализа и разработки релейных переключательных сетей, результатом чего явилась разработка ме­тода представления любой сети, состоящей из совокупности пере­ключателей и реле, математическими выражениями и принципов их преобразования на основе правил булевой алгебры. Ввиду наличия аналогий между релейными и современными электронными схема­ми аппарат булевой алгебры нашел широкое применение для их структурно-функционального описания, анализа и проектирования. Использование булевой алгебры позволяет не только более удобно оперировать с булевыми выражениями (описывающими те или иные электронные узлы), чем со схемами или логическими диаграммами, но и на формальном уровне путем эквивалентных преобразований и базовых теорем упрощать их, давая возможность создавать эконо­мически и технически более совершенные электронные устройства любого назначения. Операции булевой алгебры часто встречаются и в программном обеспечении вычислительных устройств, где они ис­пользуются для замены аппаратной логики на программную.

Аппарат булевой алгебры, как и любая другая формальная ма­тематическая система состоит из трех множеств: элементов, опе­раций над ними и аксиом.

Элементы. Схемы вычислительных устройств можно условно разделить на три группы: исполнительные, информационные и управляющие. Первые производят обработку информации, пред­ставленной в бинарной форме; вторые служат для передачи би­нарной формы информации; третьи выполняют управляющие функции, генерируя соответствующие сигналы. Во всех случаях в тех или иных точках логических схем сигналы двух различных уровней могут представляться бинарными символами {0,1} или логическими значениями {Истина (True), Ложь (False)}. Поэтому множество элементов булевой алгебры выбирается бинарным В = {0,1}, а сама алгебра называется бинарной, или переключатель­ной. Ее элементы называются константами, или логическими 0 и 1, которым в ряде случаев соответствуют бинарные цифры, в дру­гих случаях — логические значения, соответственно ложь (False) и истина (True). В дальнейшем для обозначения булевых перемен­ных будем использовать буквы латинского алфавита — х, у, z.... Набор переменных х, у, z...может рассматриваться как n-разрядный двоичный код, разрядами которого являются эти переменные.

Операции. Основными, или базовыми, операциями булевой алгебры служат (табл. 1):

И (AND), ИЛИ (OR) и НЕ (NOT).

Опера­ция И называется логическим умножением или конъюнкцией и обозначается знаком умножения {x, ∧}.

Операция ИЛИ называет­ся логическим сложением или дизъюнкцией и обозначается знаком сложения { +, v}.

Операция НЕ называется логическим отрицани­ем или инверсией (дополнением) и обозначается знаком {', ￢}.

Таблица 4.1

Базовые логические операции

Операция	Название операции	Обозначение операции
И (AND)	Логическое умножение — конъюнкция	* (умнож), ∧
ИЛИ (OR)	Логическое сложение — дизъюнкция	+, v
НЕ (NOT)	Логическое отрицание — инверсия	￢,', черта сверху элемента

 

При выполнении операций применяются отношение эквивален­тности «=» и скобки «()», которые определяют порядок выполнения операций. Если скобок нет, то операции выполняются в сле­дующей последовательности: логическое отрицание, логическое умножение и логическое сложение.

 

ОСНОВНЫЕ ЗАКОНЫ И ПОСТУЛАТЫ АЛГЕБРЫ ЛОГИКИ

Аксиомы (постулаты) алгебры логики

1. Дизъюнкция двух переменных равна 1, если хотя бы одна из них равна 1:

0 + 0 = 0;

0+1 = 1;

1+0=1;

1 + 1 = 1.

1. Конъюнкция двух переменных равна 0, если хотя бы одна переменная равна 0:

0x0 = 0;

0x1 = 0;

1x0 = 0;

1x1 = 1.

Инверсия одного значения переменной совпадает с ее дру­гим значением:

￢1 = 0;

￢0 = 1.

Законы алгебры логики

1. Законы однопарных элементов:

a) универсального множества:

х + 1 = 1;

х * 1 = х.

b) нулевого множества:

х + 0 = x;

х * 0 = 0.

1. Законы отрицания:

a) двойного отрицания:

￢￢x=x

b) дополнительности:

x + ￢x=1

х *￢x = 0.

 

c) двойственности (де Моргана):

￢(x₁ + x₂)= ￢x₁ *￢ x₂

￢(x₁ * x₂)= ￢x₁ + ￢ x₂

1. Комбинационные законы:

a) тавтологии:

х + x = x;

х * x = х.

b) коммутативные:

x₁ + x₂=x₂ + x₁

x₁ * x₂=x₂ * x₁ (можно записывать как умножение - x₁ x₂=x₂ x₁)

c) ассоциативные (сочетательные):

x₁ + (x₂ + x₃)=(x₁ + x₂) + x₃

x₁ * (x₂ * x₃)=(x₁ * x₂) * x₃

d) дистрибутивные (распределительные):

x₁ * (x₂ + x₃)=x₁ *x₂ + x₁ *x₃

x₁ +x₂ * x₃=(x₁ + x₂) *(x₁ + x₃)

e) закон абсорбции (поглощения):

x₁ + x₁*x₂=x₁

x₁ *(x₁ + x₂)=x₁

f) склеивания:

x₁ *x₂ + x₁*￢x₂= x₁

(x₁+ x₂)*(x₁ +￢x₂) = x₁

 

Законы двойственности де Моргана были обобщены Шенноном на произвольное количество двоичных переменных: инвертиро­вание произвольной комбинации двоичных переменных, связан­ных знаками дизъюнкции и конъюнкции, эквивалентно инверти­рованию комбинаций переменных с одновременной заменой конъ­юнкции на дизъюнкцию, и наоборот:

￢(x₁ + x₂+ x₃+…+ x_n)= ￢x₁ *￢ x₂*￢ x₃*…*￢ x_n

￢(x₁ * x₂* x₃*…* x_n)= ￢x₁ +￢ x₂+￢ x₃+…+￢ x_n

 

 

Рассмотрим на примерах некоторые приемы и способы, при­меняемые при упрощении логических формул:

 

законы алгебры логики применяются в следующей последователь­ности:

правило де Моргана (заменяем первую сумму с отрицанием, получаем

сочетательный закон (убираем скобки) и коммутативный (переставляем множители, получаем

закон допол­нительности, получаем

закон тавтологии, получаем

и закон нулевого множества. Получаем в результате 0.

 

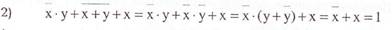
(применяется правило де Моргана, выносится за скобки общий множитель, используется закон дополнительности);

 

(выносятся за скобки общие множители; применяется закон уни­версального множества);

 

ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Булевой (переключательной, двоичной) функцией называется двоичная переменная у, значение которой зависит от значений дру­гих двоичных переменных (x₁, x₂, … x_n), именуемых аргументами:

у = (x₁, x₂, … x_n)

Задание булевой функции означает, что каждому из возмож­ных сочетаний аргументов поставлено в соответствие определен­ное значение у.

При n аргументах общее число сочетаний (возможных входных наборов аргумнтов) N = 2ⁿ. Так как каж­дому сочетанию аргументов соответствует два значения функции (О, 1), то общее число функций F = .

Булевая функция может быть задана на словах, таблично, ал­гебраически или числовым способом.

В табл. 2 представлена функция одной переменной у = у(х). При n = 1 существует 4 функции, каждая из которых имеет свое название. 120

Таблица 2. Табличное задание функции одной переменной

 

X
У0			y0=0 константа 0
У1			y1=x повторитель
У2			y2=￢x инвертор
У3			y3=1 константа 1

 

Для алгебры логики установлено, что если у = у (z1,z2) где z1 и z2— двоичные функции, т. е. z1 = z1(x1,x2), z2 = z2(x3,x4), то у = у(х1,x2,x3,x4).

Операцию замены одной функции другими функциями назы­вают суперпозицией. Эта операция дает возможность с помощью функций от малого числа аргументов получить функции большего числа аргументов. Так, при помощи суперпозиции можно получить фун­кцию с требуемым числом аргументов, используя только функцию двух аргументов.

Теперь рассмотрим функцию двух аргументов.

По определению существует 16 функций двух аргументов (табл. 3).

Таблица 3. Табличное задание функции двух переменных.

функции	Значение функции на наборах логических переменных	Наименование функции	Обозначение функции
X1
X2
f0(X1,X2)					Константа "ноль"	f(X1,X2)=0
f1(X1,X2)					Конъюнкция, произведение	f(X1,X2)= X1& X2 f(X1,X2)= X1 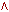X2 f(X1,X2)= X1 · X2 f(X1,X2)= X1 X2
f2(X1,X2)					Запрет по X2	X1 Δ X2
f3(X1,X2)					Переменная X1	f(X1,X2)= X1
f4(X1,X2)					Запрет по X1	X2 Δ X1
f5(X1,X2)					Переменная X2	f(X1,X2)= X2
f6(X1,X2)					Сложение по mod2 (неравнозначность)	f(X1,X2)= X1 X2
f7(X1,X2)					Дизъюнкция	f(X1,X2)= X1 X2 f(X1, X2)= X1+ X2
f8(X1,X2)					Стрелка Пирса	f(X1, X2)= X1 X2
f9(X1,X2)					Равнозначность	f(X1, X2)= X1 X2 f(X1, X2)= X1~X2
f10(X1,X2)					Инверсия X2	f(X1, X2)=^X2 f(X1, X2)=X2
f11(X1,X2)					Импликация от X2 к X1	f(X1, X2)= X2 X1
f12(X1,X2)					Инверсия X1	f(X1, X2)=^X1 f(X1, X2) = X1
f13(X1,X2)					Импликация от X1 к X2	f(X1, X2)= X1 X2
f14(X1,X2)					Штрих Шеффера	f(X1, X2)= X1|X2
f15(X1,X2)					Константа "единица"	f(X1, X2)=1

 

 

При помощи набора булевых функций двух аргументов можно описать любую цифровую систему.

На практике используют не все функции, а лишь те из них, ко­торые методом суперпозиции обеспечивают представление любой другой функции. Набор таких функций называют функционально полным набором (ФПН).

Существует несколько ФПН. В качестве ФПН применяются дизъюнкция, конъюнкция и инверсия. Этот набор называют ос­новным ФПН (ОФПН).

Кроме ОФПН, широкое применение получили:

ü функционально-полная система, включающая в себя только одну функцию — функцию Пирса (ИЛИ-НЕ);

ü функционально-полная система, включающая в себя только одну функцию — функцию Шеффера (И-НЕ).

При помощи этих функций можно построить любую цифровую систему.

Синтез логических устройств в базисе ОФПН состоит из пред­ставления этих функций в нормальных формах и минимизации.

Примеры:

Пример 1. Упростить: А ^В V А ^ В

По закону дистрибутивности вынесем А за скобки:

А ^В V А ^ В = A ^ (B V B) = А ^ 1= А

Пример 2. (первый способ)

Упростить: (А V В) ^ (А V В)

Раскроем скобки по закону дистрибутивности:

(А V В) ^ (А V В) = A V (B ^ B) =A V 0 = А

 

Пример 2. (второй способ)

Упростить: (А V В) ^ (А V В)

Перемножим скобки (как в обычной алгебре) на основании того же закона дистрибутивности:

(А V В) ^ (А V В) =

=A ^ A V A ^ B V B ^ A V B ^ B =

= A V A ^ (B V B) V 0 = = A V A ^ 1 = А

 

Пример 3.

Упростить: X V X ^ Y

На первый взгляд, пример не позволяет его упростить, так как в этом выражении ничего нельзя вынести за скобки. Заметим, что “хочется”, чтобы у переменной Х “появился” Y. Для этого представим

Х как Х ^1, а 1 распишем по закону исключенного третьего

как (Y V Y).

Далее раскроем скобки.

 

X ^(Y VY) V X ^ Y =

=X ^ Y V X ^ Y V X ^ Y =

добавим к полученному выражению X ^ Y.

Получим:

 

=X ^ Y V X ^ Y V X ^ Y V X ^ Y =

=X ^ (Y V Y) V Y ^ (X V X) =

=X ^ 1 V Y ^ 1 =

=X V Y

 

Пример 4.

Упростить: A ^ C V B ^ C V A ^ B

Один из возможных вариантов упрощения состоит в том, чтобы добавить к последнему слагаемому переменную С. Это делается стандартным способом: умножить А ^ B на 1, а 1 расписать как (С V C).

A ^ C V B ^ C V A ^ B ^ 1=

A ^ C V B ^ C V A ^ B ^ (C V C) =

A ^ C V B ^ C V A ^ B ^ C V B ^ C) =

A ^ C V B ^ C V A ^ B ^ C V A ^ B ^ C =

A ^ C ^ (1 V B) V B ^ C ^ (1 V A) =

A ^ C ^ 1 V B ^ C ^ 1 =

A ^ C V B ^ C

Пример 5.

Упростить: (X V Y)

(X V Y) =

применим закон де Моргана

X ^ Y = X ^ Y= X ^ Y

 

Поделиться:

Воспользуйтесь поиском по сайту: