Логический синтез переключательных и вычислительных схем

Логические основы построения цифровых автоматов (продолжение)

 

При помощи основных законов и постулатов алгебры логики доказывается еще ряд равносильностей. Например:

1.

2.

® - импликация (от х1 к х2 равна 0 только если х1=1, а х2=0 – из истины не выводится ложь) – «если, то»

«- логическая равнозначность (равна 1, когда оба одинаковы) – «тогда и только тогда, когда»

ПРИМЕРЫ

1. Построить таблицу истинности для высказывания

X	Y	XvY

 

2. Используя основные равносильности алгебры логики, а также равносильности и , упростить формулу .

Решение:

 

3. Для заданного высказывания :

1. построить таблицу истинности
2. упростить высказывание, используя равносильные преобразования
3. полученный результат проверить, построив для него таблицу истинности

Решение:

 

a. Таблица истинности

Обозначим

 

X	Y	Z		YZ			U

 

b. Выполним равносильные преобразования, используя и . Имеем:

(использовали правило поглощения (A&B) vAºA, далее другое правило поглощения )

 

 

c. Построим таблицу истинности для полученного выражения, тем самым проверив эквивалентность исходной и упрощенной формул

 

X	Y	Z

Продолжение.

Нормальной формой считают представление рассмотренных функций алгебры логики посредством суперпозиции вспомогательных функций – элементарной конъюнкции (конституэнты 1) или элементарной дизъюнкции (конституэнты 0). В первом случае представление булевых функций называется совершенной дизъюнктивной нормальной формой, во втором – совершенной коньюнктивной нормальной формой.

 

Элементарной конъюнкцией n переменных или конституентой единицы называется выражение, представляющее собой конъюнкцию всех переменных, причем каждая переменная может входить либо в прямом, либо в инверсном виде.

То есть например, для функции двух аргументов имеем следующие элементарные конъюнкции:

 

Элементарной дизъюнкцией n переменных или конституентой нуля называется выражение, представляющее собой дизъюнкцию всех переменных, причем каждая переменная может входить либо в прямом, либо в инверсном виде.

То есть, например, для функции двух аргументов имеем следующие элементарные дизъюнкции:

 

Форму представления булевых функций посредством суперпозиции их элементарных коньюнкций называют совершенной дизъюнктивной нормальной формой, а посредством элементарных дизъюнкций – коньюнктивной нормальной формой.

 

Любую функцию можно представить в виде совершенной дизъюнктивной или совершенной коньюнктивной нормальной форме.

Пример:

Построить СДНФ и СКНФ для функции, заданной таблицей:

Таблица 2.6 x1 x2 x3 φ(x1, x2, x3) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0

Для построения СДНФ выпишем все наборы, на которых функция равна 1: 000, 010, 101, 110. Для каждого набора построим элементарную конъюнкцию, равную единице на этом наборе:

Соединяя эти конъюнкции знаками дизъюнкции, получаем СДНФ заданной функции:

Для построения СКНФ выписываем все наборы, на которых функция равна нулю: 001, 011, 100, 111. Для каждого набора построим элементарную дизъюнкцию, равную нулю на этом наборе:

Объединяя с помощью конъюнкции все элементарные дизъюнкции, получаем КСНФ заданной функции:

Отметим, что совершенные нормальные формы не являются самым простым способом задания булевых функций. Как правило, они допускают преобразование с помощью правил булевой алгебры к более простому виду.

 

ЛОГИЧЕСКИЙ СИНТЕЗ ПЕРЕКЛЮЧАТЕЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ СХЕМ

В вычислительных и других автоматических устройствах широко применяются электрические схемы, содержащие множество переключательных элементов: реле, выключателей и т.п.. При разработке таких схем может быть использован аппарат алгебры логики.

В самом деле, проведем эксперимент.

Чтобы начать эксперимент, соедините лампочку с батарей­кой, как обычно, но включите в цепь два переключателя, а не один.

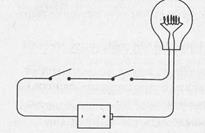
Переключатели, соединенные таким способом (один за дру­гим), называются подключенными последовательно (in series). Если вы замкнете левый переключатель, не случится ничего.

Ничего не случится, если вы замкнете правый переключатель при разомкнутом левом. Лампочка загорится лишь при одном условии: если вы включите левый и правый переключатели одновременно.

Ключевое слово тут — и. Чтобы по цепи шел ток, должны быть включены левый и правый переключатели. Эта цепь решает простую логическую задачу. Говоря по­просту, лампочка отвечает на вопрос «Оба ли переключателя замкнуты?». Работу цепи можно суммировать в небольшой таблице.

 

 

У переключателя две позиции, поэтому для его описания достаточно одного бита. Можно сказать, например, что 0 соответствует разомк­нутой цепи, а 1 — замкнутой. У лампочки также два состоя­ния, поэтому и ее можно описать одним битом. Значение 0-гого бита означает, что лампа не горит, а 1 соответствует го­рящей лампе. Теперь перепишем таблицу.

 

Заметьте: эта таблица выглядит точно также, как для оператора И (коньюнкция). То есть эта простая схема выполняет операцию И булевой алгебры.

Очевидно, что следующая схема решает задачу «Включен ли хоть один переключатель?»:

 

 

То есть два переключателя, подключенные параллельно выполняют логическую операцию ИЛИ.

Пример 1: дана фраза: «Мне нужен кот, стерилизованный, белый или рыжий; или кошка, стерилизован­ная, любого цвета, кроме белого; или любая кошка черного ок­раса». Построить устройство, определяющее подходит вам та или иная данная кошка, или нет.

Переведем это высказывание в выражение:

(MxCx(Б+P))+(ЖxCx(￢Б))+Ч

Поскольку коньюнкция – это последовательно подключенные переключатели, а дизъюнкция – параллельно, то получим следующую схему устройства:

 

 

Лампочка загорится, если кошка подходит! J

 

Итак, аппарат алгебры логики может быть успешно применен при рассмотрении переключательных и вычислительных схем. При этом, как правило, одну из основных задач: синтез или анализ схемы.

 

ПРИМЕР 2. Построение переключательной схемы

 

 

ПРИМЕР 3. Построение вычислительной схемы.

Основные этапы синтеза вычислительных схем:

1. Образование СДНФ (СКНФ) функции по заданной таблице истинности. ТИ – это табличное представление вычислительной (логической) схемы, в котором перечислены все возможные сочетания значений истинности входных сигналов вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

2. Упрощение этой функции

3. Построение соответствующей схемы.

В качестве примера логического синтеза вычислительных схем рассмотрим построение одноразрядного двоичного сумматора, имеющего два входа (х1 и x2) и два выхода (S и Р) рис. 4.4.

 

 

 

Логическая схема сумматора, реализующего данные функции, представлена на рис. 4.5.

 

 

Для логических схем И, ИЛИ, НЕ существуют типовые тех­нические схемы (логические элементы), реализующие их на по­лупроводниковых структурах.

Логический элемент — часть электронной логической схемы, ко­торая реализует элементарную логическую функцию.

К основным логическим элементам современных вычислитель­ных устройств относятся электронные схемы, реализующие опе­рации И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие.

Входные и выходные сигналы, соответствующие двум логичес­ким состояниям в логических элементах 1 и 0 — имеют один из двух установленных уровней напряжения. Например, +5 В и О В.

Высокий уровень обычно соответствует значению «истина» («1»), а низкий — значению «ложь» («О»).

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию.

Работу логических элементов описывают с помощью таблиц истинности.

Схема И. Эта схема реализует конъюнкцию двух или более ло­гических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

Связь между выходом z этой схемы и входами х и у описыва­ется соотношением: z = х х у (читается как х и у). Операция конъ­юнкции на структурных схемах обозначается знаком & (читается как амперсэнд), являющимся сокращенной записью английского слова and.

Схема ИЛИ. Эта схема реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.

Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. ниже. Знак 1 на схеме соответ­ствует обозначению, т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1. Связь между выходом z этой схемы и входами х и у описывается соотношени­ем: z =xvy (читается как х или у).

 

Схема НЕ. Схема НЕ (инвертор) реализует операцию отрица­ния. Связь между входом х этой схемы и выходом z можно запи­сать соотношением z = х, х, где х читается как «не х» или «инвер­сия X».

Если на входе схемы 0, то на выходе 1. Когда на входе 1, на вы­ходе 0. Условное обозначение инвертора представлено на следующем рис.

 

Схема И—НЕ. Схема состоит из элемента И и инвертора и осу­ществляет отрицание результата схемы И. Связь между выходом z и входами х и у схемы записывают следующим образом: z = ￢(XxY), читается как «инверсия х и у». Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представ­лено на рисунке.

 

Схема ИЛИ—НЕ. Схема состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами х и у схемы записывают следующим обра­зом: читается как «инверсия х и у». Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рисунке:

 

Тогда структурная схема рассмотренного выше сумматора в соответсвующих условных обозначениях будет выглядеть следующим образом:

 

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. На их основе строятся такие комбинационные элементы и узлы вычислительных машин как сумматоры, шифраторы, дешифраторы, адресные коммутаторы, триггеры различных типов, регистры и др.

 

Примеры:

1. Для заданной комбинационной схемы построить аналитическое выражение и, если возможно, равносильную ей упрощенную схему. Задана схема:

 

 

Здесь .

 

 

Преобразуем последнее выражение по закону Де Моргана. Получаем:

Используя законы ассоциативности и правила приоритета логических операций, получаем

Затем воспользуемся правилом поглощения , в результате получим упрощенную формулу, равносильную данной

Ей соответствует упрощенная комбинационная схема

 

 

1. Для заданной логической таблицы функции y(a,b,c) записать аналитическое выражение и построить комбинационную схему.

 

a	b	c	Y

Рассмотрим строки таблицы, в которых функция принимает значение 1. На базе этих строк построим элементарные конъюнкции по следующему правилу – единицу заменим именем аргумента, а нуль – именем аргумента с отрицанием. Полученные таким образом элементарные конъюнкции соединим знаками дизъюнкции. Для рассматриваемого примера имеем:

Объединим первое и четвертое слагаемые и вынесем за скобки bc, получаем . Объединим первое и второе слагаемые, вынесем за скобки с, а к выражению в скобках применим правило поглощения .

Получим:

Найденному аналитическому выражению соответствует схема

 

 

Поделиться:

Воспользуйтесь поиском по сайту: