 |
Умножение матрицы на матрицу («строка на столбец»)
|
|
|
|
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Матрицы
1.1. Матрицы и основные понятия, связанные с ними
Матрицей, размером 
называется прямоугольная таблица чисел вида, состоящая из 
строк и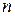 
столбцов.
Матрицы обозначаются большими буквами латинского алфавита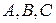 
, …
.
Матрица размера (читается «эм на эн») содержит 
чисел, называемых элементами данной матрицы.
При этом aij – это элемент матрицы, стоящий на пересечении i -й строки и j -го столбца.
i -я строка матрицы обозначается 
то есть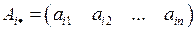 
j -ый столбец матрицы обозначается 
то есть 
Таким образом, матрицу A можно коротко записать 3-мя способами:
1. 
, i =1, 2, …, m; j =1, 2, …, n (как набор элементов);
2. 
(как столбец строк высоты );
3. 
(как строка столбцов длины ).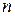
Например: 
– одна из матриц 
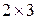, где
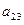=2,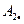 
= 
, 
.
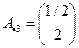Множество матриц размера обозначается 
.
Матрица называется конечной, если она состоит из конечного числа строк и столбцов, и бесконечной – в противном случае.
Матрица называется действительной, если её элементами являются действительные числа.
Виды основных матриц:
1) нулевая матрица – матрица произвольного размера, состоящая из нулей:
.
2) матрица-строка – матрица, состоящая из одной строки:
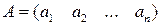
3) матрица –столбец – матрица, состоящая из одного столбца:
4) квадратная матрица – матрица, состоящая из одинакового количества строк и столбцов:
.
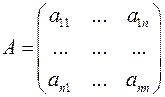В этом случае вместо «матрица размера 
» говорят «матрица порядка ».
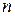Говорят, что элемент 
квадратной матрицы 
лежит на главной диагонали, если 
(номер строки равен номеру столбца). Схематично изображают так: 
.
Говорят, что элемент квадратной матрицы лежит на побочной диагонали, если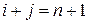 
. Схематично изображают так: 
.
5) Диагональная матрица – квадратная матрица, у которой все элементы, вне главной диагонали, равны нулю.
|
|
|
6) Единичная матрица – диагональная матрица, на главной диагонали которой стоят единицы.
Например,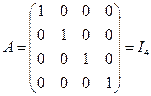 
– единичная матрица размера 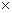4 
4.
7) Верхнетреугольная матрица – матрица у которой все элементы под главной диагональю равны 0, то есть 
, если 
.
8) Нижнетреугольная матрица (самостоятельно)
Первый слева ненулевой элемент строки называется ее разрешающим элементом.
Замечание. Нулевая строка не имеет разрешающих элементов.
9) Ступенчатая матрица – матрица у которой для любой пары соседних строк (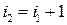
, 
) номера столбцов разрешающих элементов 
и 
удовлетворяют условию 
.
Замечание. Верхнетреугольная матрица является ступенчатой.
10) Симметрическая матрица – квадратная матрица, все элементы которой удовлетворяют условию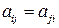 
.
Операции над матрицами
Матрицы А и В одного размера называются равными, если они совпадают поэлементно:
, i =1, 2, …, m; j =1, 2, …, n.
Сложение матриц (только одинаковых размеров)
Суммой матриц и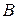 
(одинакового размера) называется матрица 
, элементы которой равны сумме элементов матриц и 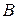, стоящих на соответствующих местах: 
, (
, 
).
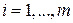Пример.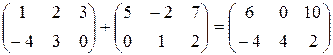 
.
Свойства:
1. Коммутативность (от перестановки слагаемых – сумма не меняется)
.
2. Ассоциативность
.
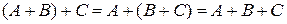3. Существование нейтрального элемента (нулевой матрицы).
Для всякой матрицы существует нулевая матрица, такая что
.
4. Существование противоположного элемента
Для всякой матрицы существует матрица, обозначаемая 
(полученная из матрицы изменением знаков всех элементов на противоположные 
), такая что
.
Доказательство всех свойств очевидным образом вытекает из соответствующих свойств для чисел.
Умножение матрицы на число
Произведением числа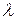 
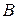на матрицу называется матрица , все элементы которой равны произведению 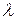на элементы матрицы , то есть
|
|
|
(, ).
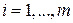Пример.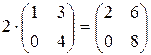 
.
Свойства.
1. Для любой матрицы : 
.
2. 
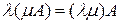– однородность.
3. Для любых чисел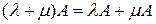 
– дистрибутивность умножения суммы чисел на матрицу.
4. 
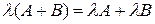– дистрибутивность умножения суммы матриц на число.
Умножение матрицы на матрицу («строка на столбец»)
Умножение А × В определено, когда число столбцов матрицы А (первого множителя) равно числу строк матрицы В (второго множителя), то есть
.
Такие матрицы А и В называются согласованными.
Произведением согласованных матриц А и В называется матрица С каждый элемент cij которой равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В:
.
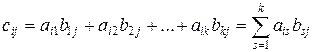Кратко правило умножения матриц называется «строка на столбец».
Например,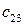 
– это сумма произведений элементов второй строки матрицы на соответствующие элементы третьего столбца матрицы :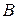
.
Пример 1. Найти произведение матриц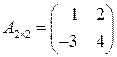 
, 
.
.
Произведение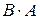 
не существует.
Пример 2. Найти произведение матриц 
, 
.
.
Матрицы и 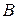– ненулевые, а их произведение является нулевой матрицей.
|
|
|
