 |
IV. Основные формулы стереометрии.
|
|
|
|
Теоремы и общие сведения
X. Стереометрия без формул.
I. Прямые и плоскости.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.
1. Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.
2. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Признак параллельности прямой и плоскости:
3. Если прямая, принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Две плоскости называются параллельными, если они не пересекаются.
Признак параллельности плоскостей:
4. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Признак перпендикулярности прямой и плоскости:
5. Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна данной плоскости.
Теорема о трех перпендикулярах:
6. Для того, чтобы прямая лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной.
II. Многогранники.
Призма. Призмой называется многогранник, у которого две грани (основания призмы) – равные многоугольники с соответственно параллельными сторонами, а все остальные грани – параллелограммы, плоскости которых параллельны одной прямой.
|
|
|
Призма, боковые ребра которой перпендикулярны основаниям, называется прямой призмой. Прямая призма называется правильной, если ее основания – правильные многоугольники.
Параллелепипед и куб. Параллелепипедом называется призма, у которой основаниями служат параллелограммы.
Прямым параллелепипедом называется параллелепипед, боковые ребра которого перпендикулярны основаниям.
Прямоугольным параллелепипедом называется прямой параллелепипед, основания которого прямоугольники.
Кубом называется прямоугольный параллелепипед с равными ребрами.
Пирамидой называется многогранник, у которого одна грань, называемая основанием, представляет собой многоугольник, а все остальные грани – треугольники, имеющие общую вершину.
7. Пусть в пирамиде выполняется одно из следующих условий:
А) все боковые ребра образуют с плоскостью основания равные углы;
Б) длины всех боковых ребер равны.
Тогда вершина пирамиды проецируется в центр окружности, описанной около основания пирамиды.
8. Пусть в пирамиде выполняется одно из следующих условий:
А) все боковые грани образуют с плоскостью основания равные углы;
Б) длины всех апофем боковых граней равны.
Тогда вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.
III. Тела вращения.
Прямым круговым цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через одну из его сторон.
Прямым круговым конусом называется тело, полученное вращением прямоугольного треугольника вокруг оси, содержащей его катет.
Тело, полученное в результате вращения полукруга вокруг диаметра, называется шаром. Поверхность, образуемая при этом, называется сферой.
|
|
|
IV. Основные формулы стереометрии.
1. Произвольная призма. (  - боковое ребро;
- боковое ребро;  - периметр основания;
- периметр основания;  - площадь основания;
- площадь основания;  - высота;
- высота;  - периметр перпендикулярного сечения;
- периметр перпендикулярного сечения;  - площадь перпендикулярного сечения;
- площадь перпендикулярного сечения;  - площадь боковой поверхности;
- площадь боковой поверхности;  - объем):
- объем):

| 
| 
|
2. Прямая призма: 
3. Прямоугольный параллелепипед (  - его измерения,
- его измерения,  - диагональ):
- диагональ):

| 
| 
|
4. Куб (  - ребро):
- ребро):  и
и  .
.
5. Произвольная пирамида

| Правильная пирамида 
|
6. Произвольная усеченная пирамида (  ,
,  - площади оснований,
- площади оснований,  - высота):
- высота):
 .
.
7. Правильная усеченная пирамида (  ,
,  - периметры оснований,
- периметры оснований,  - апофема):
- апофема):
 .
.
8. Цилиндр (  -радиус основания):
-радиус основания):
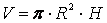
| 
|
9. Конус (  -образующая):
-образующая):

| 
|
10. Усеченный конус (  ,
,  - радиусы оснований,
- радиусы оснований,  - образующая):
- образующая):

| 
|
11. Шар, сфера (  - радиус шара,
- радиус шара,  - площадь сферической поверхности).
- площадь сферической поверхности).

| 
|
12. Шаровой сегмент (  - высота сегмента).
- высота сегмента).

| 
|
13. Шаровой сектор:
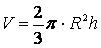 .
.
|
|
|


