Контрольные задачи к разделу 1

300. Точечные заряды q ₁=20 мкКл, q ₂= —10 мкКл находятся на расстоянии d =5 см друг от друга. Определить напряженность поля в точке, удаленной на r ₁=3 см от первого и на r ₂=4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд q =l мкКл.

301. Три одинаковых точечных заряда q ₁= q ₂= q₃ =2 нКл находятся в вершинах равностороннего треугольника со сторонами а =10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.

302. Два положительных точечных заряда q и 9 q закреплены на расстоянии d =100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

303. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Шарики погружают в масло. Какова плотность r масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков r_о=1,5 10³ кг/м³, диэлектрическая проницаемость масла e=2,2.

304. Четыре одинаковых заряда q ₁= q ₂= q ₃= q ₄=40 нКл закреплены в вершинах квадрата со стороной а =10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.

305. Точечные заряды q ₁=30 мкКл и q ₂= —20 мкКл находятся на расстоянии d =20 см друг от друга. Определить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние r ₁=30 см, а от второго —на r ₂=15 см.

306. В вершинах правильного треугольника со стороной а =10см находятся заряды q ₁=10 мкКл, q ₂=20 мкКл и q ₃=30 мкКл. Определить силу F, действующую на заряд q ₁ со стороны двух других зарядов.

307. В вершинах квадрата находятся одинаковые заряды q ₁= q ₂= q ₃= q ₄=8 10^-10 Кл. Какой отрицательный заряд q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

308. На расстоянии d =20 см находятся два точечных заряда: q ₁= —50 нКл и q ₂=100 нКл. Определить силу F, действующую на заряд q₃ = —10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

309. Расстояние d между двумя точечными зарядами q ₁=2 нКл и q ₂=4 нКл равно 60 см. Определить точку, в которую нужно поместить третий заряд q ₃ так, чтобы система зарядов находилась в равновесии. Определить заряд q ₃ и его знак. Устойчивое или неустойчивое будет равновесие?

310. Тонкий бесконечный прямолинейный стержень несет равномерно распределенный заряд t=0,1 мкКл/м. На расстоянии d =0,4 м от стержня находится точечный заряд q =0,01 мкКл. Определить напряженность Е электрического поля в точке, расположенной на одинаковом расстоянии от стержня и заряда d ₁ = 0,2 м.

311. Два параллельные бесконечные прямолинейные стержня заряжены с линейными плотностями t₁=+1 мкКл/м и t₂= —2 мкКл/м. Расстояние между ними равно d =0,5 м. Определить напряженность Е электрического поля, создаваемого стержнями в точке, находящейся на расстоянии d ₁=1 м от каждого из стержней.

312. Две бесконечные прямолинейные параллельные нити находятся на расстоянии d =0,5 м друг от друга. Линейные плотности электрического заряда на них составляют t₁=3мкКл/м и t₂ = —2 мкКл/м. Найти силу, действующую на единицу длины нитей.

313. Две бесконечные параллельные прямолинейные нити расположены на расстоянии d =0,1 м. Линейные плотности электрического заряда на них составляют t₁=t₂=10 мкКл/м. Определить напряженность Е электрического поля, создаваемого нитями в точке, находящейся на расстоянии d ₁=0,1 м от каждой из нитей.

314. Бесконечный прямолинейный тонкий стержень несет равномерно распределенный заряд с линейной плотностью t=0,5 мкКл/м. В точку А, удаленную от стержня на расстояние а =20 см, помещен точечный электрический заряд. В результате напряженность поля в точке В, находящейся на одинаковых расстояниях от точки А и от стержня, равных 10 см, оказалась равной нулю. Найти величину заряда.

315. С какой силой на единицу длины отталкиваются две одноименно заряженные бесконечные параллельные прямолинейные нити, если линейная плотность заряда на них составляет t=0,2 мкКл/м, а расстояние между нитями равно d =5 см.

316. Сила, действующая на точечный заряд q = —20 мкКл со стороны двух бесконечных прямых параллельных нитей, заряженных с одинаковой линейной плотностью t=0,1 мкКл/м, равна 10 мкН. Найти расстояние между нитями, если оно совпадает с расстоянием от заряда до каждой из нитей.

317. На расстоянии R =10 см от каждой из двух бесконечных прямолинейных нитей, заряженных положительно с одинаковыми линейными плотностями, находится точечный электрический заряд q =0,05 мкКл. Определить линейную плотность заряда на нитях, если модуль силы, действующей на заряд равен F =15 мН. Расстояние между нитями d =10 см.

318. Точечный заряд q= 10 нКл находится на расстоянии d =1,5 м от каждой из двух параллельных прямолинейных нитей, заряженных с одинаковой линейной плотностью t=0,01 мкКл/м. Определить силу, действующую на заряд, если расстояние между нитями d ₁=0,5 м.

319. На расстоянии R =10 см от бесконечной прямолинейной нити находится точечный заряд q = —20 мкКл. Линейная плотность заряда на нити t=0,2 мкКл/м. Определить напряженность Е электрического поля в точке, находящейся на одинаковом расстоянии 5см от нити и заряда.

320. На двух концентрических сферах радиусом R и 2 R равномерно распределены заряды с поверхностными плотностями s₁ и s₂, соответственно. Используя теорему Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I (0< r < R), II (R £ r <2 R) и III (r ³2 R). Принять s₁=4s, s₂=s, 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r _o, и указать направление вектора Е для значений s=30 нКл/м², r _o=1,5 R. 3) построить график E (r).

321. См. условие задачи 320. Принять s₁=s, s₂= — s; s=0,1 мкКл/м², r _o=3 R.

322. См. условие задачи 320. Принять s₁= —4s, s₂=s; s=50 нКл/м², r _o=1,5 R.

323. См. условие задачи 320. Принять s₁= —2s, s₂=s; s=0,1 мкКл/м², r _o=3 R.

324. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями s₁ и s₂, соответственно. Плоскости ортогональны оси Х и пересекают её в точках х=0 и х= а (а >0).

1) Используя теорему Гаусса и принцип суперпозиции электрических полей, найти выражение Е (x) напряженности электрического поля в трех областях: I (x<0), II (0<x< a) и III (x> a). Принять s₁=2s, s₂=s, 2) вычислить напряженность Е поля в точке, расположенной слева от плоскостей (x<0), и указать направление вектора Е; 3) построить график Е (х).

325. См. условие задачи 324. Принять s₁= —4s, s₂=2s; s=40 нКл/м², точку расположить между плоскостями (x=0,5 a).

326. См. условие задачи 324. Принять s₁=s, s₂= —2s; s=20 нКл/м², точку расположить справа от плоскостей (x=1,5 a).

327. На двух коаксиальных бесконечных цилиндрах радиусами R и 2 R равномерно распределены заряды с поверхностными плотностями s₁ и s₂, соответственно. 1) Используя теорему Гаусса, найти зависимость Е (r)напряженности электрического поля от расстояния r от общей осидля трех областей: I (0< r < R), II (R < r <2 R) и III (r>2 R). Принять s₁=—2s, s₂=s, 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r ₀, и указать направление вектора Е для значений s=50 нКл/м², r _o=1,5 R; 3) построить график E (r).

328. См. условие задачи 327. Принять s₁=s, s₂=—s; s=60 нКл/м², r _o=3 R.

329. См. условие задачи 327. Принять s₁= —s, s₂=4; s=30 нКл/м², r _o=4 R.

330. Два точечных заряда q ₁=6 нКл и q ₂=3 нКл находятся на расстоянии d =60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

331. Электрическое поле создано заряженным проводящим шаром, потенциал j которого 300 В. Под действием электрического поля шара заряд q =0,2 нКл перемещается вдоль прямой, проходящей через центр шара, причём начальная точка 1 находится на расстоянии 2 R от центра шара, а конечная точка 2 – на расстоянии 4 R (R -радиус шара). Определить работу сил поля по перемещению заряда q =0,2 мкКл из точки 1 в точку 2.

332. Электрическое поле создано зарядами q ₁=2мкКл и q ₂= — 2 мкКл, находящимися в точках А и В соответственно (АВ = а =10 см). Точка С находится на прямой АС ^ АВ (АС =2 а). Точка D находится на продолжении отрезка АВ (АD =3 а, ВD =2 а). Определить работу сил поля, совершаемую при перемещении заряда q =0,5 мкКл из точки С в точку D.

333. Две параллельные заряженные плоскости, поверхностные плотности заряда которых s₁=2 мкКл/м² и s₂= —0,8 мкКл/м², находятся на расстоянии d =0,6 см друг от друга. Определить разность потенциалов U между плоскостями.

334. Диполь с электрическим моментом р =100 пКл м свободно установился в электрическом поле напряженностью Е =200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол a=180°.

335. Четыре одинаковых капли ртути, заряженных до потенциала j=10 В, сливаются в одну. Каков потенциал j₁ образовавшейся капли?

336. Тонкий стержень согнут в кольцо радиусом R =10 см. Он равномерно заряжен с линейной плотностью заряда t=800 нКл/м. Определить потенциал j в точке, расположенной на оси кольца на расстоянии h =10 см от его центра.

337. Поле образовано точечным диполем с электрическим моментом р =200 пКл м. Определить разность потенциалов U между двумя точками, расположенными на оси диполя симметрично относительно его центра, на расстоянии r =40 см от центра диполя.

338. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой t=20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r ₁=8 см и r ₂=12 см.

339. Тонкое кольцо равномерно заряжено с линейной плотностью заряда t=200 пКл/м. Определить потенциал j поля в центре кольца.

340. Пылинка массой т =0,2 г, несущая на себе заряд q =40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U =200 В пылинка имела скорость v =10 м/с. Определить скорость v _o пылинки до того, как она влетела в поле.

341. Электрон, обладавший кинетической энергией T =10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U =8 В?

342. Найти отношение скоростей ионов Cu⁺⁺ и K⁺, прошедших одинаковую разность потенциалов.

343. Электрон с энергией T =400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R =10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = — 10 нКл.

344. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v =10⁵ м/с. Расстояние между пластинами d =8 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда s на пластинах.

345. Пылинка массой т =5 нг, несущая на себе N =10 электронов, прошла в вакууме ускоряющую разность потенциалов U =1MB. Какова кинетическая энергия T пылинки? Какую скорость v приобрела пылинка?

346. Какой минимальной скоростью v _min должен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала j=400 В металлического шара? Протон движется по прямой, проходящей через центр шара из точки, удалённой на расстояние r =4 R от центра шара (R -радиус шара).

347. В однородное электрическое поле напряженностью Е =200 В/м влетает (вдоль силовой линии) электрон со скоростью v _o=2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

348. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (t=10 нКл/м). Электрон движется перпендикулярно к этой линии. Определить кинетическую энергию T ₂ электрона в точке находящейся на расстоянии a от линии, если в точке, находящейся на расстоянии 3 a, его кинетическая энергия T ₁=200 эВ.

349. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом j₁=100 В электрон имел скорость v ₁=6 Мм/с. Определить потенциал j₂ точки поля, дойдя до которой электрон потеряет половину своей скорости.

350. Конденсаторы емкостью C ₁=5 мкФ и C ₂=10 мкФ заряжены до напряжений U ₁=60 В и U ₂=100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.

351. Конденсатор емкостью C ₁=10 мкФ заряжен до напряжения U =10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью C ₂=20 мкФ.

352. Конденсаторы емкостями C ₁=2 мкФ, C ₂=5 мкФ и C₃ =10 мкФ соединены последовательно и находятся под напряжением U =850 В. Определить напряжение и заряд на каждом из конденсаторов.

353. Два конденсатора емкостями C ₁=2 мкФ и C ₂=5 мкФ заряжены до напряжений U ₁=100 В и U ₂=150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

354. Два одинаковых плоских воздушных конденсатора емкостью C =100 пФ каждый соединены в батарею последовательно. Определить, на сколько (D C) изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

355. Два конденсатора емкостями C ₁=5 мкФ и C ₂=8 мкФ соединены последовательно и присоединены к батарее с ЭДС E=80 В. Определить заряды q ₁ и q ₂ конденсаторов и разности потенциалов U ₁ и U ₂ между их обкладками.

356. Плоский конденсатор состоит из двух круглых пластин радиусом R =10 см каждая. Расстояние между пластинами d =2 мм. Конденсатор присоединен к источнику напряжения U =80 В. Определить заряд q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик — воздух; б) диэлектрик — стекло.

357. Два металлических шарика радиусами R ₁=5 см и R ₂=10 см имеют заряды q ₁=40 нКл и q ₂= — 20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.

358. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d ₁=0,2 см и слоем парафина толщиной d ₂=0,3 см. Разность потенциалов между обкладками U =300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.

359. Плоский конденсатор с площадью пластин S =200 см²каждая заряжен до разности потенциалов U =2 кВ. Расстояние между пластинами d =2 см. Диэлектрик — стекло. Определить энергию W поля конденсатора и объемную плотность энергии w поля.

360. Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r =4 кОм. Амперметр показывает силу тока I =0,3 А, вольтметр — напряжение U =120 В. Определить сопротивление R катушки. Определить относительную погрешность e, которая будет допущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.

361. ЭДС батареи E=80 В, внутреннее сопротивление r =5 Ом. Внешняя цепь потребляет мощность P =100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.

362. От батареи, ЭДС которой E=600 В, требуется передать энергию на расстояние l =1 км. Потребляемая мощность P =5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d =0,5 см.

363. При внешнем сопротивлении R ₁=8 Ом сила. тока в цепи I ₁=0,8 А, при сопротивлении R ₂=15 Ом сила тока I ₂=0,5 А. Определить силу тока I _кз короткого замыкания источника ЭДС.

364. ЭДС батареи E=24 В. Наибольшая сила тока, которую может дать батарея, I _max=10 А. Определить максимальную мощность P _mах, которая может выделяться во внешней цепи.

365. Аккумулятор с ЭДС E=12 В заряжается от сети постоянного тока с напряжением U =15 В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление r =10 Ом.

366. От источника с напряжением U =800 В необходимо передать потребителю мощность Р =10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?

367. При включении электромотора в сеть с напряжением U =220 В он потребляет ток I =5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.

368. В сеть с напряжением U =100 В подключили катушку с сопротивлением R ₁=2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U ₁=80 В. Когда катушку заменили другой, вольтметр показал U ₂=60 В. Определить сопротивление R ₂ другой катушки.

369. ЭДС батареи E=12 В. При силе тока I =4 А КПД батареи h=0,6. Определить внутреннее сопротивление r батареи.

370. За время t =20 с при равномерно возраставшей силе тока от нуля до некоторого максимума в проводнике сопротивлением R =5 Ом выделилось количество теплоты Q=4 кДж. Определить скорость нарастания силы тока, если сопротивление проводника R =5 Ом.

371. Сила тока в проводнике изменяется со временем по закону I = I _oexp(-a t), где I _o=20 А, а a=10² с^-1. Определить количество теплоты, выделившееся в проводнике сопротивлением R = 10 Ом за время t =10^-2 с.

372. Сила тока в проводнике сопротивлением R =10 Ом за время t =50 с равномерно нарастает от I ₁=5 А до I ₂=10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.

373. В проводнике за время t =10 с при равномерном возрастании силы тока от I ₁=1 А до I ₂=2 А выделилось количество теплоты Q=5 кДж. Найти сопротивление R проводника.

374. Сила тока в проводнике изменяется со временем по закону I = I _o sinw t. Найти заряд q, проходящий через поперечное сечение проводника за время t, равное половине периода T, если амплитуда силы тока I _o=10 А, циклическая частота w=50p с^-1.

375. За время t =10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q=40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопротивление R =25 Ом.

376. За время t =8 с при равномерно возраставшей силе тока в проводнике сопротивлением R =8 Ом выделилось количество теплоты Q=500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.

377. Определить количество теплоты Q, выделившееся за время t =10 с в проводнике сопротивлением R =10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I ₁=10 А до I ₂=0 А.

378. Сила тока в цепи изменяется по закону I = I_o sinw t. Определить количество теплоты, которое выделится в проводнике сопротивлением R =10Ом за время, равное четверти периода (от t ₁= 0 до t ₂= T /4, где T =10 с). Амплитуда силы тока I _o=5А.

379. Сила тока в цепи изменяется со временем по закону I = I_o exp(-a t). Определить количество теплоты, которое выделится в проводнике сопротивлением R =20 Омза время, в течение которого ток уменьшится в е (2,718) раз. Коэффициент a принять равным 2 10^-2 с^-1, I _o=5А.

380. Два шарика массой т =1 г каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити l =10см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол a==60°?

381. Расстояние между зарядами q ₁=100 нКл и q ₂= —50 нКл равно d =10 см. Определить силу F, действующую на заряд q₃ =1 мкКл, отстоящую на r ₁=12 см от заряда q ₁ и на r ₂=10 см от заряда q ₂.

382. Тонкий стержень длиной l = 10 см равномерно заряжен с линейной плотностью t=1,5 нКл/см. На продолжении оси стержня на расстоянии d =12 см от его конца находится точечный заряд q =0,2 мкКл. Определить силу взаимодействия заряженного стержня и точечного заряда.

383. Две бесконечные параллельные прямые тонкие проволоки заряжены с одинаковой линейной плотностью. Вычислить линейную плотность t заряда на каждой из них, если напряженность поля в точке, находящейся на расстоянии r =0,5 м от каждой проволоки, Е =2 В/см, а расстояние между проволоками равно 0,5 м.

384. С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости с одинаковой поверхностной плотностью заряда s=2 мкКл/м²?

385. Какую ускоряющую разность потенциалов U должен пройти электрон, чтобы получить скорость v =8 Мм/с?

386. Заряд равномерно распределен по бесконечной плоскости с поверхностной плотностью s=10 нКл/м². Определить разность потенциалов двух точек поля, одна из которых находится на плоскости, а другая удалена от нее на расстояние а =10 см.

387. Электрон с начальной скоростью v =3 Мм/с влетел в однородное электрическое поле напряженностью Е =150 В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Определить: 1) силу, действующую на электрон; 2) ускорение, приобретаемое электроном; 3) скорость электрона через t =0,1 мкс.

388. К батарее с ЭДС E=300 В включены два плоских конденсатора емкостями С ₁=2 пФ и С ₂=З пФ. Определить заряд q и напряжение U на пластинках конденсаторов при последовательном и параллельном соединениях.

389. Конденсатор емкостью С ₁=600 пФ зарядили до разности потенциалов U ₁=1,5 кВ и отключили от источника напряжения. Затем к нему параллельно присоединили незаряженный конденсатор емкостью С ₂=400 пФ. Определить энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.

390. На концах медного провода длиной l =5 м поддерживается напряжение U =1 В. Определить плотность тока j в проводе.

391. Резистор сопротивлением R ₁=5 Ом, вольтметр и источник тока соединены параллельно. Вольтметр показывает напряжение U ₁=10 В. Если заменить резистор другим с сопротивлением R ₂=12 Ом, то вольтметр покажет напряжение U ₂=12 В. Определить ЭДС и внутреннее сопротивление источника тока. Током через вольтметр пренебречь.

392. Определить электрический заряд, прошедший через поперечное сечение провода сопротивлением R =3 Ом, при равномерном нарастании напряжения на концах провода от U ₁=2 В до U ₂=4 В в течение t =20 с.

393. Определить силу тока в цепи, состоящей из двух элементов с ЭДС E₁=l,6 В и E₂=1,2 В и внутренними сопротивлениями R ₁=0,6 Ом и R ₂=0,4 Ом, соединенных одноименными полюсами.

394. Гальванический элемент дает на внешнее сопротивление R ₁=0,5 Ом силу тока I ₁=0,2 A. Если внешнее сопротивление заменить на R ₂=0,8 Ом, то элемент дает силу тока I ₂=0,15 А. Определить силу тока короткого замыкания.

395. К источнику тока с ЭДС E=12 В присоединена нагрузка. Напряжение U на клеммах источника стало при этом равным 8 В. Определить КПД источника тока.

396. Внешняя цепь источника тока потребляет мощность Р =0,75 Вт. Определить силу тока в цепи, если ЭДС источника тока E=2 В и внутреннее сопротивление R =1 Ом.

397. Какая наибольшая полезная мощность Р _max может быть получена от источника тока с ЭДС E=12 В и внутренним сопротивлением R =1 Ом?

398. При выключении источника тока сила тока в цепи убывает по закону I = I _оexp(-a t) (I _о=10А, a=5 10² с^-1). Определить количество теплоты, которое выделится в резисторе сопротивлением R =5 Ом после выключения источника тока.

399. Сила тока в проводнике сопротивлением R =25 Ом возрастает в течение времени D t =2 с по линейному закону от I _о=0 до I =5 А. Определить количество теплоты Q₁ выделившееся в этом проводнике за первую секунду и Q₂- за вторую.

Электромагнетизм

Основные понятия и формулы

Связь магнитной индукции В магнитного поля напряженностью Н

,

где m — относительная магнитная проницаемость среды; m_o —магнитная постоянная. В вакууме m= 1.

Закон Био—Савара—Лапласа

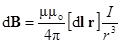или ,

где d B —магнитная индукция поля, создаваемого элементом провода длиной d l с током I; r —радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; a — угол между радиусом-вектором и направлением тока в элементе провода d l.

Магнитная индукция в центре кругового тока

,

где R — радиус кругового витка.

Магнитная индукция на оси кругового тока

,

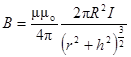где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока

,

где r _о — расстояние от оси провода до точки, в которой определяется магнитная индукция.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: