 |
Модель случайной структуры
|
|
|
|
Композиционные материалы
Композиционный материал - неоднородный сплошной материал, состоящий из двух или более компонентов, среди которых можно выделить армирующие элементы, обеспечивающие необходимые механические характеристики материала, и матрицу (или связующее), обеспечивающую совместную работу армирующих элементов.
Композиты состоят из полимерной, металлической, углеродной, керамической или др. основы (матрицы), армированной наполнителями из волокон, нитевидных кристаллов, тонкодиспeрсных частиц и др.
Механическое поведение композита определяется соотношением свойств армирующих элементов и матрицы, а также прочностью связи между ними. Эффективность и работоспособность материала зависят от правильного выбора исходных компонентов и технологии их совмещения, призванной обеспечить прочную связь между компонентами при сохранении их первоначальных характеристик.
В результате совмещения армирующих элементов и матрицы образуется комплекс свойств композита, не только отражающий исходные характеристики его компонентов, но и включающий свойств, которыми изолированные компоненты не обладают. В частности, наличие границ раздела между армирующими элементами и матрицей существенно повышает трещиностойкость материала, и в композитах, в отличие от металлов, повышение статической прочности приводит не к снижению, а, как правило, к повышению характеристик вязкости разрушения.
Преимущества композиционных материалов:
высокая удельная прочность
высокая жёсткость(модуль упругости130…140 ГПа)
высокая износостойкость
высокая усталостная прочность
из КМ возможно изготовить размеростабильные конструкции
|
|
|
Причём, разные классы композитов могут обладать одним или несколькими преимуществами. Некоторых преимуществ невозможно добиться одновременно.
Недостатки композиционных материалов
Большинство классов композитов (но не все) обладают недостатками:
высокая стоимость
анизотропия свойств 
Сферопластики представляют собой легкий, высокопрочный водо- и маслобензостойкий материал плотностью от 500 до 700 кг/м3 на основе высокопрочных эпоксидных связующих и полых микросфер. Сферопластики являются трудновоспламеняемым, невзрывоопасным, нетоксичным продуктом. Диапазон рабочих температур от –150 до +150°С. Глубоководные сферопластики выдерживают давление водяного столба до 12 км. Водопоглощение материала – нулевое.
Эти свойства определяют сферы применения. Будучи заливочным малоусадочным материалом, сферопластики способны заполнять оснастку любой конфигурации.
Сферопластики получают на специальных промышленных установках непрерывного или периодического действия. Изделия и конструкции из сферопластиков получают методами свободной заливки, литья под давлением, прессования, шпательной укладки, напыления.
Материал проверен временем в нефтегазовой, судостроительной промышленности, в авиации, строительстве, электротехнике.
Модель случайной структуры
Пусть в некоторой области V с границей Г задана представительная реализация некоторой случайной структуры композита, обладающей свойствами статистической однородности и эргодичности. Считаем, что включения геометрически подобны и состоят из F однородных фаз; включения имеют случайные структуры и, например, одинаковую геометрическую форму и ориентацию в однородной матрице предварительной области композита V. Выполняются условия идеального контакта на межфазных поверхностях.
Глобальная r и локальная для k-го включения 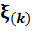 координаты произвольной точки из представительной области композита V связаны соотношением
координаты произвольной точки из представительной области композита V связаны соотношением
|
|
|
 +
+  ,
,  =
= 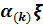 , (2.1)
, (2.1)
Нормированная локальная координата
𝞷≡  (r-
(r- 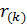 ), (2.2)
), (2.2)
где 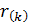 – радиус-вектор центра k-го включения в глобальной системе координат,
– радиус-вектор центра k-го включения в глобальной системе координат,  - коэффициент подобия k-го включения, k=
- коэффициент подобия k-го включения, k= 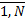 .
.
Введем в рассмотрение типовое нормированное включение 𝞾: объем 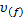 произвольной f -й фазы этого включения равен среднему арифметическому значению от объемов
произвольной f -й фазы этого включения равен среднему арифметическому значению от объемов  всех N включений из представительной области V,
всех N включений из представительной области V,
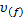 =
= 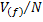 , (2.3)
, (2.3)
Где 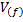 =
=  - объем области
- объем области 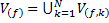 f -й фазы включений в V. Поскольку объем
f -й фазы включений в V. Поскольку объем  области f -й фазы k-го включения выражается как
области f -й фазы k-го включения выражается как
 =
=  (2.4)
(2.4)
Через коэффициент подобия  k-го включения и объем
k-го включения и объем 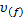 f -й фазы нормированного включения 𝞾, следовательно, после исключения из (2.3) и (2.4) величины
f -й фазы нормированного включения 𝞾, следовательно, после исключения из (2.3) и (2.4) величины 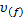 следует равенство
следует равенство
 =1, (2.5)
=1, (2.5)
где показатель степени β равен 1,2 или 3 соответственно для слоистого, однонаправленного волокнистого или гранулированного композитов.
Поскольку все включения геометрически подобны, поэтому, чтобы задать относительное расположение фаз внутри них, достаточно задать это расположение в нормированном включении 𝞾 через совокупность индикаторных функций фаз
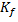 (𝞷)=
(𝞷)= 
В локальной системе координат 𝞷, центр которой поместим в центр области этого включения
𝞾≡  , (2.6)
, (2.6)
Где 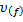 - область f -й фазы F -фазного включения 𝞾.
- область f -й фазы F -фазного включения 𝞾.
Индикаторная функция 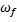 (r) f -й фазы включений в представительной области композита V задана в виде
(r) f -й фазы включений в представительной области композита V задана в виде
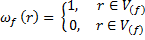 , (2.7)
, (2.7)
Где 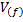 - область f -й фазы включений в области V. Относительное объемное содержание f -й фазы включений в представительной области V композита есть
- область f -й фазы включений в области V. Относительное объемное содержание f -й фазы включений в представительной области V композита есть
 , (2.8)
, (2.8)
Где оператор осреднения по представительному объему
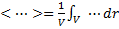 . (2.9)
. (2.9)
Для случая r 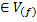 функция
функция  связана с нормированной индикаторной функцией
связана с нормированной индикаторной функцией 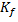 (𝞷) в локальной системе координат 𝞷 равенством
(𝞷) в локальной системе координат 𝞷 равенством
 (𝞷)𝟂(r)
(𝞷)𝟂(r)
Благодаря геометрическому подобию всех включений в представительной области композита V; индикаторная функция составных включений
𝟂(r)≡  .
.
Относительное объемное содержание составных волокон в композите
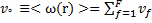 (2.11)
(2.11)
с учетом равенства (2.8).
Представительные реализации статистически однородных эргодических тензорных полей упругих С(r) и пьезоупругих e(r) свойств, диэлектрической проницаемости λ(r), коэффициентов температурных напряжений β(r) и пироэлектрических постоянных π(r) композита в области V заданы разложениями
|
|
|
C(r) =  e(r) =
e(r) = 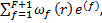 λ(r) =
λ(r) = 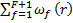
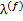 , (2.12)
, (2.12)
β(r) = 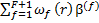 , π(r)=
, π(r)= 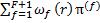
через поля индикаторных функций (2.7) и тензоры соответствующих пьезомеханических свойств: 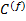 ,
, 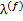 ,
, 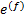 ,
, 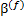 , и
, и 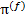 фаз композита. Поля индикаторных функций
фаз композита. Поля индикаторных функций  комплексно учитывают случайное взаимное расположение, форму и размеры включений в объеме композита и расположение фаз, например, внутри составных включений.
комплексно учитывают случайное взаимное расположение, форму и размеры включений в объеме композита и расположение фаз, например, внутри составных включений.
При рассмотрении композита со случайными свойствами фаз включений считаем, что пьезомеханические свойства некоторого целого числа 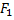 фаз варьируются пропорционально единому случайному коэффициенту χ, а упругие свойства остальных F-
фаз варьируются пропорционально единому случайному коэффициенту χ, а упругие свойства остальных F- 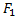 фаз включений и матрицы – детерминированы, где 0
фаз включений и матрицы – детерминированы, где 0 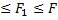 . Например, представительную реализацию поля упругих свойств C(r) в области V возможно представить разложением
. Например, представительную реализацию поля упругих свойств C(r) в области V возможно представить разложением
C(r)= 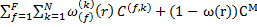
или
C(r)= 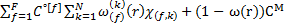 (2.13)
(2.13)
Через индикаторную функцию включений
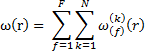
и индикаторные функции f -й фазы k-го включения
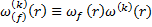 ,
,
Где использованы индикаторные функции  для области f -й фазы включений
для области f -й фазы включений 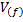 и
и
 (2.14)
(2.14)
Для области k-го включения 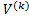 в области композита V;
в области композита V;  - тензор упругих свойств матрицы,
- тензор упругих свойств матрицы,  -номинальные значения тензора упругих свойств f -й фазы, коэффициенты
-номинальные значения тензора упругих свойств f -й фазы, коэффициенты
 (2.15)
(2.15)
Задают пропорциональное отклонение действительных значений компонент тензора упругих свойств
 (2.16)
(2.16)
Для f -й фазы k-го включения от соответствующих номинальных значений компонент тензора  f -й фазы.
f -й фазы.
|
|
|


